2.1.3 Распространение световых лучей в оптических волокнах

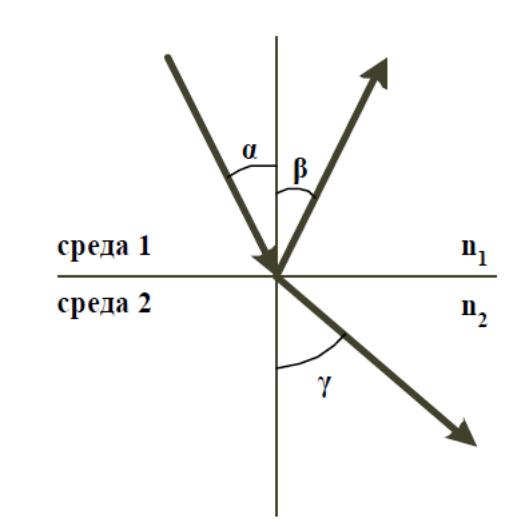
Как известно среда, у которой показатель преломления больше, называется оптически более плотной, в противном случае – менее плотной, поэтому при падении луча света на границу раздела таких сред в общем случае появляются отражения и преломления волны, причем в соответствии с законом Снеллиуса углы падения α, отражения β и преломления γ связаны следующими соотношениями:

1. α = β – закон отражения;

2. n₁ sin α = n₂ sin γ – закон преломления.

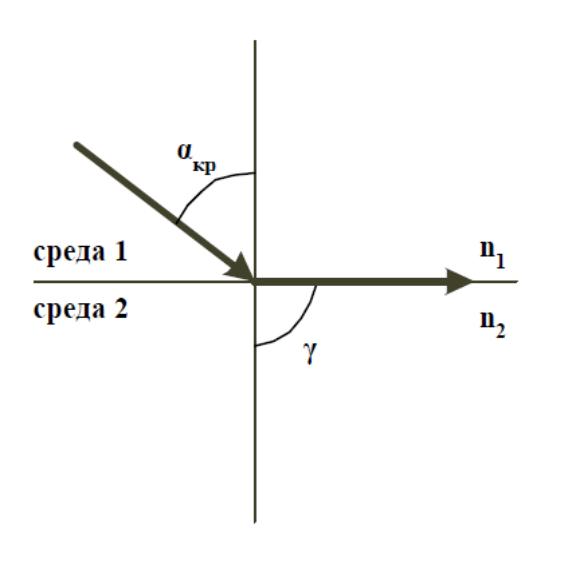
Если луч переходит из оптически более плотной среды в менее плотную n₁ > n₂ , то γ > α. Путем увеличения угла падения можно достичь состояния, при котором преломленный луч будет скользить по границе раздела сред, не переходя в другую среду (рисунок 2.1).

Угол падения при котором имеет место данный эффект, называется критическим углом α_акр. полного внутреннего отражения. Для критического угла α_кр имеет место следующее отношение [16]:

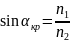, (2.1)

_где α_{кр – критический угол;}

n₁ – показатель преломления первой среды;

n_{2 – показатель преломления второй среды.}

Очевидно, что для всех углов падения, больших критического (α > α_кр), будут иметь место только отражения, а преломления будут отсутствовать. Это явление называется полным внутренним отражением. Поскольку вся мощность светового луча практически полностью возвращаются в область боле плотной среды, на этом эффекте основан принцип передачи оптического излучения по ОВ. Если угол падения на границу раздела меньше критического угла падения то при каждом внутреннем отражении часть энергии рассеивается в виде преломленного луча, что приводит в конечном итоге к затуханию света [5].

а) б)

Рисунок 2.1 – Преломление света на границе двух сред с различным показателем преломления: а) угол падения меньше критического угла; б) угол падения равен критическому углу

Лучи, траектории которых полностью лежат в оптически более плотной среде, называются направляемыми. Поскольку энергия в направляемых лучах не рассеивается наружу, такие лучи могут распространяться на большие расстояния

В общем случае ОВ состоит из сердечника, по которому происходит распространение световых волн и оболочки, предназначенной с одной стороны, для создания лучших условий отражения на границе раздела «сердечник – оболочка», а с другой стороны – для снижения излучения энергии в окружающее пространство. С целью повышения прочности и тем самым надежности волокна поверх оболочки, как правило, накладывается защитное покрытие (рисунок 2.2).

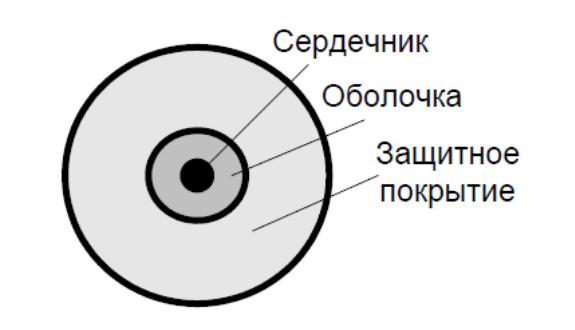
Рисунок 2.2 – Конструкция оптического волокна

Основными факторами, влияющими на характер распространения света в волокне, наряду с длиной волны излучения, являются: геометрические параметры волокна; затухание; дисперсия.

Рассмотрим геометрические параметры волокна

Относительная разность показателей преломления. Волокно состоит из сердцевины и оболочки. Оболочка окружает оптически более плотную сердцевину, являющуюся светонесущей частью волокна. Будем обозначать через n₁ и n₂ показатели преломления сердцевины и оболочки, соответственно. Один из важных параметров, который характеризует волокно, это - относительная разность показателей преломления Δ [16]:

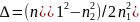, (2.2)

где Δ – относительная разность показателей преломления;

n₁ – показатель преломления первой среды;,

n_{2 – показатель преломления второй среды.}

Числовая апертура. Угол между оптической осью и одной из образующих светового конуса – лучей, падающих в торец ОВ, для которых в дальнейшем выполняется условие полного внутреннего отражения, носит название апертура ОВ (рисунок 2.3). Физически апертура характеризует эффективность ввода оптического излучения в ОВ, а для ее числовой оценки используется понятие числовой апертуры (NA).

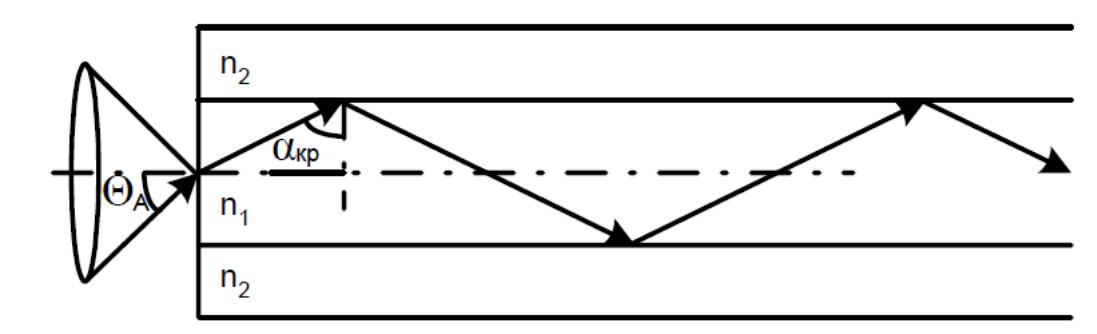
Рисунок 2.3 – Распространение света в оптическом волокне

Числовая апертура связана с максимальным углом Θ_A вводимого в волокно излучения из свободного пространства, при котором свет испытывает полное внутреннее отражение и распространяется по волокну, формулой [16]:

NA = sin θ_А, (2.3)

где NA– числовая апертура;

θ_А – угол вводимого, в волокно излучения из свободного пространства, при котором свет испытывает полное внутреннее отражение;

Для обеспечения условия полного внутреннего отражения при распространении световых лучей необходимо обеспечить ввод излучения в торец волокна под углом меньше или равным θ_А

Числовая апертура для ступенчатого волокна равна [16]:

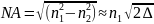, (2.4)

Из последнего выражения видно, что с увеличением разности показателей преломления сердечника и оболочки значение NA возрастает и, следовательно, улучшается эффективность ввода излучения в ОВ.

Нормированная частота. Другим важным параметром, характеризующим волокно и распространяющийся по нему свет, является нормированная частота V, которая определяется как [16]

V = π⋅d⋅NA/λ, (2.5)

где d – диаметр сердцевины волокна, нм;

NA – числовая апертура;

λ – длина волны излучения, нм.

Номенклатура мод. При более строгом рассмотрении процесса распространения света по волокну следует решать волновые уравнения Максвелла. Именно в этой трактовке лучи ассоциируются с волнами, причем различные типы волн – решения уравнений – называются модами. Сами моды обозначаются буквами Е и/или Н с двумя индексами n и m (Е_nm и Н_nm). Индекс n - характеризует азимутальные свойства волны (число изменений поля по окружности), a m - радиальные (число изменений поля по диаметру). По оптическому волокну распространяются только два типа волн: симметричные (Е_оm и Н_оm), у которых только одна продольная составляющая, и несимметричные (смешанные) (Е_nm и Н_nm), у которых имеется две продольные составляющие. При этом, если преобладает продольная составляющая электрического поля – Е_Z, то волна обозначается EH_nm, а если преобладает продольная составляющая магнитного поля – Н_Z, то волна называется НЕ_nm. Сопоставляя волновую теорию с геометрической оптикой, следует отметить, что симметричные моды Е и Н соответствуют меридиональным лучам, несимметричные моды Е_nm и Н_nm – косым лучам [16].

По волокну могут распространяться как только одна мода - одномодовый режим, так и много мод – многомодовый режим. Многомодовый или одномодовый характер идущего по волокну света коренным образом влияет на дисперсию, а следовательно, и на пропускную способность волокна. Расчет на основе уравнений Максвелла позволяет найти простой критерий распространения одной моды:

V < 2,405, (2.6)

где число 2,405 – значение аргумента (х) функции Бесселя I₀(x) при ее первом нулевом значении.

Кривые функций Бесселя I₀(x) выглядят как затухающие синусоидальные колебания. Это математическая функция для описания электрического поля в цилиндрических волноводах, таких как коаксиальные кабели, полые трубки или волоконные световоды. Следует отметить, что нормированная частота явно зависит от длины волны света.

Количество мод. Если при V < 2,405 может распространяться только одна мода, то с ростом V количество мод начинает резко расти, причем новые типы мод «включаются» при переходе V через определенные критические значения.

Длина волны отсечки – минимальная длина волны, при которой волокно поддерживает только одну распространяемую моду. Этот параметр характерен для одномодового волокна. Если рабочая длина волны меньше длины волны отсечки, то имеет место многомодовый режим распространения света. В этом случае появляется дополнительный источник дисперсии - межмодовая дисперсия, ведущий к уменьшению полосы пропускания волокна. Значение длины волны отсечки легко определяется из условия одномодовости [16]

где λ_мин – длина волны отсечки, нм;

Различают волоконную длину волны отсечки и кабельную длину волны отсечки. Первая соответствует слабо напряженному волокну. На практике же волокно помещается в кабель, который при прокладке испытывает множество изгибов. Кроме этого, сильные искривления волокон происходят при их укладке в сплайс-боксах. Все это ведет к подавлению побочных мод и смещению кабельной длины волны отсечки в сторону коротких длин волн.