I Термохимия.

1) Термодинамические системы (открытая, закрытая, изолированная). Параметры и функции состояния системы. Энтальпия, энтропия, энергия Гиббса. |

Термодинамическая система – тело или совокупность тел, мысленно выделенная из окружающей среды. Открытая – обменивается с окружающей средой веществом и энергией. Закрытая – только энергией, изолированная – ни веществом, ни энергией. Параметры состояния системы – T,P,V, концентрация и т.д. Функции системы: внутренняя энергия U, энтальпия H, энтропия S, энергия Гиббса G.(функции, т.к. зависят от параметров системы).Тепловой эффект в ходе реакции – изменение энтальпии или энтальпия процесса. dH=dU+PdV. S – мера неупорядоченности системы(количественная мера беспорядка). Возможность протекания реакции характеризуется изменением энтропии. S=klnW, где k – пост. Больцмана, W-число микросостояний в макросистеме. Энергия Гиббса – изобарно-изотермический потенциал. dG=dH-TdS. dG характеризует возможность самопроизвольного протекания процесса.dG<0 – протекает, >0, самопроизвольно не протекает.

2) Тепловые эффекты химических реакций. Эндо- и экзотермические процессы. Закон Гесса и его следствия. Стандартная энтальпия образования вещества. |

3) Закон Гесса. Следствия закона Гесса: связь энтальпии химической реакции со стандартными энтальпиями образования, сгорания или разрыва связей для исходных веществ и продуктов реакции. Стандартные энтальпии образования и сгорания химических соединений. |

4) Закон Гесса для теплового эффекта физико-химического процесса. Следствия закона Гесса: связь энтальпии химической реакции со стандартными энтальпиями образования, сгорания или разрыва связей для исходных веществ и продуктов реакции.|

5) Стандартные энтальпии термодинамических процессов: энтальпия образования, сгорании. Энтальпии растворения, нейтрализации. Энергия связи. |

Тепловой эффект химической реакции или изменение энтальпии системы вследствие протекания химической реакции — отнесенное к изменению химической переменной количество теплоты, полученное системой, в которой прошла химическая реакция и продукты реакции приняли температуру реагентов. Стандартная энтальпия образования dH⁰_обр – тепловой эффект реакции (ТЭР) образования одного моля в-ва из простых в-в, его составляющих, находящихся в устойчивых стандартных состояниях. dH⁰_обрf простого в-ва = 0(относится к агрегатному состоянию, устойчивому при T=298K). Стандартная энтальпия сгорания dH⁰_сгор – ТЭР сгорания одного моля в-ва до высших оксидов. Стандартная энтальпия разрыва связи(называется также Е_св ) dH⁰_св – энергия, поглощаемая при разрыве 1 моля связей двух атомов находящихся в газообразном состоянии при 298К. Энтальпия растворения складывается из теплоты разрушения кристаллической решетки (dH⁰_реш >0) и теплоты гидратации(сольватации для неводных растворов) (dH⁰_гидр <0). Энтальпия растворения может иметь как +, так и -. Стандартная энтальпия нейтрализации dH⁰_нейтр – энтальпия реакции взаимодействия сильных кислот и оснований с образованием 1 моля воды. Стандартная энтальпия реакции dH⁰ – тепловой эффект реакции определённого числа молей реагентов задаваемого уравнением реакции при стандартных условиях. Экзотермическая реакция – реакция, сопровождающаяся выделением теплоты (dH <0). Эндо – поглощением (dH⁰ >0). Закон Гесса – Тепловой эффект(энтальпия) реакции процесса зависит только от начального и конечного состояния системы и не зависит от пути перехода её из 1 состояния в другое. Следствия: 1)энтальпия реакции равна разности сумм энтальпий образования конечных и начальных участников реакции с учётом их стехиометрических коэффициентов (домножение суммы на коэффициент). dH⁰_реак = ΣdH⁰_{обр кон} -ΣdH⁰_{обр нач}. 2)Энтальпия реакции равна разности сумм энтальпий сгорания начальных и конечных реагентов с учётом их стехиометрических коэффициентов. dH⁰_реак = ΣdH⁰_{сгор кон} -ΣdH⁰_{сгор нач}.3) Энтальпия реакции равна разности сумм энергий связей E_св исходных и конечных веществ с учётом их стехиометрических коэффициентов. dH_реак = ΣЕ_исх –ΣЕ_прод.4) Энтальпия образования в-ва равна энтальпии разложения его до простых в-в с обратным знаком. 5) Энтальпия гидратации равна разности энтальпия растворения безводной соли и кристаллогидрата. dH⁰_гидр =dH⁰_{раств б/с}-dH⁰_{раств крист} 6) Закон Гесса и его следствия распространяются и на другие функции состояния(S⁰ dG⁰ ). dФ⁰=ΣdФ_{обр пр} –ΣdФ_{обр исх}. Закон Гесса позволяет обращаться с термохимическими уравнениями как с алгебраическими. Энергия связи – энергия связанной системы каких-либо частиц (например, атома), равная работе, которую необходимо затратить, чтобы разложить эту систему на бесконечно удаленные друг от друга и не взаимодействующие между собой составляющие ее частицы.

6) Термодинамический критерий осуществимости процесса. Энергия Гиббса. Энтальпийный и энтропийный факторы и их роль в экзо- и эндотеримческих реакциях.|

7) Энергия Гиббса как критерий осуществимости химических реакций. Анализ уравнения Гиббса для экзо- и эндотермических реакций при ΔS > 0 и ΔS < 0. |

8)Факторы, определяющие направление протекания химических реакций, анализ уравнения Гиббса для замкнутой системы. Изотерма Вант-Гоффа. |

Энергия Гиббса – изобарно-изотермический потенциал. dG=dH-TdS. dG характеризует возможность самопроизвольного протекания процесса.dG<0 – протекает, >0, самопроизвольно не протекает. В случае экзотермических реакций при dS<0 следует понижать T. Для эндотермических реакций, осуществимых за счёт энтропийного фактора и только при dS>0 необходимы T>1000К. При комнатной температуре обычно TdS невелико и изменение энтальпии больше, нежели энтропии. Поэтому большинство реакций, протекающих при комнатной Т, экзотермичны. dH образования и реакции составляют 80-800 кДж/моль(редко больше 4000 и меньше 40). dH сгорания всегда <0 и составляет тысячи кДж/моль. Энтальпия фазовых превращений обычно < энтальпии реакций. Парообразования – несколько десятков, кристаллизации и плавления ~5-25 кДж/моль. dH_T=dH⁰+dC_p*dT, где dC_p – изменение теплоёмкости системы. Если фазового перехода не произошло, то dC_p=0. Энтропия индивидуальных веществ всегда>0.(от десятков до сотен кДж/моль). Наибольшие значения dS имеют фазовые переходы. Если реакция экзотермична, то знак dG определяет энтальпийный фактор. Также при низких Т вклад энтропийного фактора мал и о направлении реакции можно судить по dH. Эндотермические реакции идут тем успешнее, чем выше Т и если происходит фазовый переход (тогда TdS относительно велико). Для оценки осуществимости процесса используют, однако, не dG, а dG⁰. Однако эта величина не может использоваться как критерий осуществимости процесса с большим возрастанием энтропии(Напр. Фазовые переходы и реакции термического разложения). Такие реакции могут быть осуществлены при условии, что Т>(dH/dS). Однако стоит заметить, что значения dG⁰>>0 и dG⁰<<0 говорят нам о принципиальной возможности протекания реакции. Обычно порогом реакции считают dG⁰>25 кДж/моль (до этого значения процесс можно осуществить). Изотерма Вант-Гоффа(для 8 вопроса). Чтобы определить dG в нестандартных условиях используют уравнение зависимости dG от концентрации и температуры. (Нест. Условия –это, например, концентрация >1 моль и T не 298К, что повышает/понижает реакционную способность в-ва). Тогда dG_i=dG⁰_i+RT*ln(a_i), где a_i-активная концентрация в-ва. Для перехода из первого состояния во второе можно записать dG₂-dG₁=dG_1-2=dG⁰_1-2+RT*ln(a₁/a₂). Для произвольной химической реакции: aA+bB=mM+nN записывается: dG=dG⁰+RT*ln(a_M^m*a_Nⁿ/a_A^a*a_B^b) (т.к. согласно закону Гесса dG⁰=ΣdG_{обр пр} –ΣdG_{обр исх}). Если концентрации равновесные(dG=0), то dG⁰=-RT*ln(a_M^m*a_Nⁿ/a_A^a*a_B^b). Выражение поз логарифмом называется константа равновесия К. dG⁰=-RT*ln(К). Окончательно, dG=-RT*lnK+ RT*ln(a_M^m*a_Nⁿ/a_A^a*a_B^b). Если реакция проходит в гальваническом элементе, то dG=-A_max=-nFE (n-число моль-электронов, переходящих от окислителя к восст-лю, F-число Фарадея, Е-разность потенциалов [В]).

II Кинетика

1) Понятие скорости химических реакций. Зависимость скорости химических реакции от концентраций реагирующих веществ в гомогенных системах. Кинетическое уравнение. Константа скорости химической реакции.

2) Понятие скорости химических реакций. Порядок и молекулярность химических реакций.

Кинетика отвечает на вопросы: какие факторы влияют на скорость реакции, каков путь реакции, каковы промежуточные продукты? Она изучает скорость ХР в зависимости от концентрации реагирующих в-в, влияния катализаторов и других факторов, механизмы их протекания. Скорость реакции определяется по изменению концентраций реагирующих в-в во времени. Скорость реакции aA+bB=dD определяется по соотношению v_i=+-(dc_i/n*dt)(производная концентрации по времени). Влияние концентрации на скорость реакции. Для обратимой гомогенной реакции скорость прямой и обратной реакции равна. Для H2+I2=2HI: v=k[H2]*[I2]=k[HI]^2 (Закон действующих масс), в скобках стоят мгновенные молярные концентрации. K-константа скорости реакции, зависящая только от природы реагентов и температуры. В случае гетерогенной реакции(реакции в-в в нескольких агрегатных состояниях) в уравнение ЗДМ входит лишь концентрация газообразных в-в. Обычно реакция протекает через многостадийные процессы. В таких случаях пользуются кинетическим уравнением: v=+-1/n’(dc_i/dt)=k_ic_iⁿ, где n’- стехиометрический коэффициент, n – порядок реакции. Формальным порядком реакции называется показатель степени в кинетическом уравнении реакции, определяемый экспериментально. Прологарифмировав это уравнение получаем линейную форму lgv=lgk+n*lgc, где n=tgφ. Также порядок реакции может быть определён следующим способом – интегрированием кинетического уравнения. -dc/dt=kcⁿ. Тогда мы получаем зависимость с от времени. n=1: ln(c₀/c_t)=kt; n=2: 1/c_t-1/c₀=kt; n=3: 1/c_t²-1/c₀²=kt. Тогда, если построить графики lnc,1/c,1/c² от t, они будут иметь вид прямой. Метод определения порядка реакции – метод избытка реагента. aA+bB=dD. Сначала избыток в-ва А, потом B, в итоге получаем, что v=K*c_A^m*c_Bⁿ. Порядок реакции равен m+n. Молекулярность-число молекул, принимающих участиве в элементарном акте химического превращения. Бывает 1,2 и 3-молекулярные. В реакции молекулярность – сумма стехиометрических коэффициентов. Она часто не совпадает с порядком реакции, т.к. стех. Ур-ние не отражает механизма реакции. Типы ХР. 1)Параллельные(в-ва одновременно реагируют в нескольких направлениях). V=k₁[A]+k₂[B]. Скорость реакции определяется самой быстрой реакцией. V1/V2=k1/k2=const (Принцип независимости ХР).2)Последовательные(реакции с промежуточными стадиями). Константа скорости и скорость посл. Реакций определяется самой медленной реакцией. 3)Цепные(радикальные реакции, в кот. Превращение исходных в-в в продукты осуществляется путём многократного чередования свободных радикалов или атомов) Скорость реакции резко возрастает. 4)Фотохимические(под действием света, каждый квант вызывает превращение одной молекулы(закон Эйнштейна), количество продуктов пропорционально интенсивности падающего света и времени его воздействия(Закон Гершеля и Дрепера). 2 вида фхр: где свет – возбудитель реакции, и где свет – условее протекания реакции.

3) Влияние температуры на скорость химических реакций. Уравнение Аррениуса, физический смысл входящих в него величин. Энергия активации.

4) Влияние температуры на скорость химических реакций. Уравнение Аррениуса. Понятие об энергии активации. Катализ, принцип действия катализаторов.

Скорость ХР сложным образом зависит от температуры. Строгим и физически обоснованным является зависимость k от T в виде уравнения Аррениуса : k=A*exp(-E_a/RT), где А – предэкспоненциальный множитель или фактор частоты, R – универсальная газовая постоянная, E_а-энергия активации, Т – абсолютная температура(К). Энергия, которую надо сообщить молю в-ва, чтобы все его молекулы стали активными в данной реакции называют энергией активации(E_a). Чем больше ЭА, тем медленнее протекает реакция. Если 50<E_a<100 (кДж/моль), то при изменении температуры на 10 градусов, скорость изменится в 2-4 раза(Вант-Гофф). Если известны 2 способа протекания одной реакции, то Е_а=(R*T₁*T₂*ln(k₁/k₂)/T₂-T₁). Предэкспоненциальный множитель А характеризует общее число соударений. Для простых реакция А=Z, для реакций со сложными в-вами A=Z*P, Р(стерический фактор, принимает значения от 1 до 10^-9) учитывает то, что для взаимодействия необходимо правильное взаимное расположение молекул. Тогда уравнение Аррениуса принимает вид: k=ZP*exp(-E_a/RT)(*). Размерность предэкспоненты та же, что и у константы скорости. K=v/cⁿ. Из (*) видно, что есть 2 способа ускорения реакции – увеличение Т и уменьшение E_a. Последнее осуществляется с помощью катализаторов. Само явление – катализ. Различают гомогенный и гетерогенный катализ (в зависимости от фазы катализатора). Обычная реакция: A+B->A-B(активированный комплекс)->AB. С катализатором: A+K->A-K->AK; AK+B->K-A-B->AB+K. Катализатор не тратится. Увеличение скорости: v_k/v=(exp(E_a-E_a.K.)/RT). */ На пути реакции A+B=D лежит энергетический барьер, который необходимо перейти, чтобы произошла реакция(Активированный комплекс)./*

5) Химическое равновесие и его константа. Факторы, влияющие на смещение химического равновесия. Принцип Ле-Шателье.

Чаще всего приходится иметь дело с обратимыми реакциями. aA+bB=cC+dD. Для прямой и обратной реакций: v_пр=k_пр[A]^a[B]^b, v_обр=k_обр[C]^c[D]^d.(в квадратных скобках – мгновенные концентрации). В состоянии равновесия v_пр=v_обр. Константа равновесия К=k_пр/k_обр= [C]^c[D]^d/[A]^a[B]^b. При заданной Т К будет постоянной. dG⁰=-RT*lnK. К выражается и через парциальные давления(K_p). N2+3H2=2NH3: K_p=P²_NH3/(P_N2*P³_H2), K_c=(c_NH3)^2/(c_N2*c³_H2). K_c=K_p*(RT)^dn, где dn – изменение числа молей в реакции. Принцип Ле-Шателье. Если на систему оказывать внешнее воздействие, то в системе возникают процессы, уменьшающие внешнее воздействие. Изменение Т. К=k_пр/k_обр= A*exp(-(E_a.пр-Е_а.обр)/RT)=А*exp(-dH/RT). Т.е. чем больше dH, тем больше влияние Т. Охлаждение благоприятствует экзотермическому процессу. Нагревание – эндотермическому. Изменение Р. Смещает равновесие реакций, если dn!=0. Повышение Р смещает равновесие в сторону процесса, при котором уменьшается V. Изменение С. Избыток исходного в-ва смещает равновесие влево, продукта – вправо. При этом К=const(т.к. зависит от Т). Введение катализатора. Не вызывает смещение равновесия(т.к. катализатор ускоряет реакцию).

Химические источники тока

1) Устройство, принцип действия и схема обозначений типичного химического источника электрической энергии (на примере гальванического элемента Даниэля-Якоби). Каков механизм появления двойного электрического слоя и электродного потенциала? |

2) Гальванический элемент Даниэля-Якоби: схема, процессы, происходящие на электродах, суммарный электрохимический процесс. Уравнение Нернста для

каждого электрода и для гальванического элемента в целом. Роль солевого мостика в гальваническом элементе. |

3) Стандартный электродный потенциал. Зависимость электродного потенциала от концентрации потенциалопределяющих ионов и температуры. Уравнение Нернста для отдельного электрода в нестандартных условиях. |

4) Стандартный электродный потенциал, измерение стандартного электродного потенциала. Устройство стандартного водородного электрода. Составьте схему для определения стандартного электродного потенциала медного электрода. |

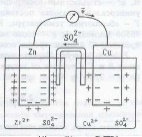В основе электрохимии лежат ОВР, т.е. ХР, сопровождающиеся переходом электронов от одного атома(восстановителя) к другому(окислителю). ХИТ – устройства, получающие электроэнергию, используя ОВР. Устройство ГЭ Даниэля-Якоби. 2 сосуда, в которых электрод, помещённый в раствор электролита, соединёны солевым мостиком (или пористой перегородкой). Солевой мостик – стеклянная трубка, заполненная р-ром электролита, катионы и анионы которого одинаково подвижны(обычно KCl). Соединив электроды проводником первого рода, начнётся ОВР, о чём говорит возникновение ЭДС. В основе ГЭ Д-Я реакция: CuSO₄+Zn<->Cu+ZnSO₄. Запиисывается ГЭ так: (-)Zn|Zn²⁺||Cu²⁺|Cu(+). Слева записывается анод(электрод, на кот. Проходит процесс окисления(отдача е)), справа – катод(электрод, на кот. Проходит процесс восстановление). Направление тока от анода к катоду. Реакции на электродах. Электродные реакции проходят на границе раздела «электрод-металл». На аноде: Zn_тв-2e=Zn²⁺_р, вследствие чего раствор обогащается катионами Zn²⁺. На Катоде: Cu²⁺_p+2e=Cu_тв­, в следствие чего р-р обогащается анионами SO₄^2-. Тогда к аноду движутся аноды, а к катоду – катионы. Электродный потенциал. В системе Ме-электролит возможен переход катионов металла в раствор или из раствора на поверхность металла(в зависимости от природы Ме и электролита). Эти процессы определяются соотношением энтальпии отрыва иона от крист. Решетки (dH_реш) и энтальпии сольватации этого иона Mⁿ⁺_aq(dH_сольв). На границе фаз Ме-электролит устанавливается равновесие: M+aq <->ne+Mⁿ⁺*aq. Если С ионов Ме в р-ре меньше равновесной, то возникает отрицательный заряд на границе Ме по отношению к р-ру(и Ме -> в раствор). Если С > равновесной, то происходит переход ионов из р-ра на Ме, заряжженный положительно(относительно р-ра). Вследствие этого на границе двух сред возникает электродный(гальвани-) потенциал(т.е. двойной электрический слой на границе двух фаз). Уравнение Нернста. (для металлического)Е_{окисл.ф./восст.ф.}=Е_{0 ок.ф./в.ф.}+(0,059/n)lg(Ameⁿ⁺). Получение оного: Для произвольной химической реакции: aA+bB=mM+nN записывается: dG=dG⁰+RT*ln(a_M^m*a_Nⁿ/a_A^a*a_B^b), причём dG=-A_max=-qE=-n_eFE, т.е.: - n_eFE= -n_eFE₀+RT*ln(a_M^m*a_Nⁿ/a_A^a*a_B^b), отсюда E=E₀-(RT/nF)ln(a_M^m*a_Nⁿ/a_A^a*a_B^b)=E₀+(0,059/n)*ln (a_A^a*a_B^b / a_M^m*a_Nⁿ). Причём активность твёрдых в-в = 1. Уравнение Нернста для отдельного электрода условились писать для процесса восстановления(+ne);Роль солевого мостика в ГЭ. Поддержание баланса отрицательных и положительных ионов в растворе. Стандартный электродный потенциал. (v_i-стех. Коэффициент) Абсолютное значение потенциала на границе раздела двух сред измерить нельзя, но можно измерить разность электродных потенциалов элементов, то есть ЭДС, возникающую в контуре. Если же ЭП одного из электродов выбрать эталонным и принять его Е за 0, то СЭП будет равен ЭДС контура. Такой эталонный электрод – водородный электрод. Устройство: платиновый электрод, покрытый платиновой чернью(мелкодисперсной платиной), погруженный в р-р серной кислоты с а=1 моль/л, обдувается струёй газообразного Н под давлением 1 атм=1,03*10⁵Па. Реакция: Н₂<-> 2Н⁺+2e. Схема определения СЭП: (-)Pt, H₂|2H⁺||Mⁿ⁺|M(+) Если СЭП<0, то металл записывается слева( и электрод с металлом – анод).

5) Таблица стандартных электродных потенциалов для окислительно-восстановительных систем. Металлический электрод, уравнение Нернста для металлического электрода. |

Металлический электрод – металл, погруженный в раствор своей соли M|Mⁿ⁺, например, цинковый или медный. Е_{окисл.ф./восст.ф.}=Е_{0 ок.ф./в.ф.}+(0,059/n)lg(Ameⁿ⁺)

6) Электроды 1-го и 2-го рода на примере медного и хлорсеребряного электродов. Уравнение Нернста для них. Почему электроды 2-го рода можно использовать в качестве электродов сравнения? |

7) Электроды сравнения: водородный, хлорсеребряный, стеклянный. Устройство, уравнение Нернста. Почему электроды 2-го рода можно использовать в качестве электродов сравнения? |

8) Стеклянный электрод: устройство, уравнение Нернста. |

Электроды 1-го рода: 1) электроды, состоящие из элементарного в-ва, находящегося в контакте с раствором, содержащим его собственные ионы (например, металлический(медный. Cu²⁺_p+2e=Cu_тв­, в следствие чего р-р обогащается анионами SO₄^2-, а на поверхности электрода оседает металлическая медь. Е_{окисл.ф./восст.ф.}=Е_{0 ок.ф./в.ф.}+(0,059/n)lg(Ameⁿ⁺)) или газовый). 2) Редокс-электроды. Состоят из инертного по отношению к данному электролиту проводника первого рода(платина, графит), погруженного в раствор, в котором находятся одновременно окисленная и восстановленная формы потенциалопределяющего в-ва. Пример: Pt|Sn⁴⁺,Sn²⁺; Pt|Fe³⁺,Fe²⁺. Уравнение Нернста: E_{ок.ф./вост.ф.}=E_{0.ок.ф./вост.ф.} +(0,059/dn)lg(a_ок.ф./а_{восст.ф}). Окисленная форма – та, где заряд больше. Электроды 2-го рода. Металлические пластины, покрытые слоем труднорастворимой соли того же металла и опущенные в раствор, содержащий анион этой соли. Его потенциал определяется активностью аниона в р-ре. Хлорсеребряный электрод. Ag|AgCl|Cl^-. (серебряный проводник покрыт слоем AgCl, который погружен в насыщенный р-р KCl. Ag⁺+e=Ag⁰. E_Ag+/Ag=E_0.Ag+/Ag+0,059*lg(a_Ag+). Но т.к. активность связана с произведением растворимости(ПР) хлорида серебра(ПР_AgCl=a_Ag+*a_Cl-), то E_Ag+/Ag=E_0.Ag+/Ag+0,059*lg(ПР_AgCl)-0,059*lg(a_Cl-­). =>E_хсэ =E_хсэ-0,059*lg(a_Cl-­­). Здесь ионы хлора потенциалопределяющие. AgCl_тв+е=Ag⁺+Cl^-. Таким образом, Электроды 2-го рода можно использовать в кач-ве электродов сравнения, т.к. они обратимы по отношению к аниону, активность которого можно поддерживать постоянной, что приводит к постоянству электродного потенциала. Стеклянный электрод. Стеклянный электрод – электрод для определения концентрации H⁺ (pH) относится к ионоселективным(мембранным) электродам. Он состоит из стеклянного тонкостенного шарика(мембраны), припаянного к стеклянной трубке. В шарике – р-р HCl (a_H+=0,1 моль/л), в который опущен хлорсеребряный электрод. При погружении электрода в раствор с измеряемой C_H+ между мембраной и исследуемым в-вом возникает разность потенциалов(из-за процесса ионного обмена). Е_ст=Е_0.ст.+0.059*lg[H⁺]=Е_0.ст.-0.059*pH_внеш. Водородный электрод. Устройство: платиновый электрод, покрытый платиновой чернью(мелкодисперсной платиной), погруженный в р-р серной кислоты с а=1 моль/л, обдувается струёй газообразного Н под давлением 1 атм=1,03*10⁵Па. Реакция: Н₂<-> 2Н⁺+2e. Схема определения СЭП: (-)Pt, H₂|2H⁺||Mⁿ⁺|M(+) Если СЭП<0, то металл записывается слева( и электрод с металлом – анод). Дополнение. Концентрационный элемент – одинаковые электроды с разными активностями потенциалопределяющего иона. Существуют такще сухие элементы (батарейки) .

9) Аккумуляторы (на примере свинцового аккумулятора). Реакции на аноде и катоде, суммарная реакция в свинцовом аккумуляторе при его работе (разрядке) и зарядке. ЭДС свинцового аккумулятора (конечная формула с использованием активности серной кислоты и воды). |

Аккумулятор – обратимый гальванический элемент многоразового действия. При пропускании через них электрического тока(зарядке) аккумуляторы накапливают хим. Энергию, которую потом при работе(разрядке) отдают в виде электрической энергии. Наиболее распространённые - свинцовый(кислотный) и щелочной. Свинцовый аккумулятор. Активная масса анода – перфорированные свинцовые пластины, катода – диоксид свинца, впрессованный в свинцовые решётки. Электролит – раствор (35%) H₂SO₄. Схема: (-)Pb|PbSO₄|H₂SO₄|PbSO₄|PbO₂|Pb(+).При работе протекает реакции: (-)Pb+SO₄^2--2e=PbSO₄. E_0.PbSO4/Pb=-0,36B; (+) PbO₂+4H⁺+SO₄^2-+2e=PbSO₄+2H₂O. E_0.PbO2/PbSO4=1,69B. Суммарная реакция: Pb_тв+PbO_2.тв+2H₂SO₄  2PbSO_4тв+2H₂O. Уравнение Нернста записывается так(учитывая, что а_тв=1): Е= E_0.PbO2/PbSO4-E_0.PbSO4/Pb+0,059lg(a_H2SO4/a_H2O)=2.05+0,059lg(a_H2SO4/a_H2O) . В процессе работы аккумулятора концентрация кислоты падает, а следовательно, падает и ЭДС. Когда ЭДС достигает 1,85 В, аккумулятор считается разрядившимся. При более низкой ЭДС пластины покрываются тонким слоем PbSO₄ и и аккумулятор разряжается необратимо. Во избежание этого аккумулятор периодически подзаряжают. Дополнительно: щелочной железо-никелевый аккумулятор. Электролит – 20% КОН. Активная масса анода – губчатое железо, катода – гидроксид никеля. (-)Fe|Fe(OH)₂|KOH|Ni(OH)₂|Ni(OH)₃|Ni(+). Суммарная реакция: Fe+2Ni(OH)₃Fe(OH)₂+Ni(OH)₂. В уравнении Нернста стоят не активности, а ПР данных нерастворимых в-в. E=E_{0.Ni(OH)3/Ni(OH)2}-E_Fe(OH)2/Fe +(0.059/2)lg(ПР²_Ni(OH)3/(ПР²_Ni(OH)2*ПР_Fe(OH)2). Его преимущество – ЭДС не зависит от концентрации щёлочи.