3.4. Анализ процесса качения эластичного колеса по деформируемому грунту

Рассмотренный пример приближенного построения формы линии контакта эластичного колеса с грунтом показывает сложность задачи учета формы контакта и особенно эпюр нормальных и касательных напряжений при определении пара­метров качения колеса по грунту.

Воспользуемся известным понятием эквивалентного жесткого колеса, па­раметры поверхности контакта которого равновелики с эластичным колесом. Воз­можность такой замены была неоднократно подтверждена экспериментально.

При качении колеса с номинальным давлением воздуха в шине величина деформации шины мала по сравнению с деформацией грунта и характер взаимо­действия шины с деформируемым грунтом может быть описан зависимостями, аналогичными полученным для жесткого колеса, радиус которого г₀ равен радиусу эластичного колеса.

При прогибе шины более 7% от свободного диаметра, когда форма и разме­ры контакта меняются, радиус эквивалентного жесткого колеса определяется по следующей известной зависимости:

Положение точки А определяется пересечением линии действия реакции R, отстоящей от центра колеса на расстояние ОВ, с поверхностью эквивалентного коле­са. Расстояние ОВ определяется из уравнения силового равновесия колеса и равно:

3.5. Работа, затрачиваемая на деформацию грунта при колееобразовании

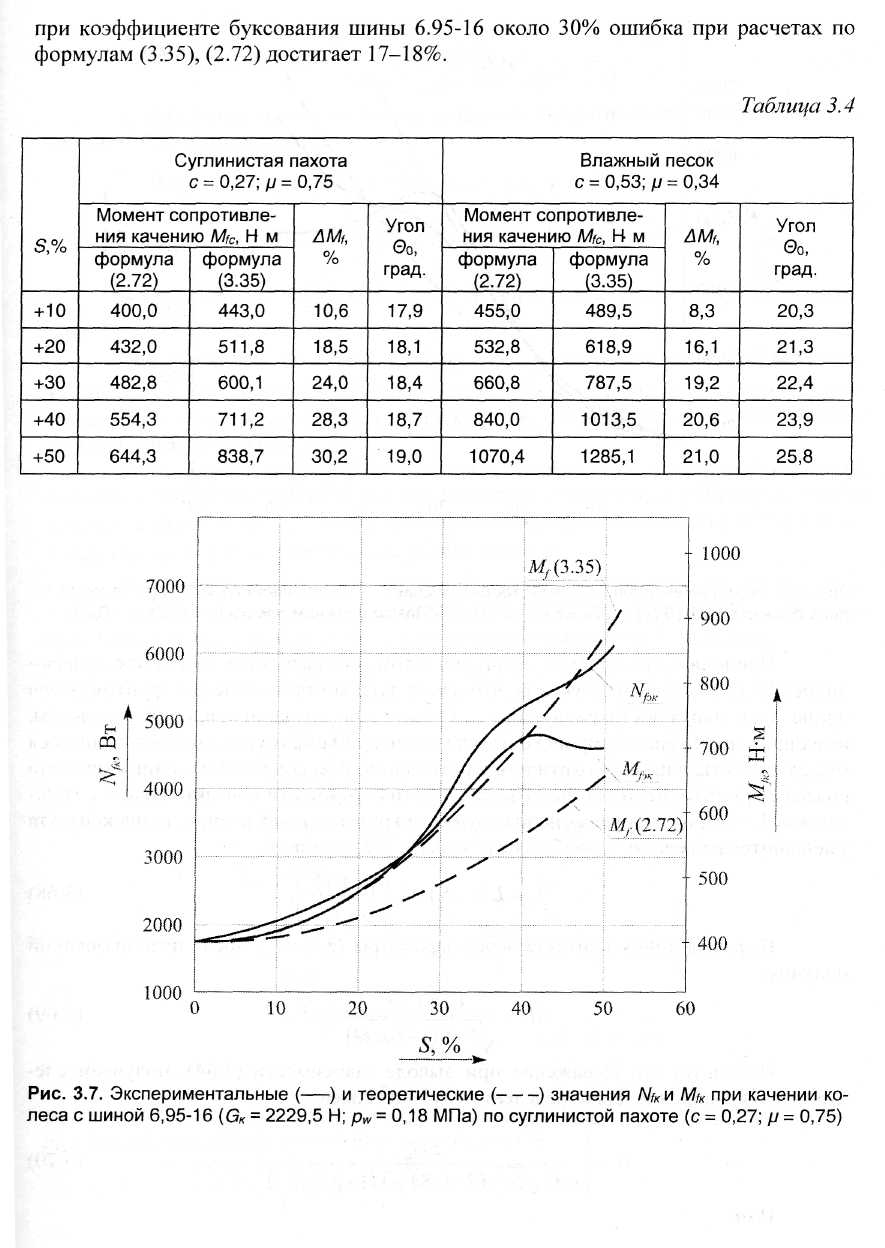
В ранее проведенных исследованиях отмечается, что при движении ко­леса происходит не только смятие грунта в вертикальном направлении, но и его пе­ремещение по горизонтали. Таким образом, необходимо учитывать траекторию частиц грунта при образовании колеи, что является сложной задачей, требующей применения методов механики грунтов, механики сплошных сред, решения крае­вых задач, определения перемещения частиц грунта по поверхности колеса и т. п. Несколько упрощает решение задачи принятие Ю.В. Пирковским и М.П. Чистовым допущения, что в свободном режиме качения колеса частицы грунта, контакти­рующие с его поверхностью, неподвижны относительно нее, т. е. их траектория имеет вид нормальной циклоиды. В результате были получены следующие выра­жения для момента сопротивления качению колеса в свободном режиме М_fc:

3.7. Влияние грунтозацепов при взаимодействии колеса с грунтом

Как отмечалось выше, наличие грунтозацепов на эластичном колесе приво­дит к расхождению экспериментальных и расчетных зависимостей по определению потерь мощности при качении колеса по грунту. Рассмотрим этот вопрос более подробно, используя расчетную схему на рис. 3.12, в которой учитывается криво-линейность зоны контакта колеса с грунтом. Полагаем, что форма линии контакта описывается системой уравнений (3.16), а сопротивление грунта смятию - выраже­нием (3.1).

Выразим глубину погружения i-той точки А колеса в грунт через текущие значения радиус-вектора r и полярного угла . Определим нормальные напряжения в точке А:

При отклонении формы линии контакта колеса с грунтом от окружности направление нормали в /-той точке контакта отклоняется от направления радиус-вектора г на угол .