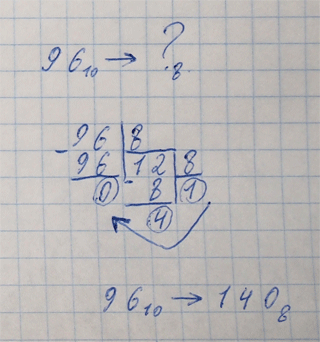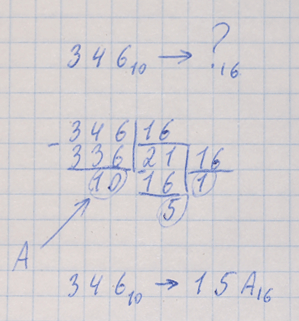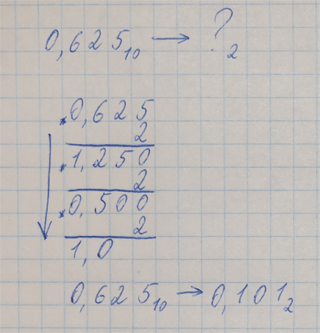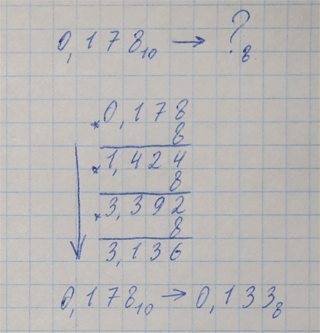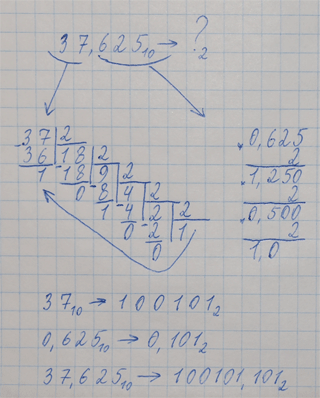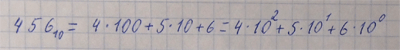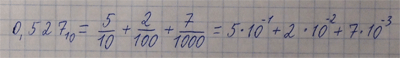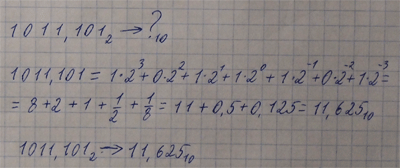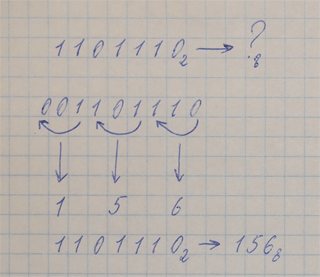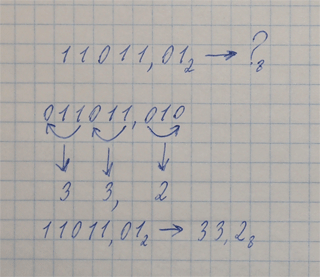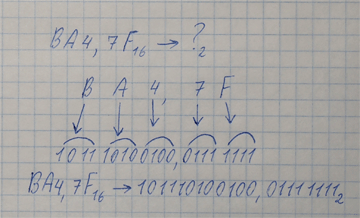Правило перевода дробных чисел

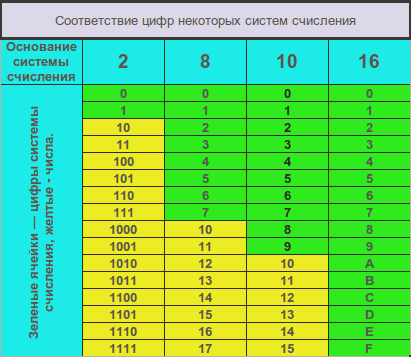
Это полная версия статьи о системах счисления и правилах перевода чисел, содержащая текст, иллюстрации и обучающее видео.

Общая информация о системах счисления

Если вам нужны именно правила перевода чисел, пропустите общую информацию.

Система счисления – это способ представления любого числа с помощью определенного набора символов, называемых цифрами. Основание системы счисления – это количество цифр, используемых в данной системе счисления.

Позиционными называются системы счисления, в которых значение цифры зависит от ее места (позиции) в записи числа. Непозиционными называются системы счисления, в которых значение цифры не зависит от ее места (позиции) в записи числа.

Позиционной является привычная для нас в повседневной жизни десятичная система счисления, в которой значение (вес) цифры зависит от ее позиции в записи числа. В числе 1111 одна и та же цифра 1 означает последовательно единицу, десяток, сотню, тысячу.

Все системы счисления, используемые в информатике (двоичная, восьмеричная, шестнадцатеричная и т. д.), являются позиционными. Это важно, т. к. правила образования чисел, перевода из одной системы в другую, выполнения арифметических операций во всех позиционных системах аналогичны.

Непозиционной системой счисления является, например, римская. Правила выполнения арифметических операций в непозиционных системах счисления совсем иные.

В 2-ной системе основание равно 2, т.е. используется всего 2 цифры - 0 и 1. В 8-ной основание равно 8, используются цифры от 0 до 7. В 16-ной системе основание равно 16, используются цифры от 0 до 15. Использование цифр 10, 11, 12, 13, 14, 15 в записи чисел неудобно, т. к. трудно отличить, например, цифру 12 от двух цифр – 1 и 2. Поэтому условились цифры от 10 до 15 обозначать латинскими буквами в порядке алфавита A, B, C, D, E, F.

Таблица соответствия цифр в различных системах счисления

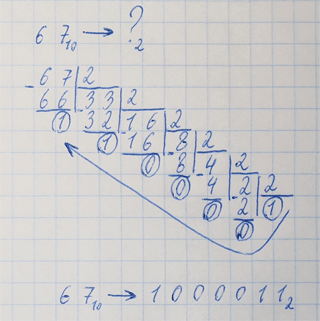
Перевод целого числа из 10-ной системы счисления в любую другую

Посмотрите обучающее видео или прочитайте правило перевода в виде текста ниже.

Чтобы перевести целое число Х из 10-ной системы в любую другую с основанием Q:

1. делим Х на Q, в результате чего получается целая часть частного и остаток (может быть равен нулю, если разделилось нацело).

2. если полученная целая часть частного меньше Q, переходим к шагу 3. Если равно или больше Q, снова делим целую часть частного на Q, как описано в шаге 1. Внимание: делится только целая часть, остаток в делении не участвует (он пригодится позже).

3. все полученные остатки и последняя целая часть частного (меньшая, чем Q) преобразуются в соответствии с таблицей перевода в цифры той системы счисления, в которую выполняется перевод. Иными словами, если, к примеру, при переводе в 16-ную систему у вас получился остаток 12, то его нужно преобразовать в 16-ную цифру С.

4. Получаем ответ. Его первая (старшая) цифра - последнее частное, а остальные - остатки от деления, записанные в порядке, обратном порядку их получения.

Пример 1:

Пример 2:

Пример 3:

Перевод правильной дроби из 10-ной системы счисления в любую другую

Смотрите видео или прочитайте правила в текстовом виде ниже.

Чтобы перевести правильную дробь X из 10-ной систему счисления в любую другую с основанием Q:

1. X умножаем на Q.

2. в полученном произведении целая часть (может быть равной нулю) преобразуется в цифру системы с основанием Q по таблице перевода цифр. Каждая из этих целых частей будет цифрой в ответе.

3. если дробная часть произведения равна нулю, переходим к шагу 4. Если не равна нулю, умножаем дробную часть произведения на Q, как написано в шагах 1 и 2. Обратите внимание: умножается только дробная часть, целая в умножении не участвует.

4. Получаем ответ: пишем "0,", а после десятичной запятой - преобразованные по таблице целые части произведений в порядке их получения (сверху вниз).

Внимание! Умножать можно либо до получения нуля в дробной части, либо пока не будет достигнута нужная точность (требуемое количество цифр после запятой). Следует учесть, что дробь, не периодическая в 10-ной системе счисления, может оказаться периодической в другой системе.

Пример 1:

Пример 2, перевод с точностью до 3-х знаков после запятой:

Перевод смешанных чисел (неправильных дробей) из 10-ной системы счисления в любую другую

Если число Х имеет целую и дробную часть, то переводим целую часть по правилу для целых чисел, а дробную (вместе с нулем и десятичной запятой "0,") по правилу для дробей. Потом к переведенной целой части "приклеиваем" справа переведенную дробную (убрав из нее "0,").

Пример 1:

Перевод числа (целого или дроби) из любой системы счисления в 10-ную

Воспользуйтесь обучающим видео. Текст правила дан ниже.

Чтобы перевести число из системы счисления с основанием Q в 10-ную:

1. Представляем число в виде полинома от основания системы счисления и вычисляем его значение. Полином - представление числа в виде суммы его цифр, умноженных на соответствующую степень основания системы счисления.

Внимание: цифры в полиномах и основание записываются в 10-ной системе счисления (переводим по таблице).

Примеры полиномов:

Пример 1:

Пример 2:

Пример 3:

Пример перевода чисел в 10-ную систему:

Перевод числа (целого или дроби) из 2-ной системы счисления в 8-ную и 16-ную

Используйте обучающее видео или текст правил перевода ниже.

Вообще, это правило работает для перевода из 2-ной системы счисления в любую, основание которой представляет собой целую степень двойки, но мы рассмотрим его на примере 8-ной и 16-ной.

Напомню: 8=2³, 16=2⁴.

Чтобы перевести число из 2-ной в 8-ную систему счисления:

1. Разбиваем 2-ное число на группы из трех цифр (триады). При разбиении двигаемся влево от запятой в целой части числа и вправо от запятой - в дробной части. Если цифр не хватает для того, чтобы заполнить самую левую или самую правую триады, то добавляем к числу незначащие нули. В целой части нули можно добавить слева, в дробной - справа.

Примечание: целая или дробная часть числа может быть равна нулю. В этом случае мы ничего с ней не делаем, т.к. ноль будет нулем в любой системе счисления.

2. С помощью таблицы перевода цифр заменяем каждую триаду 8-ной цифрой. В случае смешанного числа не забудьте про запятую, отделяющую целую часть от дробной. Ответ готов.

Чтобы перевести число из 2-ной в 16-ную систему счисления действуем точно так же, только разбивая двоичное число на группы из 4 двоичных цифр (тетрады).

Это сработает и для 4-ной системы, т.к. 4=2². В этом случае следует брать группы из двух двоичных цифр. В общем случае число разрядов (цифр) в группе равно степени двойки.

Пример 1:

Пример 2:

Пример 3:

Перевод числа из 8-ной и 16-ной систем счисления в 2-ную

Такой перевод выполняется обратно предыдущему случаю. Обучающее видео дано выше.

Рассмотрим для 8-ной системы счисления. Чтобы перевести 8-ное число в 2-ную систему счисления:

1. По таблице перевода цифр заменяем каждую 8-ную цифру триадой (группой из трех) 2-ных цифр. Если 8-ная цифра соответствует группе из двух 2-ных цифр (например, 3₈=11₂), то двоичная группа дополняется нулями слева так, чтобы получилось три двоичных цифры (011₂).

2. Если в целой части получившегося 2-ного числа есть крайние слева нули, убираем их. Так же поступаем с крайними нулями справа в дробной части.

При переводе из 16-ной системы счисления в 2-ную действуем точно так же, только заменяем каждую 16-ную цифру группой из четырех двоичных цифр, дополняя ее при необходимости нулями слева.

Это правило сработает при переводе в 2-ную из любой системы счисления, основание которой представляет собой целую степень числа 2. Количество цифр в группе равно показателю степени.

Пример:

Перевод числа (целого или дроби) из 8-ной в 16-ную и обратно

Такой перевод выполняется через 2-ную систему: 8-ное число сначала переводится в 2-ную, а потом из 2-ной в 16-ную. Из 16-ной в 8-ную переводим аналогично через 2-ную.

А чтобы отработать перевод чисел из одной системы счисления в другую на практике можно отправиться к тренажерам на перевод чисел. :-)

• 1

• 2

• 3

• 4

• 5

Категория: Информатика | Добавил: Орк (30.01.2012)

Просмотров: 25980 | Комментарии: 1 | Теги: системы счисления, обучающее видео, информатика | Рейтинг:4.0/4

Всего комментариев: 1