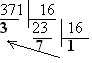В шестнадцатеричной системе счисления основание системы равно 16, т.е. для записи чисел используется 16 символов: цифры от 0 до 9 и далее буквы латинского алфавита от A до F

Ниже представлена таблица соответствия кодов чисел четырех систем счисления. Двоичный код числа представлен 8 разрядами - 1 байтом.

10-ая	8-ая	2-ая	16-ая	10-ая	8-ая	2-ая	16-ая
0	0	00000000	0	8	10	00001000	8
1	1	00000001	1	9	11	00001001	9
2	2	00000010	2	10	12	00001010	A
3	3	00000011	3	11	13	00001011	B
4	4	00000100	4	12	14	00001100	C
5	5	00000101	5	13	15	00001101	D
6	6	00000110	6	14	16	00001110	E
7	7	00000111	7	15	17	00001111	F

 

Для записи 1 цифры шестнадцатеричного числа в двоичной системе счисления требуется 4 разряда.

Алгоритм перевода чисел из 2-ой в 16-ую систему счисления

При переводе чисел из 2-ой в 16-ую  систему счисления надо число разбить на тетрады (по четыре разряда) и записать каждую тетраду эквивалентным двоичным кодом, недостающее число разрядов надо дополнить слева нулями. 

Примеры: 

1. 1001 1110₂ = 9E₁₆

2. 0010 0010₂ = 22₁₆

Алгоритм перевода чисел из 16-ой в 2-ую

Для перевода из 16-ой в 2-ую используется обратное правило.

Каждую цифру шестнадцатеричного числа надо записать четырьмя  разрядами соответствующего ей двоичного кода

Примеры:       

Перевод из 16-ой в 2-ую	17316 = 1011100112
Перевод из 16-ой в 10-ую (используем развернутую форму)	17316 = 1*162 + 7*161 + 3*160 = 256 + 112 + 3 = 37110
Перевод из 10-ой в 16-ую:	37110= А16 ?		37110= 17316

Задания

1. Переведите целые числа из десятичной в шестнадцатеричную систему счисления:

1) 266   2) 1023   3) 1280   4) 2041          Ответы:  1) 10А   2) 3FF   3) 500   4) 7F9

2. Переведите в 2-ую систему счисления числа:    7A₁₆      E4C₁₆         1F₁₆       

3. Переведите в 16-ую систему счисления числа:    01010101₂        11000110₂      11011₂

4. Переведите числа из 10-ой системы счисления в 2-ую и в 8-ую, при этом выполняйте заданную последовательность перевода:

1)   47₁₀   последовательность:    А₁₀ => А₁₆          А₁₀ =>А₂  2)  138₁₀   последовательность:  А₁₀ => А₁₆  =>А₂  3)  128₁₀   последовательность: А₁₀ => А₂  =>А₁₆

5. Переведите заданные числа в указанной последовательности

1) 1368=>А10 => А2 => А16 2)5238=>А2 =>А16 =>А10  3)1001102=>А10 =>А16=> А8 4) 1001102=>А16=>А8 => А10

5) 11110002=>А16=> А8 6) 2B16=>А2 =>А8 7) 1768=>А2 =>А16  8) 3c16=>А2 =>А8

Перевод в какую систему и из какой на ваш взгляд наиболее трудоемкий?

6. Перевести числа :

1)  77₁₀ =А₁₆ ? 2)  72₁₀=А₈ ? 3)  83₁₀  =А₂ ?

WebConnect Ads

Представление о системах счисления.

Система счисления(далее СС) - совокупность приемов и правил для записи чисел цифровыми знаками. Наиболее известна десятичная СС, в которой для записи чисел используются цифры 0,1,:,9. Способов записи чисел цифровыми знаками существует бесчисленное множество. Любая предназначенная для практического применения СС должна обеспечивать:

• возможность представления любого числа в рассматриваемом диапазоне величин;

• единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина);

• простоту оперирования числами;

В зависимости от способов изображения чисел цифрами, системы счисления делятся на непозиционные и позиционные. Непозиционной системой называется такая, в которой количественное значение каждой цифры не зависит от занимаемой ей позиции в изображении числа (римская система счисления). Позиционной системой счисления называется такая, в которой количественное значение каждой цифры зависит от её позиции в числе (арабская система счисления). Количество знаков или символов, используемых для изображения числа, называется основанием системы счисления. Позиционные системы счисления имеют ряд преимуществ перед непозиционными: удобство выполнения арифметических и логических операций, а также представление больших чисел, поэтому в цифровой технике применяются позиционные системы счисления. Запись чисел может быть представлена в виде

,  где A(D) - запись числа A в СС D; D_i - символ системы, образующие базу.

По этому принципу построены непозиционные СС. В общем же случае системы счисления: A(B)=a₁B₁+a₂B₂ +...+a_nB_n. Если положить, что B_i=q*B_i-1, а B₁=1, то получим позиционную СС. При q=10 мы имеем дело с привычной нам десятичной СС. На практике также используют другие СС:

q	Название	Цифры
2	двоичная	0,1
3	троичная	0,1,2
8	восьмеричная	0,...,7
16	шестнадцатиричная	0,...,9,A, ...,F

Каждая СС имеет свои правила арифметики (таблица умножения, сложения). Поэтому, производя какие-либо операции над числами, надо помнить о СС, в которой они представлены. Если основание системы q превышает 10, то цифры, начиная с 10, при записи обозначают прописными буквами латинского: A,B,...,Z. При этом цифре 10 соответствуею знак 'A', цифре 11 - знак 'B' и т.д. В таблице ниже приводятся десятичные числа от 0 до 15 и их эквивалент в различных СС:

q=10	q=2	q=16
0	0	0
1	1	1
2	10	2
3	11	3
4	100	4
5	101	5
6	110	6
7	111	7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F

В позиционной СС число можно представить через его цифры с помощью следующего многочлена относительно q: A=a₁*q⁰+a₂*q¹+...+a_n*qⁿ (1) Выражение (1) формулирует правило для вычисления числа по его цифрам в q-ичной СС. Для уменьшения количества вычислений пользуются т.н. схемой Горнера. Она получается поочередным выносом q за скобки: A=(...((a_n*q+a_n-1)*q+a_n-2)*q+...)*q+a₁ результат вычисления многочлена будет всегда получен в той системе счисления, в которой будут представлены цифры и основание и по правилам которой будут выполнены операции.