6.4. Передаточная функция асинхронного двигателя при управлении по каналу напряжения обмотки статора

_{Рассмотрим динамику работы АД при управлении напряжением на статоре, пренебрегая электромагнитными переходными процесса­ми и учитывая только электромеханические переходные процессы.}

_{Уравнение движения электропривода в операторной форме имеет вид}

,

_{где J - момент инерции привода; М - вращающий момент двигателя;}

_{Mс - момент сопротивления нагрузки.}

_{Вращающий момент двигателя является функцией Ω и UI , а момент сопротивления Мс определяется характером нагрузки и в общем виде может являться функцией скорости вращения}

_{Выведем передаточную функцию в отклонениях, используя при­ем линеаризации статических характеристик.}

_{Разлагая полученное выше уравнение движения ЭП в ряд Тейлора и пренебрегая величинами высшего порядка малости, получим уравнение динамики АД в виде}

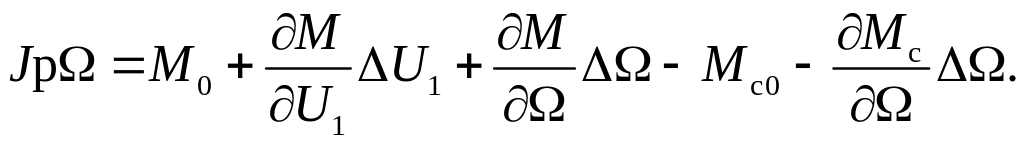
_{Индексом "0" обозначены начальные значения параметров. Вычитая из уравнения динамики уравнение статики М0=Мс 0 , получим}

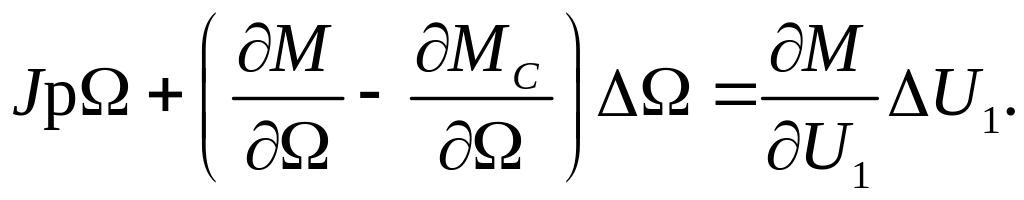
_{или, разделив на выражение в скобках, получим}

,

_{где - электромеханическая постоянная времени;}

_{- коэффициент передачи.}

_{Нетрудно видеть, что при принятых допущениях передаточная функ­ция АД при управлении по каналу напряжения обмотки статора соответствует передаточной функции апериодического звена первого порядка (215):}

₍₂₁₅₎

_{где k и Тм - переменные параметры, зависящие от точки на характеристиках М0= Мc0 , около которой происходит регулиро­вание скорости вращения.}

_{В зависимости от этой точки на механической характеристике M(Ω) и от характера зависимости Mc(Ω) могут изменять­ся не только величина параметров k и Тм, но и вид пере­даточной функции.}

Рис.78. Схема асинхронного электропривода с реверсивным трехфазным ТРН

_{В случае Mc=const и регулирование скорости происхо­дит на участке 0 < s c < sк производная дMc /дΩ=0}, _{а за­висимость вращающего момента двигателя от скольжения может быть принята линейной:}

М=М_Ns_c/s_N.

_{Продифференцируем выражение для момента с учетом того, что скольжения sc}= _(ω1- _Ω)/_{ω1, получим:}

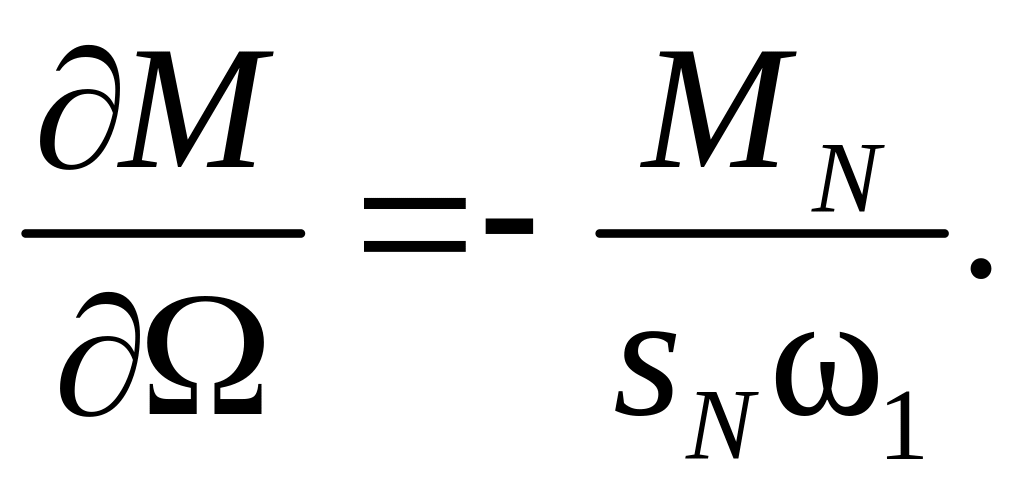
_{Тогда параметры передаточной функции (215) можно определить из соотношений}

₍₂₁₆₎

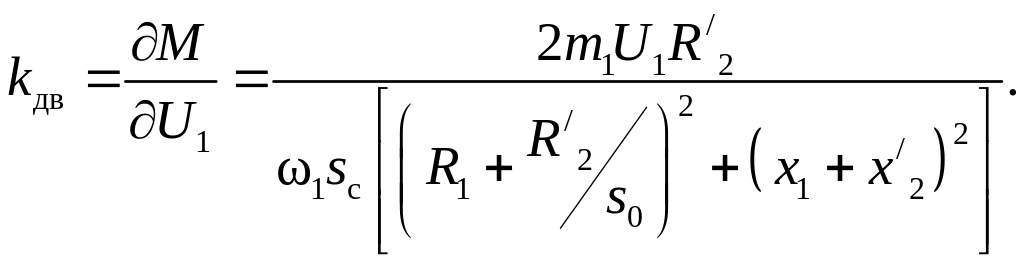(217)

_{Из выражения (217) видно, что kдв зависит от величины скольжения sc и напряжения U1 . Для номинального режима U1 =U1N и sc = sN}

.

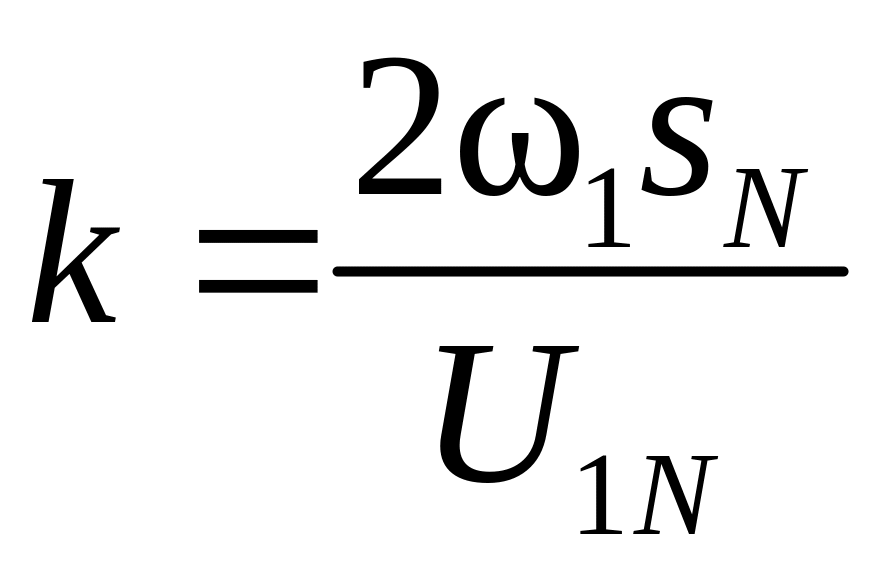6.5. Замкнутая по скорости система асинхронного электропривода с трн

_{Замкнутая по скорости система асинхронного ЭП с ТРН при­ведена на рис.79, а на рис.80 приведены механические характеристики этого привода.}

Управляющие электроды тиристоров подсоединены к выходам СИФУ, которая распределяет управляющие импульсы на все тиристоры и осуще­ствляет их сдвиг в зависимости от входного сигнала управления U_у. К валу двигателя для реализации обратной связи по скорости под­соединен тахогенератор ТГ, ЭДС которого Е_тг сравнивается с за­дающим напряжением скорости U_з.с, снимаемым с задающего потенциометра ЗП. Эти напряжения действуют навстречу друг другу, и их разность образует сигнал управления

U_ур=U_з.с- U_о.сс= U_з.с-k_осΩ, (218)

который поступает на вход СИФУ. При увеличении этого сигнала угол управления тиристорами уменьшается, а подаваемое на дви­гатель напряжение увеличивается, и наоборот. Важно отметить, что при снижении скорости АД в цепи ротора выделяются потери мощ­ности (потери скольжения), которые вызывают его дополнитель­ный нагрев и снижают экономичность работы ЭП.

Рассмотрим работу ЭП при изменении момента нагрузки М_с на валу двигателя и постоянном сигнале задания скорости U_з.с2. Допу­стим, что в исходном положении АД работал с моментом нагрузки М_с1, а затем произошло его увеличение до значения М_с2 В этом случае скорость начнет снижаться и соот­ветственно начнет уменьшаться ЭДС тахогенератора Е_тг, что вы­зовет согласно (215) увеличение напряжения управления U_ур и уменьшение угла управления тиристорами, а значит, приведет к уве­личению подаваемого на АД напряжения. Момент АД будет увели­чиваться, пока не сравняется с моментом нагрузки М_с2. Таким образом, увеличение момента нагрузки приводит к небольшому сни­жению скорости АД, или, другими словами, его характеристики становятся жесткими. При уменьшении момента нагрузки М_с будет автоматически происходить снижение напряжения на АД, т.е. его скорость вращения будет поддерживаться на заданном уровне.

Изменяя значение задающего на­пряжения скорости U_{з. с}, можно получить ряд механических харак­теристик электропривода с относительно высокой жесткостью и не­обходимой перегрузочной способностью АД (см. рис.80).

_{Зависимость напряжения, подаваемого на АД с ТРН, от сигна­ла управления Uуα можно приближенно принять линейной}

, (219)

где

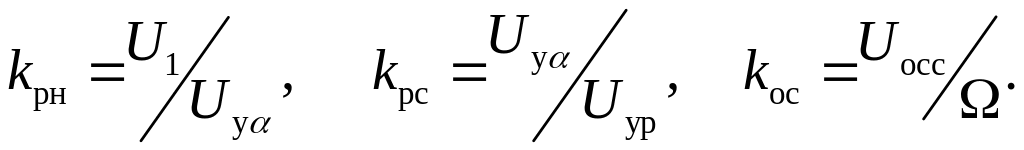
_{Kак показано выше, момент АД пропорционален квадрату напря­жения}

,

где М_е(s_c) - момент при данном скольжении, определяемый по естественной характеристике АД.

При работе с напряжением U_{з. с} =const скорость двигателя в рабочей зоне механической характеристики поддерживается системой регули­рования примерно постоянной, поэтому для режимов малых отклоне­ний от точки статического равновесия зависимость момента от напряжения можно линеаризовать

₍₂₂₀₎

где коэффициент k_м=М_е (s_с), максимальное значение которого можно определить по формуле

Подставив (220) в (219), получим уравнение механической характеристики для рассматриваемого режима

, (221)

где

Таким образом, при принятых допущениях в замкнутой системе формируется линейная механическая характеристика со скоростью идеального холостого хода Ω_{0 зс} и модулем жесткости β_зс. При больших k_ос и k_рс жесткость искусственных механических характеристик получается значительной, и уравнение (221) удовлет­ворительно описывает реальную механическую характеристику. Отли­чие проявляется лишь в режиме, близком к холостому ходу и при значениях, близких к U_1N .

Выражение (221) позволяет рассчитать _{Δ Ω} на заданном диа­пазоне изменения момента нагрузки M_о<M<М_m , если известны значения коэффициентов k_ос, k_м, k_рн, k_рс

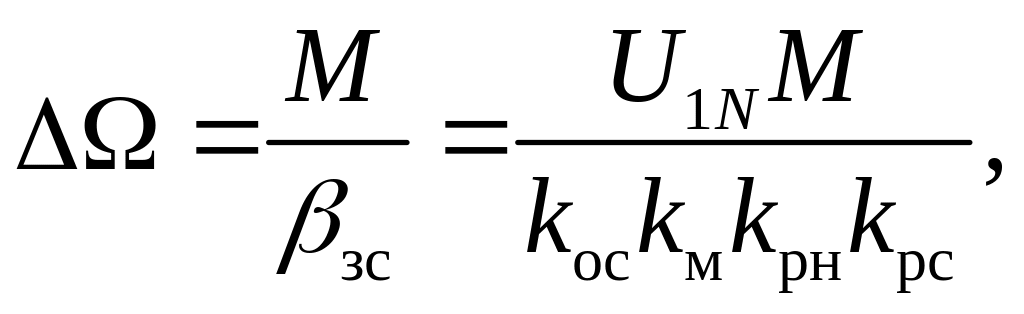₍₂₂₂₎

С другой стороны, если заданы значения момента и величины _{Δ Ω}, можно рассчитать необходимую величину коэффициента усиления ре­гулятора скорости

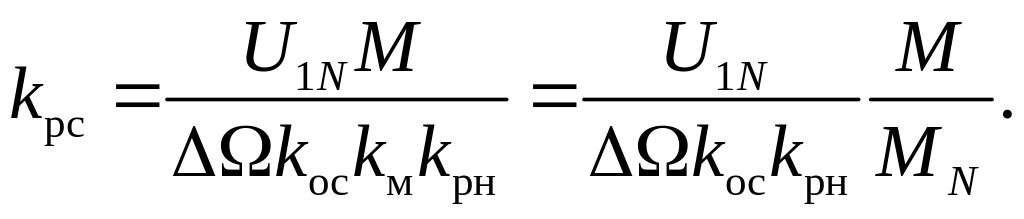
Рис.79.Схема замкнутого по скорости асинхронного ЭП с ТРН

Рис.80.Искусственные механические характеристики замкнутой системы асинхронного ЭП с ТРН.

Вопросы для самоконтроля

1.Дайте пояснения способу регулирования скорости вращения АД путем регулировании величины напряжения, подводимого к обмотке статора.

2. Приведите схемы тиристорного регулятора напряжения и дайте пояснение принципу работы этого регулятора.

3. Приведите выражение и график регулировочной характеристики ТРН.

4. Поясните зависимость коэффициента мощности асинхронного ЭП с ТРН от диапазона регулирования скорости вращения АД.

5.Приведите схему замкнутого по скорости асинхронного ЭП с ТРН, дайте пояснение принципу действия его.

6. Нарисуйте естественную и искусственные механические характеристики асинхронного ЭП с ТРН с обратной связью по скорости.

7. Приведите передаточную функцию асинхронного двигателя при управлении по каналу напряжения обмотки статора.