2.7. Неустановившееся движение при линейных механических характеристиках двигателя и исполнительного органа [1]

При линейных механических характеристиках двигателя и ис­полнительного органа динамический момент ЭП также линейно за­висит от скорости. Такие переходные процессы характерны для ЭП с двигателями постоянного тока независимого возбуждения, а так­же двигателями, характеристики которых могут быть частично или полностью представлены (аппроксимированы) прямыми линиями.

На рис.13, а показаны линейные механические характерис­тики двигателя 1 и исполнительного органа 2, построенные по следующим алгебраическим уравнениям:

М = М_кз - βΩ; (56)

М =М_со + β_сΩ,

где М_кз и М_с0 – моменты двигателя и исполнительного органа при нулевой скорости.

Подставляя эти выражения в уравнение движения (36), получим

М-М_с=М_кз- βΩ - М_со - β_сΩ =J(dΩ/dt). (57)

В обычной для дифференциальных уравнений форме уравнение (57) бу­дет иметь вид

Т_м(dΩ /dt) + Ω = Ω _уст, (58)

где Т_м =J/(β + β_с) – электромеханическая постоянная времени, с;

Ω_уст = (М_кз-М_со)/(β+β_с) – установившаяся скорость, соответству­ющая точке пересечения характеристик двигателя и исполнитель­ного органа.

Выражение (58) по своей форме является линейным неоднород­ным дифференциальным уравнением первого порядка, решение ко­торого Ω (t) имеет вид

(59)

Постоянный коэффициент А определяется из начальных усло­вий переходного процесса: при t = 0 Ω = Ω _нач, т. е. А = Ω _нач - Ω _уст.

Тогда окончательно зависимость изменения скорости от време­ни будет иметь вид

(60)

Запишем момент двигателя в функции времени, исходя из (56):

M(t) = M_кз-βΩ(t). (61)

С учетом того, что

β=ΔМ/ΔΩ =(М_кз - М_уст)/Ω _уст=(М_кз – М_нач) /Ω _нач

после подстановки Ω _нач и Ω _уст получим

(62)

В распространенном для ЭП случае, когда β_с=0 (характерис­тикой исполнительного органа является вертикальная прямая ли­ния), входящие в (60) и (62) параметры будут иметь упрощен­ный вид

Т_м=J/β=JΩ ₀/М_кз;

Ω _уст=(М_кз-М_с)/β.

Время переходного процесса t_{п. п}, за которое скорость двигателя изменится от некоторого начального значения Ω _нач до конечного Ω _кон, определяется в этом случае логарифмированием (60):

t_п.п=T_мln[(Ω _уст- Ω _нач)/(Ω _уст- Ω _кон)]=

=T_мln[(M_уст-M_нач)/(M_уст-M_кон)]. (63)

Анализ полученных выражений (60) и (62) показывает, что скорость и момент двигателя изменяются во времени по экспонен­циальному закону с постоянной времени T_м. На рис. 13, б показа­ны графики переходного процесса разбега: Ω (t) – кривая 3 и М(t)- кривая 4, при увеличении скорости двигателя от Ω _нач до Ω_уст. Отме­тим, что начальные и установившиеся уровни скорости и момента определяются из рис. 13, а, отражая связь установившегося и пере­ходного движений ЭП.

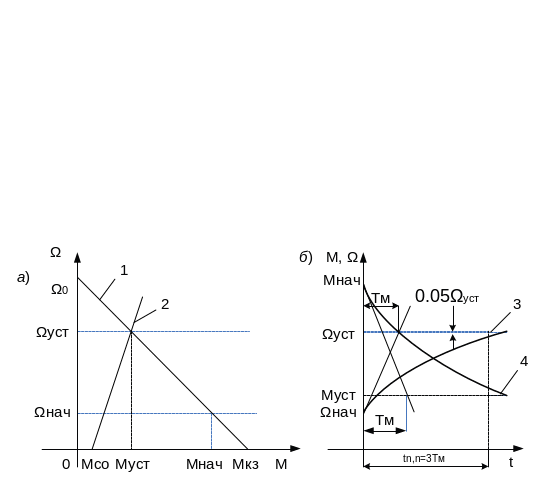
Рис.13. Линейные механические характеристики двигателя и исполнительного органа (а) и график переходного процесса разбега ЭП (б)

Как следует из (63), время достижения установившихся уров­ней скорости и момента (т.е. время переходного процесса) является бесконечно большим. Поэтому в технических расчетах используют так называемое практическое время переходного процесса, прини­маемое обычно равным трем постоянным времени, т.е. t_п.п = 3T_м. За этот интервал времени скорость достигает 95% своего установив­шегося значения.

Постоянная времени Т_м имеет определенное графическое и фи­зическое выражение. На рис. 13, б она равна отрезку, отсекаемому касательной, проведенной к кривой переходного процесса в точке t = 0 на горизонтальной прямой, соответствующей установивше­муся значению переменной (скорости или момента). Количествен­но Т_м равна времени разгона t двигателя без нагрузки (М_с = 0) из неподвижного состояния (Ω_нач = 0) до скорости идеального холос­того хода Ω₀ = Ω_уст под действием пускового момента М_кз. Действи­тельно, из формулы (55) для указанных условий следует, что

t_п.п=t_р=JΩ ₀/М_кз=Т_м.

Задача 12. Выполнить расчет и построение кривых переходного процесса Ω(t) и M(t) при линейной механической характеристике двигателя и следующих исходных данных: Ω_нач = 0; Ω_уст= 150 рад/с, М_нач = М_к.з= 150 Нм; Ω₀= 200 рад/с; М_уст = М_с = 40 Нм; J=0,1 кг·м². Оценить практическое время переходного процесса.

Задача 13. Рассчитать и построить зависимости Ω(t) и M(t) для двигателя, механическая характеристика которого приведена на рис.14, если М_с=0, Ω_нач =200 рад/с.

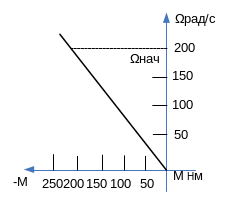
Рис.14. Механическая характеристика к задаче 13

Задача 14. Двигатель, механическая характеристика 3 которого приведе­на на рис.15, работая в установившемся режиме (точка А), преодолевал мо­мент сопротивления М_с1 = 150 Нм. В момент времени t = 0, принимаемый за начало отсчета, произошло скачкообразное изменение момента нагрузки (пря­мые 1, 2) до уровня М_с2 = 250 Нм (точка Б). Рассчитать и построить зависимо­сти Ω(t) и M(t), соответствующие этому увеличению нагрузки.

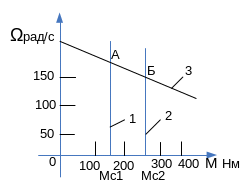
Рис.15. Механические характеристики к задаче 13

Вопросы для самоконтроля

1. Напишите полные уравнения движения для вращательного и поступательного характера движения. 2. Преобразуйте полные уравнения движения в упрощенные, обоснуйте возможность этого преобразования.

3. Приведите уравнения двухмассовой системы ЭП, дайте пояснения параметрам этого уравнения.

4. Нарисуйте механические характеристики двигателей постоянного тока с независимым и последовательным возбуждением, асинхронного двигателя и синхронного двигателя.

5. Нарисуйте механические характеристики исполнительных органов рабочих машин, соответствующие работе с постоянным моментом (с характером нагрузки типа «сухое трение»), с постоянной мощностью, с вентиляторным характером нагрузки и с характером нагрузки типа «вязкое трение».

6. Как оценить жесткость механических характеристик двигателя и исполнительного органа рабочей машины.

7. Напишите формулу проверки устойчивости работы ЭП.

8. Нарисуйте график переходного процесса разбега ЭП при постоянном и положительном значении динамического момента.

9. Дайте определение понятию «практическое время переходного процесса».

10. Нарисуйте график переходного процесса разбега ЭП при линейных механических характеристиках двигателя и исполнительного органа. Поясните методику определения электромеханической постоянной времени ЭП по характеристикам, приведенным на этом графике.