2.6. Неустановившееся движение электропривода при постоянном динамическом моменте

Неустановившееся движение ЭП имеет место, когда моменты дви­гателя и нагрузки отличаются друг от друга, т. е. М≠М_с. В этом слу­чае динамический момент М_дин не равен нулю и происходит увеличе­ние или снижение скорости движения. Наиболее типичными приме­рами неустановившегося движения в ЭП являются пуск, торможение и реверс двигателя, его переходы с одной скорости на другую в про­цессе ее регулирования или изменения нагрузки на валу.

Неустановившееся движение возникает при переходе ЭП из ус­тановившегося движения с одними параметрами к установившему­ся движению с другими параметрами (если, конечно, движение ус­тойчивое). По этой причине неустановившееся движение называют также переходным процессом или переходным режимом ЭП.

Целью рассмотрения неустановившегося движения является по­лучение зависимостей механических переменных (координат) ЭП – моментов, скорости и угла поворота вала двигателя от времени. Рассмотрим переходные процессы в механической части ЭП, обус­ловленные инерционностью движущихся элементов. Иногда такие процессы называют механическими [1].

Искомые зависимости получим решением (интегрированием) дифференциального уравнения механического движения (45), а также дифференциального уравнения Ω = dφ/dt, связывающего угол поворота φ вала двигателя и его скорость Ω.

Для решения этих уравнений необходимо знать законы изменения моментов двигателя и нагрузки, а также массы и моменты инерции движущихся элементов и начальные (нулевые) значения переменных.

В общем случае моменты двигателя и нагрузки, а иногда и мо­мент инерции могут являться функциями времени, скорости и по­ложения ИО (угла поворота вала двигателя).

Из всего многообразия возможных переходных процессов рас­смотрим наиболее часто имеющие место случаи, когда моменты двигателя и нагрузки ЭП являются постоянными величинами, не зависящими от скорости или времени, а моменты инерции и массы движущихся элементов не изменяются в переходных процессах. Другие возможные переходные процессы см. в [1 ].

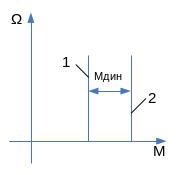
Рис.11. Механические характеристики двигателя (2) и исполнительного органа (1)

На рис. 11 приведены механические характеристики двигате­ля 2 и нагрузки (исполнительного органа) 7, при которых их мо­менты неизменны, т.е. динамический момент постоянен и положи­телен. Уравнение движения (46) в этом случае решается методом разделения переменных и ее решение имеет вид

Постоянная интегрирования С находится из начального условия переходного процесса: при t =0 Ω = Ω _нач. Подставляя это условие в (53), получим С = Ω _нач. Тогда окончательно (53) принимает вид

Полученная формула показывает, что при разбеге ЭП (см. рис. 11) скорость Ω линейно зависит от времени. При (М - М_с) > 0 скорость увеличивается (прямая 4), а при (М - М_с) < 0 – снижается. Мо­мент двигателя от времени не зависит, поэтому зависимость М(t) изображается прямой линией 3.

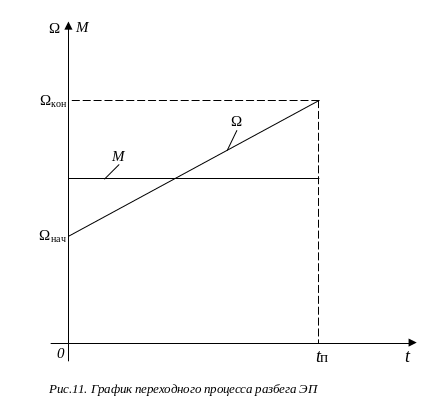
Рис.12. График переходного процесса разбега ЭП: М - динамический момент, Ω -угловая скорость вращения

Время переходного процесса t_п.п, за которое скорость изменится от некоторого начального Ω _нач до конечного Ω_кон уровня, определя­ется из (54) при подстановке в нее t = t_{п. п} и Ω = Ω _кон:

t_{п. п}=J(Ω _кон- Ω _нач)/(М - М_с). (55)

Задача 9. Рассчитать и построить зависимость Ω(t) при следующих исход­ных данных: М= 50 Нм; М_c= 100 Нм; J= 0,1 кг•м²; Ω_нач= 100 рад/с. Рассчитать время переходного процесса, за которое скорость снизится в два раза.

Задача 10. Определить динамический момент, который при J=0,2 кг·м² обеспечит увеличение скорости на 200 рад/с за время t_{п. п}= 1 с.

Задача 11. Получить общее выражение для определения зависимости угла поворота вала двигателя от времени φ(t) для случая постоянного динамическо­го момента и оценить вид этой зависимости.