6.1. Электрическая цепь с активным сопротивлением
Электрический ток проводимости в металлах представляет собой направленное движение свободных электронов, скорость и направление которого определяются значением и полярностью приложенного к проводнику напряжения. При движении электроны сталкиваются с атомами проводящего вещества и кинетическая энергия электронов, запасенная ими при ускорении, превращается в тепловую энергию, затрачиваемую на нагрев проводника и рассеиваемую в окружающую среду. Это необратимый активный процесс преобразования электрической энергии, который количественно определяется сопротивлением R. Потому его называют активным сопротивлением.
Активным сопротивлением обладают практически все материалы, проводящие электрический ток (металлы, уголь, электролиты). Таким образом, все провода, обмотки, реостаты и другие элементы цепи обладают активным сопротивлением. Элементы электрической цепи, обладающие только активным сопротивлением R, называют резисторами.
При рассмотрении электрических цепей постоянного тока сопротивление R называли просто сопротивлением. В теории цепей синусоидального тока его называют активным сопротивлением. С одной стороны, это вызвано тем, что необходимо привести название этого сопротивления в соответетвие с названиями других по характеру сопротивлений (индуктивное, емкостное, реактивное, полное), характеризующих цепь синусоидального тока, с другой тем, что один и тот же проводник оказывает большее сопротивление движению электронов при синусоидальном токе, чем при постоянном (это будет показано далее), т. е. активное сопротивление больше сопротивления постоянному току.
Пусть к зажимам цепи с активным сопротивлением R (рис. 6.1, а) приложено напряжение источника питания u Um sin t.
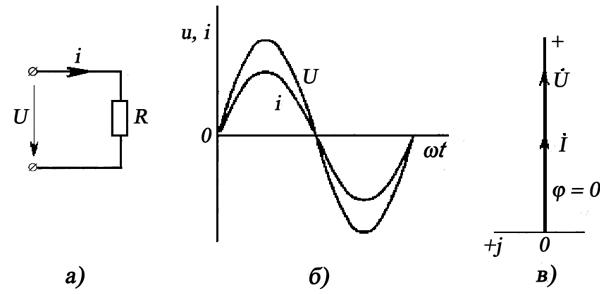
Рис. 6.1. Электрическая цепь с активным сопротивлением R. a схема; б изменение мгновенных значений тока и напряжения; в векторная диаграмма.
Для простоты принимается, что начальная фаза напряжения равна нулю, так как для установившегося режима начальная фаза не имеет никакого значения.
В соответствии со вторым законом Кирхгофа для мгновенных значений напряжения имеем u R i. Решая, это уравнение относительно тока i и заменяя u на Um sin t, получаем
i (Um/R) sin t Im sin t, (6.1)
причем амплитуда тока в цепи
Im Um/ R. (6.2)
Из уравнения (6.1) видно, что ток в элементе с активным сопротивлением совпадает по фазе с напряжением на этом элементе (рис. 6.1, б).
Так как действующие значения напряжения и тока в раз меньше их максимальных значений, то аналогично (6.2) можно записать I U/R, т. е. действующие значения синусоидальных напряжений и тока связаны между собой законом Ома так же, как постоянные напряжение и ток.
На векторной диаграмме (рис. 6.1, в) комплексные значения напряжения U и тока I в цепи представлены векторами на комплексной плоскости. Начала векторов совмещены с началом координат, длины векторов в соответствующем масштабе равны действующим значениям напряжения и тока. Вещественная ось направлена вертикально, а мнимая горизонтально. Начальный вектор совмещаем с положительным направлением вещественной оси. Для цепи с активным сопротивлением векторы напряжения и тока совпадают по направлению.
Рекомендация:
Для самоконтроля полученных знаний выполните тренировочные задания из набора объектов к текущему параграфу