Аксиомы метрики

Все перечисленные выше расстояния, обладают некими универсальными свойствами:

1. ρ(Х,У)≥0, то есть расстояние неотрицательно.

2. Если Х=У, то ρ(Х,У)=0.

3. ρ(Х,У)=ρ(У,X) – свойство симметрии.

4. ρ(Х,Z)+ρ(Z,У)≥ρ(Х,У) – неравенство треугольника.

При выполнении всех этих аксиом, расстояние между точками называется метрикой, а пространство – метрическим пространством с метрикой ρ.

Рассмотрим на примере. Пусть есть карта местности и две речки, обозначенные кривыми Г и Г (рис. 3.4). Нам надо построить канал т. е. отрезок, чтоб было как можно меньше затраты ресурсов.

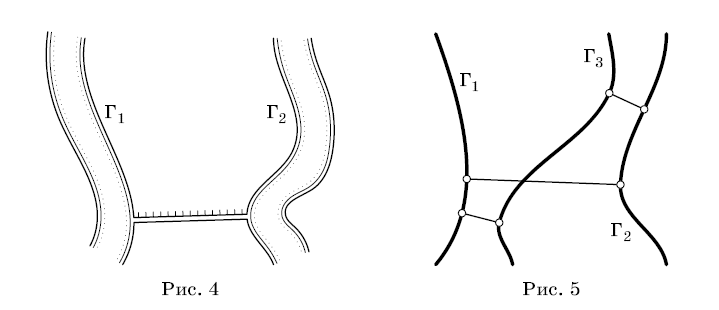
Рис 3.4 Рис 3.5

Тогда естественно ввести такое расстояние:

Г ,Г

Г

Г

Как видно, это разумно определенное расстояние, но оно не удовлетворяет 4 аксиоме метрике. Действительно, для трех речек (рис.3.5) оказывается

Г ,Г Г ,Г Г ,Г

Это пример расстояния, которое нельзя назвать метрикой. Поэтому пространство кривых с таким расстоянием нельзя назвать метрическим.

Отметим также, что элементами метрических пространств могут быть не только точки, но и кривые, множества, функции. Главное – чтобы можно было определить расстояние между ними.

Зоны Дирихле в метрических пространствах и их приложения

Рассматривать обычное евклидово расстояние на плоскости:

( ) .

В этом случае зоны Дирихле нетрудно построить для любого числа точек. Так как серединный перпендикуляр является геометрическим местом точек равноудалённых от двух данных, то двух точек достаточно соединить их отрезком и провести серединный перпендикуляр. Эта прямая и будет делить пространство на зоны Дирихле (рис. 3.6).

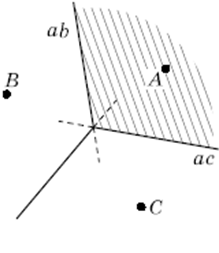
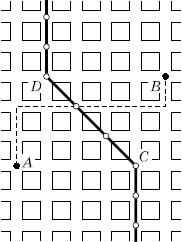
Рис 3.6 Рис 3.7

Зоны Дирихле возникают во многих прикладных задачах. Например, пусть необходимо разделить город на зоны Дирихле относительно станций метро. Воспользуемся метрикой ( ). Представим сетку улиц с правильной планировкой и две станции метро А и В (рис 3.7).

Здесь разделителем плоскости на сферы влияния будет множество точек, от которых до станции А и В будет одинаковое расстояние. В это множество попадают точки отрезка CD, которые являются серединами кратчайшего пути от станции метро А до станции метро В (один из них показан пунктиром на рис. 3.7). Далее при перемещении вдоль линии-разделителя ниже точки С или выше D путь увеличивается на 1 квартал.

Зоны Дирихле также используются в теории кодирования. Пусть, например, нужно автоматически исправлять ошибки при передаче закодированных сообщений. Рассмотрим слова, записанные в двоичной системе счисления (0,1) и состоящие из 5 букв. За расстояние примем количество побуквенных различий в словах. Например, расстояние от 01011 и 11101 равно 3. В реальности используются более длинные слова. В качестве центров притяжения используются только осмысленные слова.

Так, если произошел сбой в передаче, то некоторые слова изменились на близкие к ним. А так как всё пространство делено на Зоны Дирихле относительно осмысленных слов, то мы можем изменить сообщение, заменяя слова с ошибками на ближайшие к ним. Именно так работают некоторые механизмы автоматического исправления в теории кодирования [1].