Приложения
1 . Рисунки к основной части работы
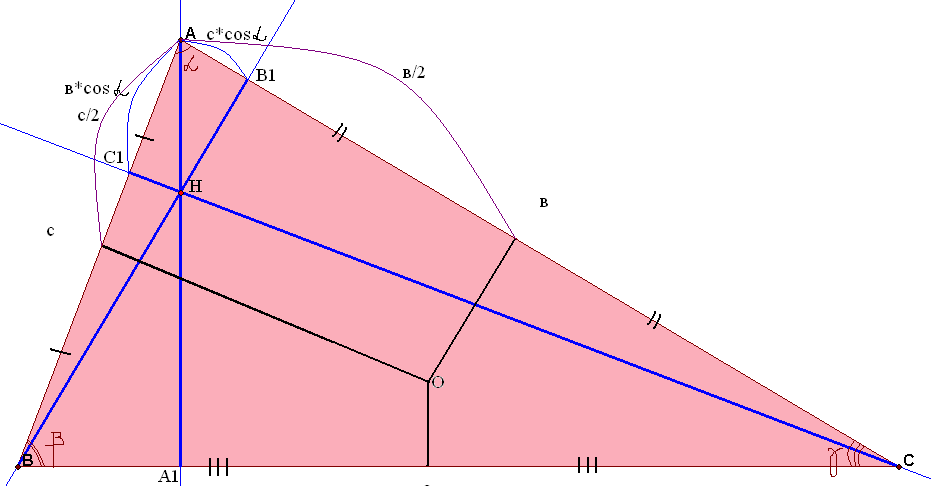Рис.
1.1 Рис.
1.2
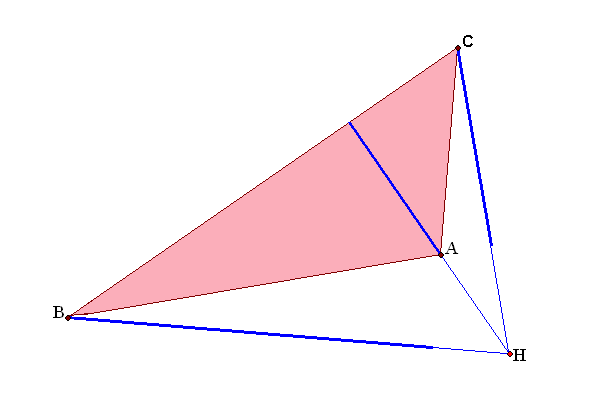Рис.
1.3
Рис. 1.4
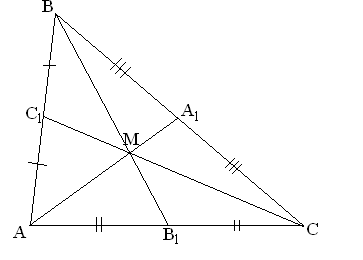
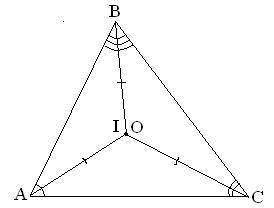
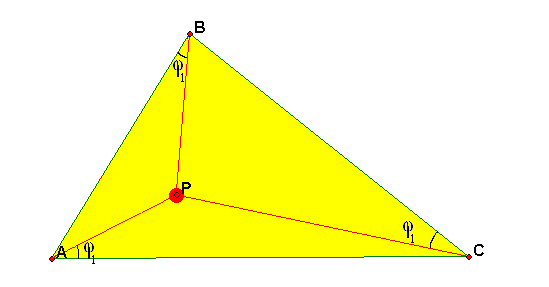
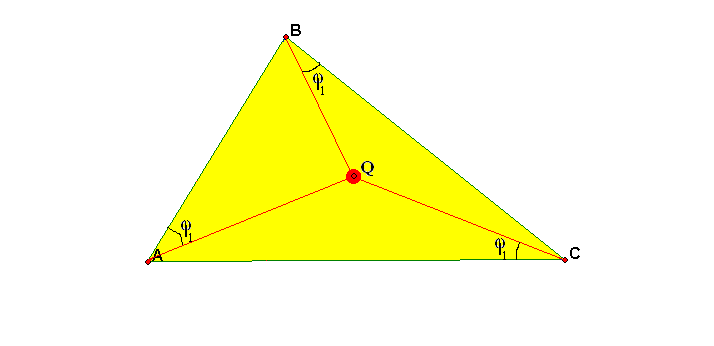
Рис. 1.6
Рис. 1.5
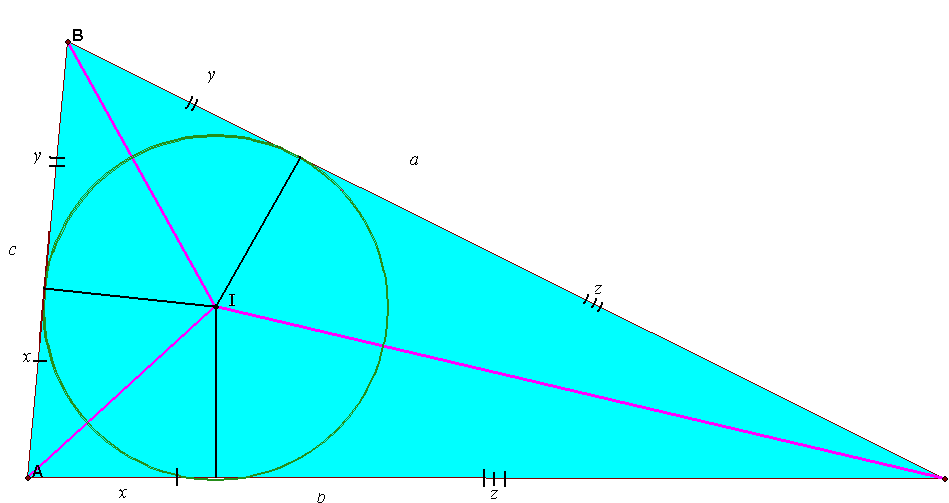
Рис. 1.7
Рис. 1.8 Рис.1.9
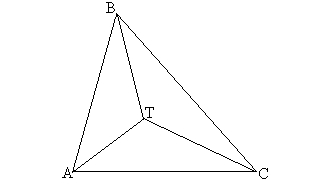
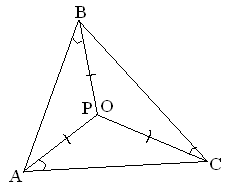
Рис. 1.10 Рис. 1.11
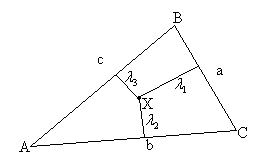
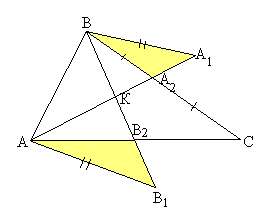
Рис.
2.1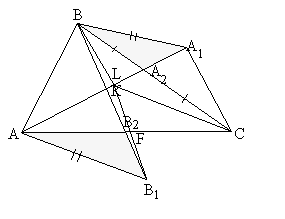 
Рис. 2.2
Рис. 2.3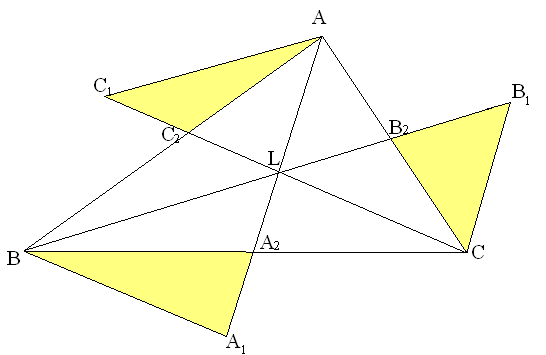
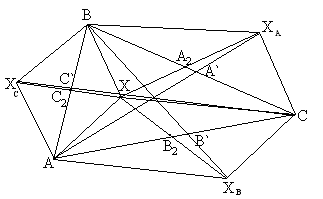
Рис. 2.4 Рис. 2.5
2. Метрические пространства и зоны Дирихле Какие бывают расстояния
Наверное, каждый знает, что такое значит «расстояние между двумя местами», но даже в повседневной жизни мы вкладываем в него разные значения в зависимости от ситуации. Если для лётчика это расстояние будет измеряться вдоль прямой, то автомобилист будет считать расстояние вдоль шоссейных дорог, которые могут существенно отклоняться от прямолинейного пути.
На плоскости
расстояние между двумя точками
и
на плоскости мы
определяем так: соединяем эти точки
отрезком и берём его длину за расстояние
между этими точками. Расстояние можно
вычислить по формуле
(
)
(«Евклидово
расстояние»).
Но легко привести примеры, в которых более естественным оказывается другое определение. Допустим мы находимся в городе с «очень правильной» планировкой. В этом городе k*n прямоугольных кварталов, разделенных n-1 «горизонтальными» и k-1 вертикальными улицами (Рис. 3.1).
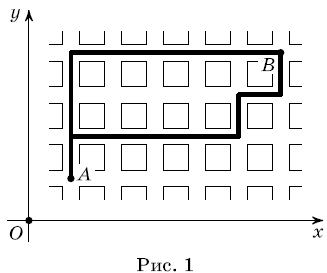
Рис 3.1
В таком городе нет смысла пользоваться обычным расстоянием, если нас интересует расстояние от перекрёстка до на плоскости будет определяться формулой: .
Также существует
метрика
(
(
)).
Этому расстоянию можно придать такой
физический смысл. Пусть мы должны
поддерживать определённую температуру
в двух комнатах и измеряем показатели
двумя термометрами. Пусть в первой
комнате нужно поддерживать температуру
,
а во второй -
.
Показания термометров -
и
соответственно. Нужно следить за тем,
чтобы температура не отклонялась от
нормы. Тогда определённое так расстояние
между показаниями термометров показывает,
на сколько градусов произошло отклонение
от нормы
Аналогичные
расстояния можно ввести и между точками
и
трехмерного
пространства.
Шары
Если на множестве определено расстояние, то с его помощью можно описать геометрические объекты все точки которого лежат в пределах этого расстояния.
Единичный шар –
это множество точек, которые удалены
от центра на расстояние не более, чем
1. Вот запись этого множества:
.
На рис 3.2 мы видим представление единичного шара для различных расстояний.
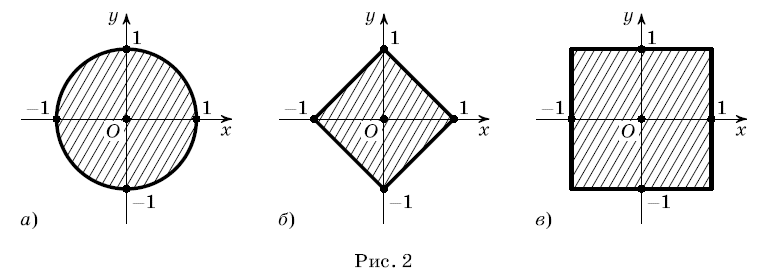
Рис 3.2
Для евклидова
расстояния единичный шар будет выглядеть
так, как показано на рисунке 3.2(а). А рис.
3.2(б) является представлением расстояния,
названым
.
Рис 3.2(в) – представление метрики (это
будет квадрат со сторонами параллельными
осям).
Можно получить бесконечное количество способов задания расстояния если в формуле, определяющей евклидово расстояние, заменить 2 на ρ, ρ≥1. Получим такое расстояние : ( ) .
Если ρ постепенно
увеличивается от 1 до 2, то шар будет
раздуваться от ромба до круга (Рис. 3.3).
А дальше, когда ρ станет больше 2, то шар
будет всё больше заполнять большой
квадрат. Т. е. при
получается квадрат, который является
единичным шаром для расстояния
.
Поэтому, расстояние, названое
,
можно обозначить, как
(как при ρ, стремящимся к ∞ ).
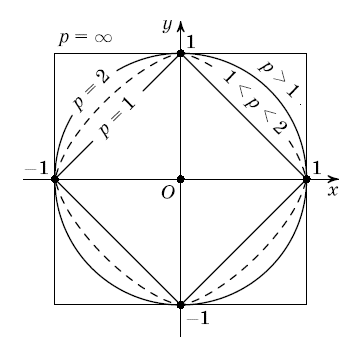
Рис 3.3