
- •Зоны дирихле вершин треугольника
- •Содержание
- •Раздел 1 6
- •Раздел 2 16
- •Список условных обозначений
- •Введение
- •Раздел 1 о принадлежности некоторых замечательных точек треугольника зонам дирихле его вершин
- •Центр описанной окружности
- •Ортоцентр
- •1.2.1. При каких условиях ортоцентр
- •1.2.2. При каких условиях ортоцентр принадлежит
- •1.2.2.1. Для остроугольного треугольника:
- •1.2.2.2. Для прямоугольного треугольника:
- •1.2.2.3. Для тупоугольного треугольника:
- •Центроид
- •1.3.1. При каких условиях центроид находится на пересечении зон Дирихле всех вершин треугольника?
- •1.3.2. При каких условиях центроид
- •Инцентр
- •1.4.1. При каких условиях инцентр
- •1.4.2. При каких условиях инцентр
- •Точки Брокара
- •1.5.1. При каких условиях первая (вторая) точка Брокара
- •1.5.2. При каких условиях первая точка Брокара
- •1.5.3. При каких условиях вторая точка Брокара
- •Точка Торричелли
- •1.6.1. При каких условиях точка Торричелли
- •1.6.2.При каких условиях точка Торричелли
- •Теорема о принадлежности замечательных точек треугольника зонам Дирихле его вершин
- •Раздел 2 задачи
- •2.1. Задача 1.
- •2.2. Задача 2.
- •2.3. Задача 3.
- •2.4. Задача 4.
- •2.5. Задача 5.
- •Список использованных источников
- •Приложения
- •1 . Рисунки к основной части работы
- •2. Метрические пространства и зоны Дирихле Какие бывают расстояния
- •Аксиомы метрики
- •Зоны Дирихле в метрических пространствах и их приложения
- •3. Интересный факт
- •4. Компьютерное приложение к работе
Раздел 2 задачи
В этом разделе рассмотрены пять авторских задач, в которых используется полученная теорема.
2.1. Задача 1.
Предприниматель
купил 3 торговых зоны (А, В, С) в сельской
зоне. Ему нужно выбрать место для склада
Х, до которого нужно отремонтировать
дороги. Где выбрать Х так, чтобы
минимизировать затраты на ремонт дорог
и перевозку товаров. Считаем, что затраты
на ремонт пропорциональны
![]() +
+![]() +
+![]() ,
а затраты на перевозку пропорциональны
,
а затраты на перевозку пропорциональны
![]() +
+![]() +
+![]() (
(![]() — площади торговых зон).
— площади торговых зон).
Для решения задач
я буду использовать хорошо известный
принцип упорядоченных наборов для трёх
чисел: если
![]() ,
,
![]() ,
то
,
то
![]() ,
где
,
где
![]() —
некоторая перестановка
—
некоторая перестановка
![]() .
Его доказательство представлено в [6,
стр. 14].
.
Его доказательство представлено в [6,
стр. 14].
Решение
Возможны такие случаи:
Все углы АВС меньше 120˚.
Треугольник АВС имеет больший угол равный или больший 120˚.
Точки А, В, С лежат на одной прямой.
Для первого случая ответом является точка Торричелли. По её свойству:
![]() ,
значит
,
значит
![]() .
.
Для второго случая ответом будет точка Ферма, которая будет совпадать с вершиной тупого угла.
Если точки А, В, С
образуют прямую, то
![]() совпадает с точкой, лежащей между двумя
другими.
совпадает с точкой, лежащей между двумя
другими.
Пусть
![]() и
и
![]() .
По доказанному неравенству:
.
По доказанному неравенству:
![]()
![]() .
.
В отличие от
стандартной задачи Ферма – Торричелли
– Штейнера здесь введены коэффициенты
при длинах расстояний и способ решения
этой задачи. Используя теорему о
принадлежности точки Торричелли зонам
Дирихле вершин треугольника и зная
длины
![]() ,
,
![]() ,
,
![]() можно упорядочить расстояния
можно упорядочить расстояния![]() ,
,
![]() ,
,
![]() наибольшее и наименьшее.
наибольшее и наименьшее.
2.2. Задача 2.
Предприниматель
купил 3 торговых зоны (А, В, С) в деревенской
зоне. Где нужно выбрать место для склада
Х, до которого нужно отремонтировать
дороги так, чтобы минимизировать затраты
на ремонт дорог и перевозку. Затраты на
ремонт пропорциональны
![]() +
+![]() +
+![]() ;
а затраты на перевозку пропорциональны
;
а затраты на перевозку пропорциональны
![]() +
+![]() +
+![]() ,где (
— площади магазинов).
,где (
— площади магазинов).
Решение
По теореме Лейбница
[7, стр. 69] для
![]() :
:
![]() ,
значит искомая точка – центроид.
,
значит искомая точка – центроид.
![]()
Решение второй
части задачи (![]() )
аналогично решению второй части задачи
№1.
)
аналогично решению второй части задачи
№1.
2.3. Задача 3.
Даны 3 точки
плоскости (А, В, С), образующие треугольник
АВС, известны длины его сторон. Найти
точку Х внутри треугольника такую, что
![]() (рис 2.1). Пусть даны
(рис 2.1). Пусть даны
![]() — некоторые положительные числа. Каким
образом нужно расставить коэффициенты
таким образом, чтобы минимизировать
величину
— некоторые положительные числа. Каким
образом нужно расставить коэффициенты
таким образом, чтобы минимизировать
величину
![]() ,
где
,
где
![]() — некоторые перестановки
— некоторые перестановки
![]() .
.
Решение
Умножим
 на
на
 .
Имеем:
.
Имеем:
![]() =
=![]()
![]()
По неравенству
Коши (неравенство о среднем арифметическом
и среднем геометрическом):
![]() ,
,
![]() ,
,
![]() ,
значит:
,
значит:
![]()
![]()
Равенство достигается при
![]() ,
,
![]() ,
,
![]() или
или
![]() ,
т. е. Х=I (инцентр).
,
т. е. Х=I (инцентр).
Если даны коэффициенты
![]() ,
то решение задачи
,
то решение задачи
![]() аналогично решению второй части задачи
№1.
аналогично решению второй части задачи
№1.
2.4. Задача 4.
Дано:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (рис 2.2).
(рис 2.2).
Доказать: а)
Точка К – центроид
,
б)
![]() .
.
Доказательство
Проведём
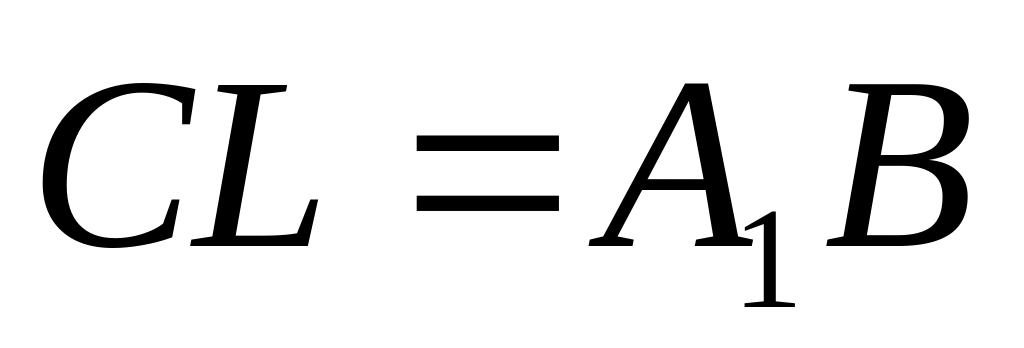 ,
,
 (см рис. 2.3.).
(см рис. 2.3.). - параллелограмм
(Так как
- параллелограмм
(Так как
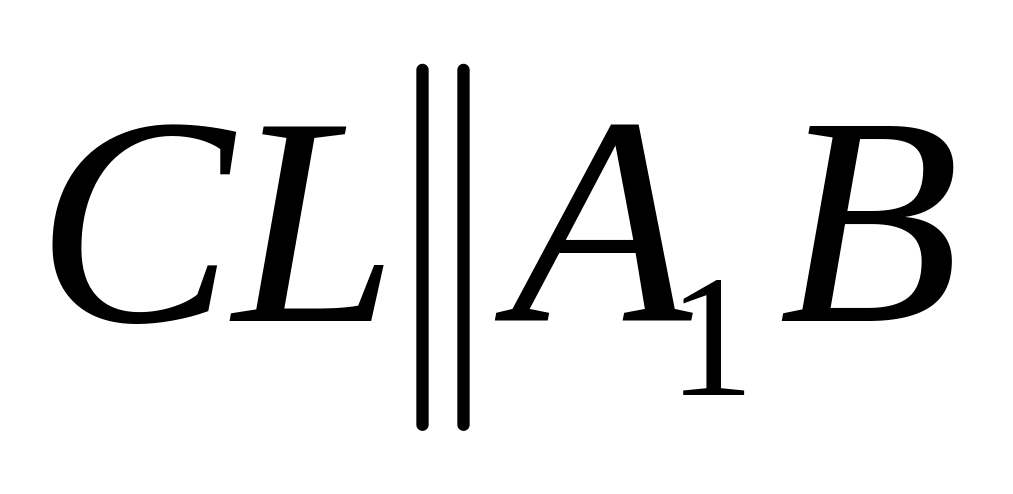 и
).
и
).Так как
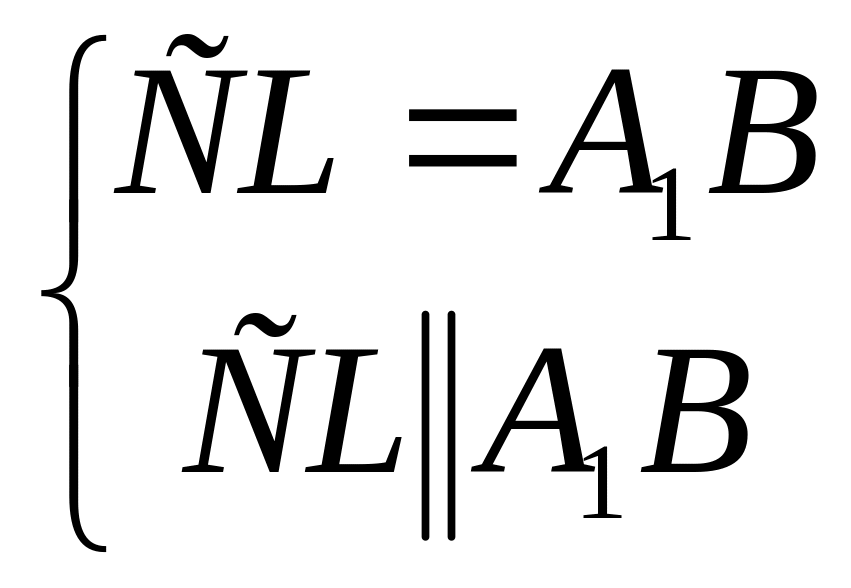 и
и
 ,
то
,
то
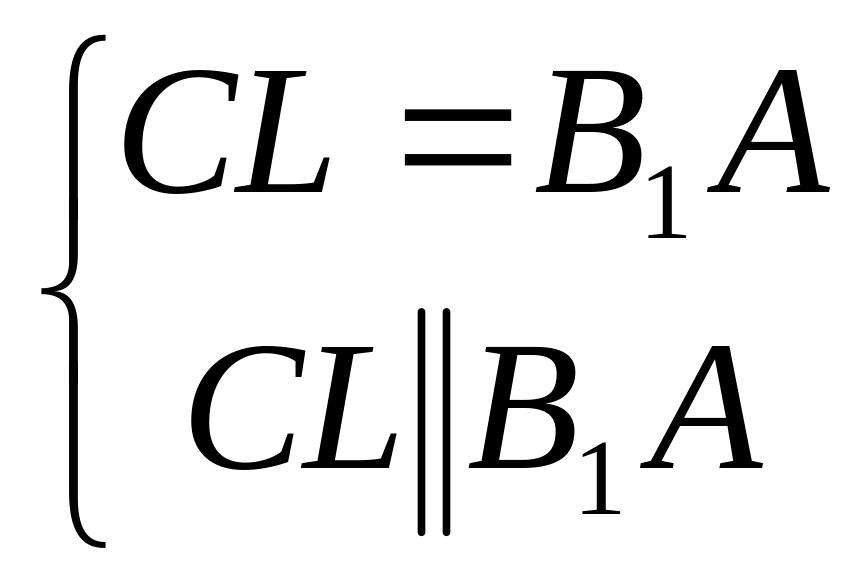 ,
значит
,
значит
![]() —
параллелограмм.
—
параллелограмм.
Так как , то и
 -
диагонали
,
значит
-
диагонали
,
значит
 .
.
![]() .
.
Так как
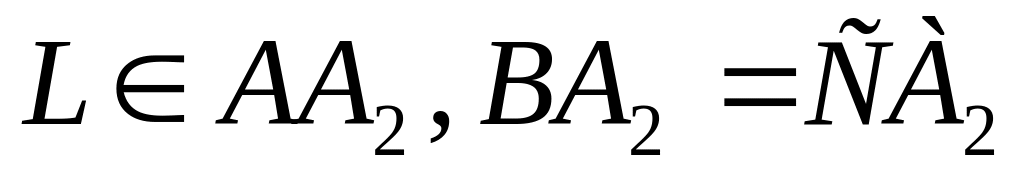 и
и
 ,
то L – центроид
,
значит
,
то L – центроид
,
значит
![]()
В параллелограмме :
![]() .
.
Так как
![]() (по
условию) и
(по
условию) и
![]() (по
доказанному), то
(по
доказанному), то
![]() и L – центроид
,
то
и L – центроид
,
то
![]() – центроид
.
– центроид
.
Так как
![]() и
и
![]() параллелограммы, то
параллелограммы, то
![]() .
.
Так как
![]() ,
то по теореме о принадлежности центроида
зонам Дирихле вершин имеем (см. с. 16):
,
то по теореме о принадлежности центроида
зонам Дирихле вершин имеем (см. с. 16):
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
