1.5.1. При каких условиях первая (вторая) точка Брокара
находится на пересечении зон Дирихле всех вершин треугольника?
Это возможно только
в том случае, если точка Р (Q) совпадает
с центром описанной окружности. Пусть
это так (рис. 1.10). Имеем
,
так как
— центр описанной окружности
,
,
— равнобедренные
,
,
(как углы при основании равнобедренных
треугольников). Так как
– первая точка Брокара, то
,
то есть
(
— равносторонний). Аналогично, вторая
точка Брокара (Q) совпадает с центром
описанной окружности только в правильном
треугольнике.
1.5.2. При каких условиях первая точка Брокара
принадлежит зоне Дирихле вершины А?
Задание: найти условия на элементы треугольника, при которых верно:
.
А) Из
имеем:
,
,
или
,
то есть
.
Б) Из
имеем:
,
,
или
,
то есть
.
В) Из
имеем:
,
,
или
,
то есть
.
По теореме синусов
(для
,
,
):
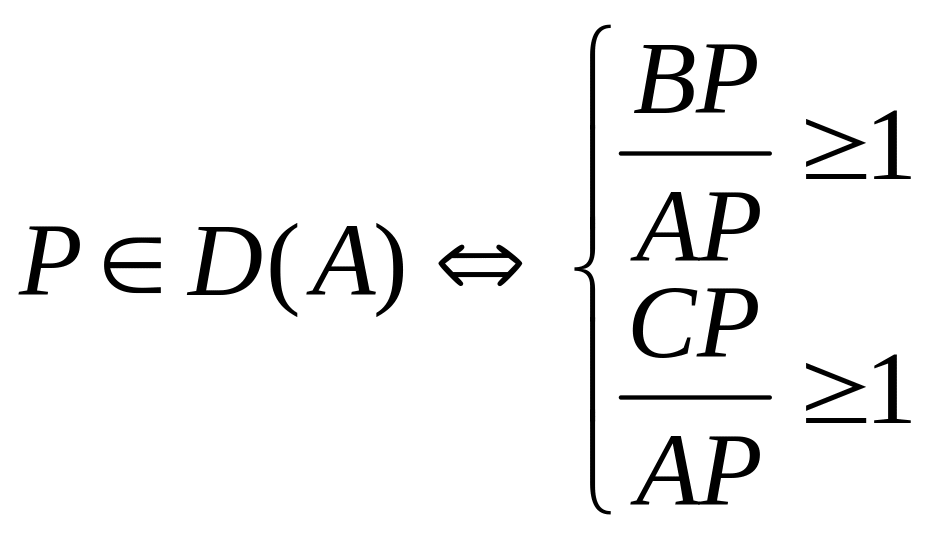
Решим предыдущую систему. Начнём с первого неравенства.
.
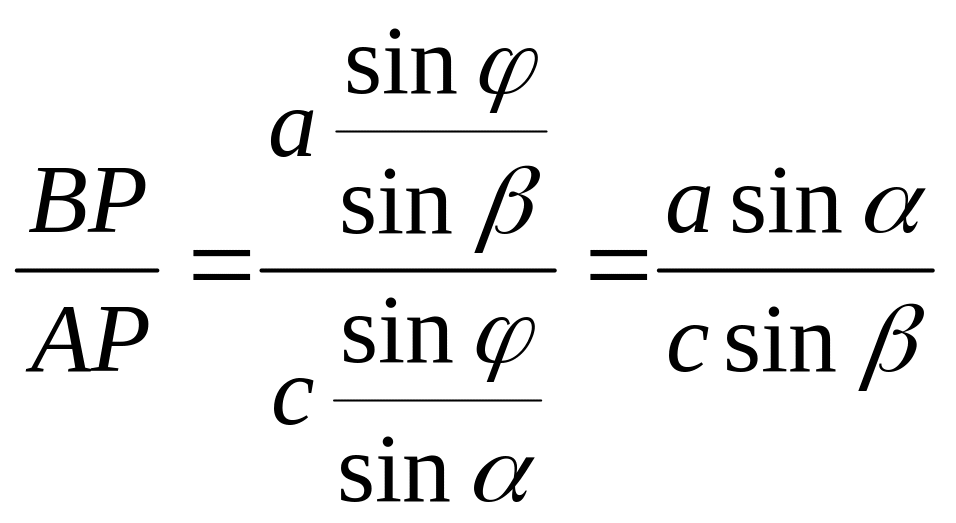По теореме синусов:
,
.
Значит,
.
Рассмотрим второе
неравенство.
.
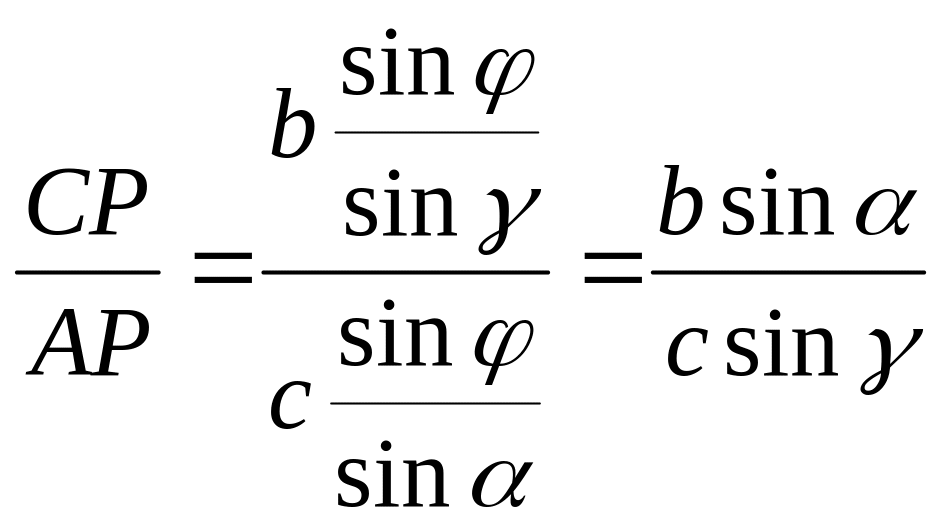По теореме синусов:
,
Значит,
.
Система
верна при
Вывод:
.
1.5.3. При каких условиях вторая точка Брокара
принадлежит зоне Дирихле точки А?
Задание: найти условия элементов треугольника, при которых верно:
.
А) Из
имеем:
,
,
или
,
то есть
.
Б) Из
имеем:
,
,
или
,
то есть
.
В) Из
имеем:
,
,
или
,
то есть
.
По теореме синусов:
.
.
.
.
Решим предыдущую систему. Начнём с первого неравенства.
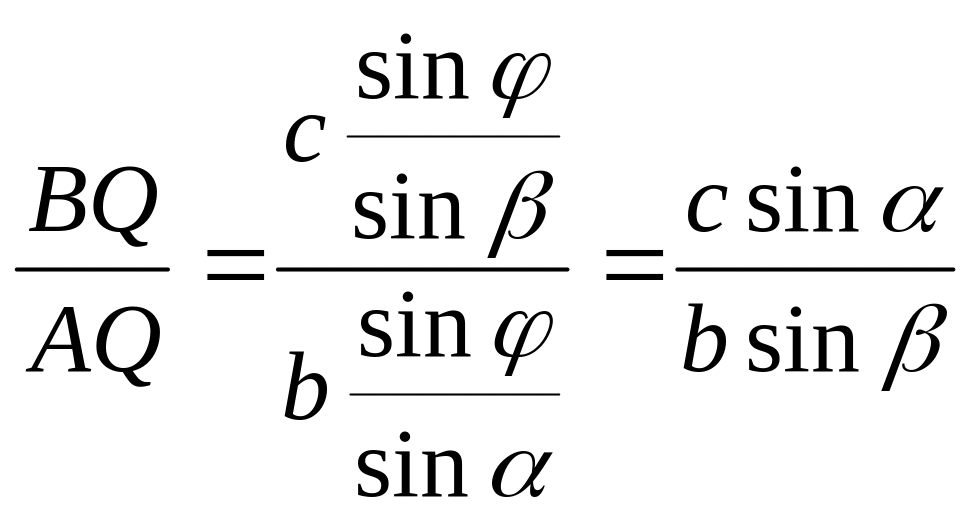
По теореме синусов:
,
.
Значит,
.
Рассмотрим второе
неравенство.
.
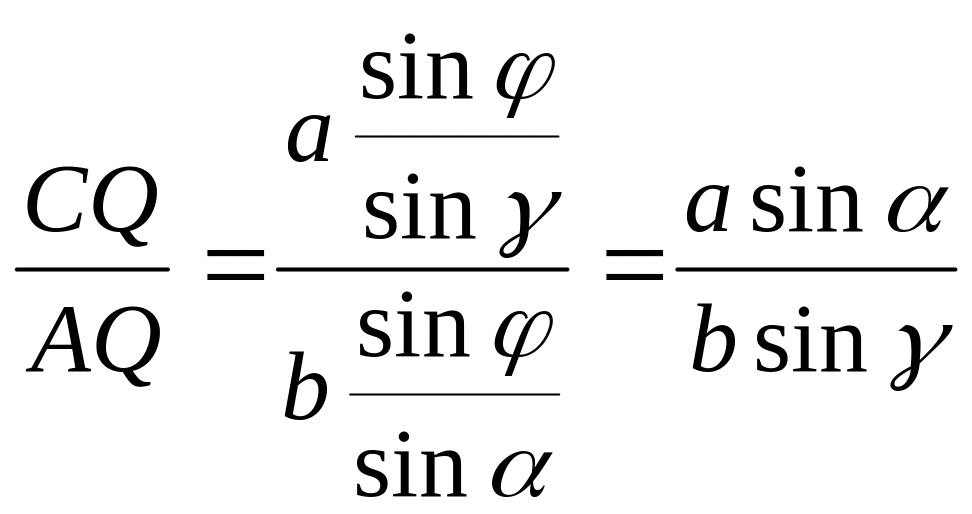По теореме синусов:
,
.
Значит,
Система
верна при
Вывод:
.
При каких условиях обе точки Брокара
принадлежат зоне Дирихле вершины А?
.
Точка Торричелли
Точка Торричелли — точка треугольника (рис. 1.11), из которой все стороны видны под углом в 120°. Существует только в треугольниках с углами меньшими 120° [5].
1.6.1. При каких условиях точка Торричелли
находится на пересечении зон влияния?
Точка находится
на пересечении зон Дирихле, если
,
а так как
,
значит
,
следовательно,
является равносторонним.
1.6.2.При каких условиях точка Торричелли
принадлежит зоне Дирихле вершины А?
Задание: найти условия на элементы треугольника, при которых выполняется система:
(1.2).
По теореме косинусов:
,
,
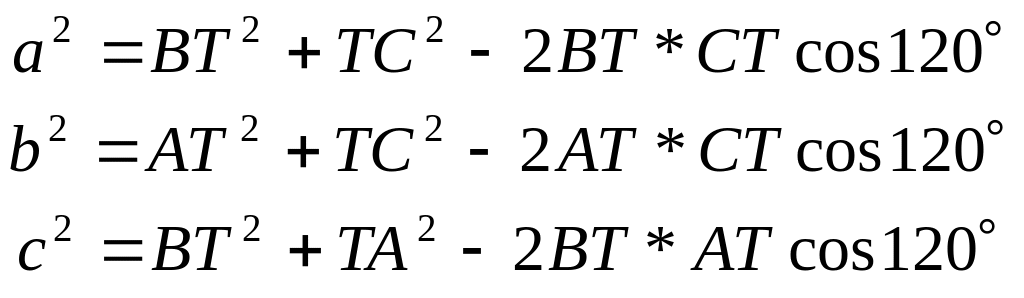значит
Пусть система (1.2) верна, тогда:
.
.
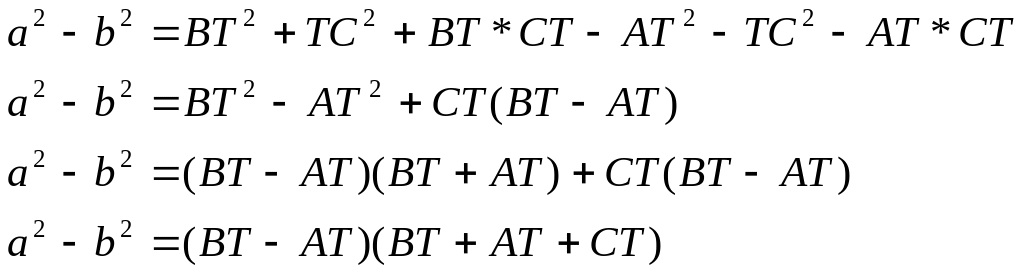
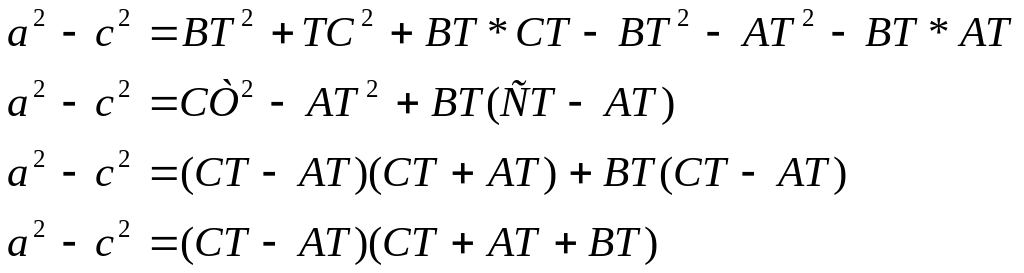
Значит система
(1.2) выполняется при
.
Вывод:
.
Теорема о принадлежности замечательных точек треугольника зонам Дирихле его вершин
Теорема. (О принадлежности замечательных точек треугольника зоне Дирихле его вершины). Центр описанной окружности всегда находится на пересечении зон Дирихле вершин треугольника. Ортоцентр, инцентр, центроид, точка Торричелли принадлежат зоне Дирихле вершины большего угла. Точки Брокара принадлежат зоне Дирихле вершины А, если выполняются соотношения:
, или .
Следствие (О принадлежности замечательных точек треугольника пересечению зон Дирихле его вершин ).
Условия
,
,
,
,
,
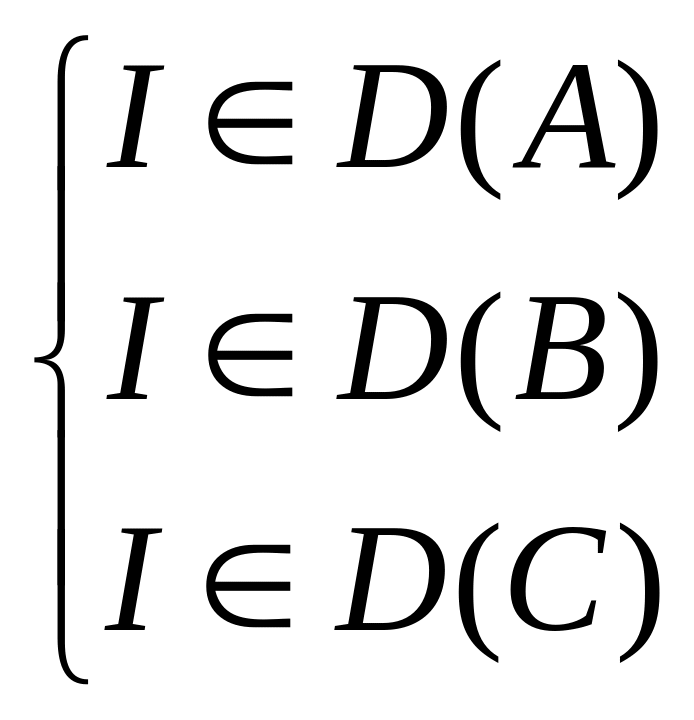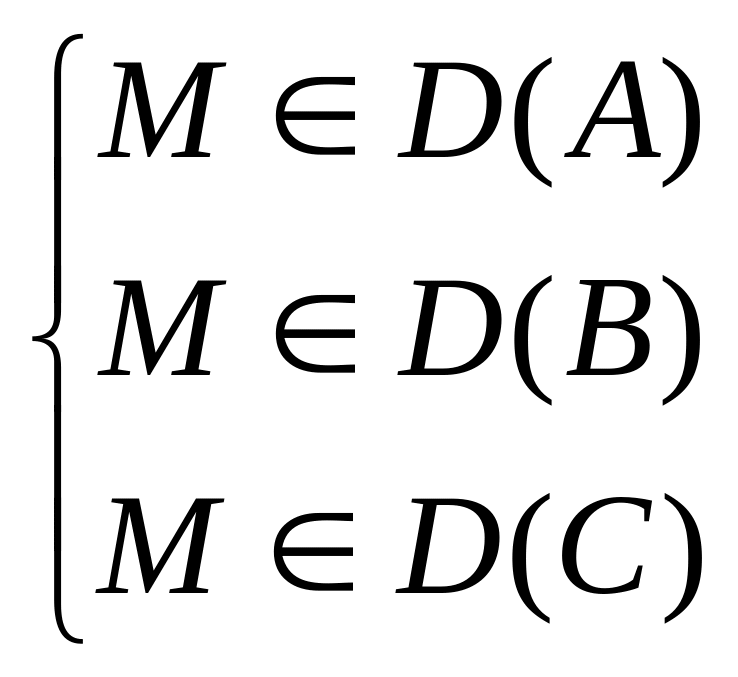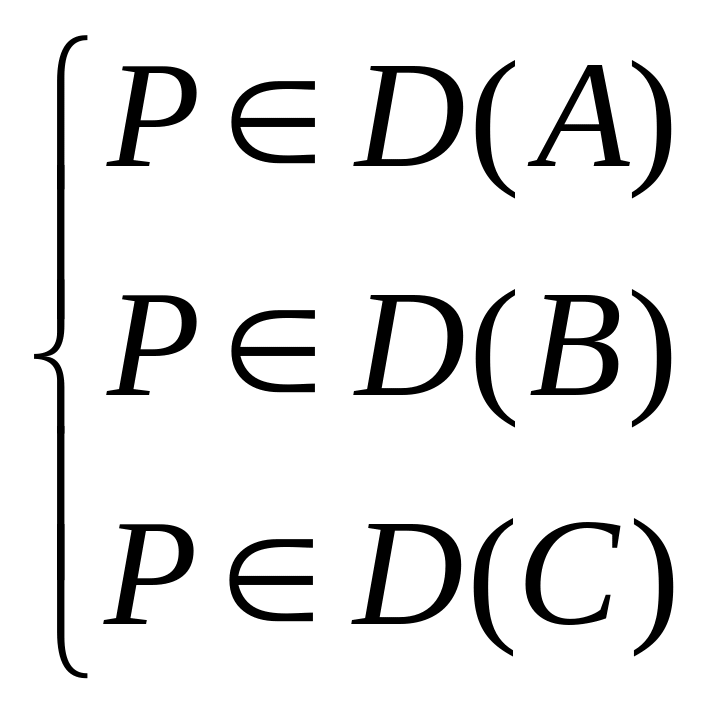верны
— правильный.