3. Центроид

Медиана треугольника ― отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны (рис. 1.5). Центроид — точка пересечения медиан в треугольнике. Точка пересечения медиан всегда лежит внутри треугольника.

1.3.1. При каких условиях центроид находится на пересечении зон Дирихле всех вершин треугольника?

Как для ортоцентра, центроид принадлежит зонам Дирихле всех вершин треугольника только в равностороннем треугольнике. Это следует из того, что медианы в равностороннем треугольнике являются высотами и центроид совпадает с центром описанной окружности.

1.3.2. При каких условиях центроид

принадлежит зоне Дирихле вершины А?

В треугольнике медиана находится по формуле

, , .

Это следует из тождества параллелограмма, согласно которому сумма квадратов диагоналей любого параллелограмма равна сумме квадратов всех его сторон. Известно, что центроидом медианы делятся на отрезки, которые относятся как 2:1, начиная от вершины треугольника. Имеем:

, , .

Будем искать условия на элементы треугольника, при которых , то есть выполняется система .

.

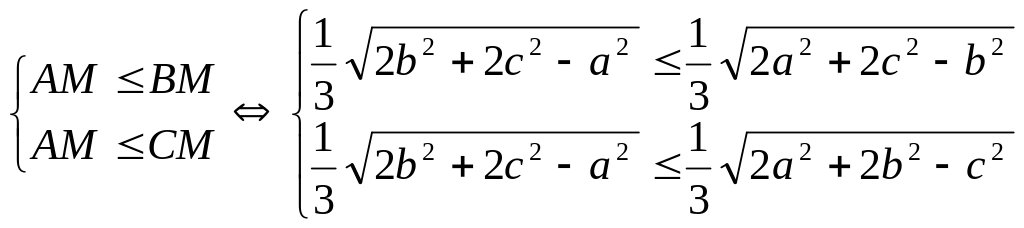Найдем условия на , , при которых эта система верна.

А) Первое неравенство верно тогда, и только тогда, когда

/возведём в квадрат

, ,

, , , выполняется при .

Б) Второе неравенство верно тогда, и только тогда, когда

/возведём в квадрат

, ,

, , , выполняется при .

Тогда система выполняется при .

Вывод: .

4. Инцентр

Биссектриса – луч, делящий угол пополам. Инцентр — точка пересечения биссектрис треугольника. Также инцентр является центром вписанной в треугольник окружности. Инцентр всегда лежит внутри треугольника.

1.4.1. При каких условиях инцентр

находится на пересечении зон Дирихле всех вершин треугольника?

Найдём условия на элементы треугольника, при которых инцентр совпадает с центром описанной окружности. Пусть они совпадают (рис 1.6).

Имеем , так как — центр описанной окружности , , — равнобедренные , , (как углы при основании равнобедренных треугольников). Так как , , — биссектрисы , то , то есть ( — равносторонний).

Инцентр лежит на пересечении зон Дирихле всех вершин треугольника в равностороннем треугольнике.

1.4.2. При каких условиях инцентр

принадлежит зоне влияния точки А?

Гипотеза: .

Доказательство

Точками касания окружность делит стороны треугольника на 6 частей (рис. 1.7), для которых выполняется система:

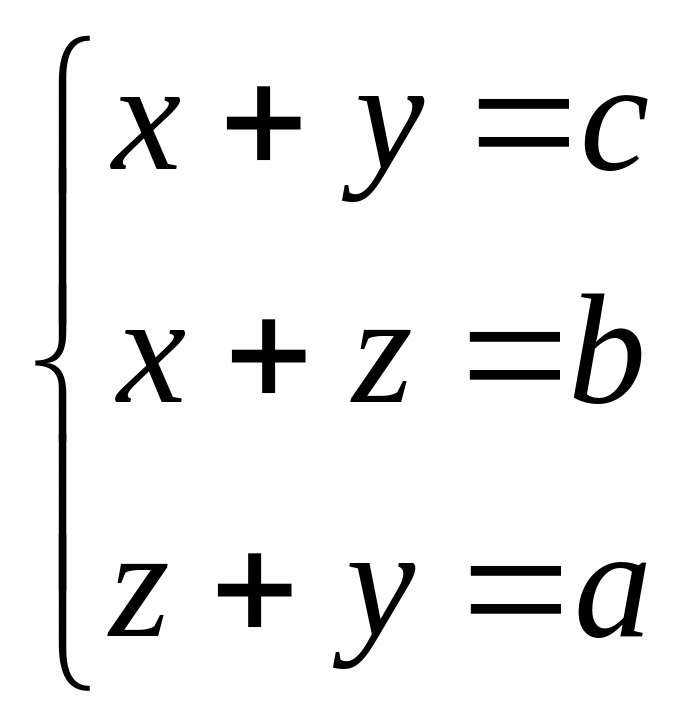(1.1)

Пусть , тогда .

Тогда 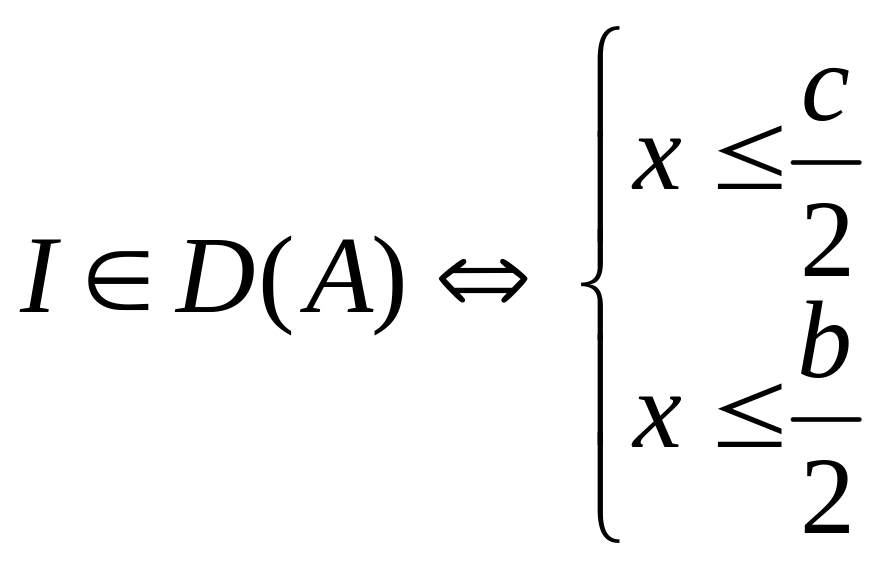, то есть проекции отрезка на , меньше, чем и соответственно. Преобразуем систему (1.1) : , , .

Далее , , , ,

или .

Так как то:

и .

Значит, .

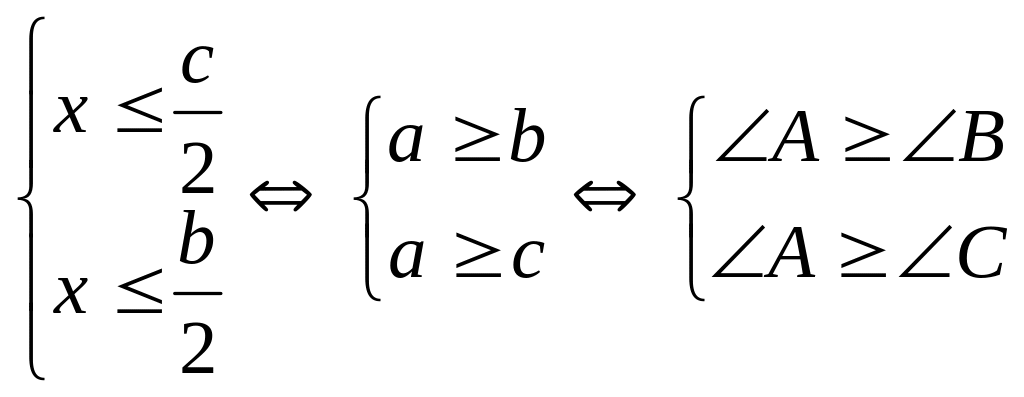Вывод: .

5. Точки Брокара

Точка Р, лежащая внутри , называется первой точкой Брокара (рис. 1.8), если . Точка Q, лежащая внутри , называется второй точкой Брокара (рис. 1.9), если .

Известно, что ([4, стр. 23]). Угол называют углом Брокара.