4.3.Частотно-монотонное планирование

Одним из эффективных методов планирования для периодических задач является частотно-монотонное плани­рование (rate monotonic scheduling — RMS). Система RMS назначает приоритеты заданиям на основе их периодов /13/.

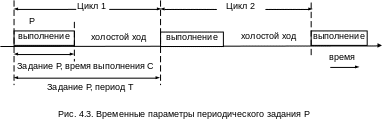
На рис. 4.3 представлены параметры периодических заданий. Пери­од задания Т представляет собой интервал времени между поступлениями двух последовательных заданий одного типа. Частота заданий, измеряемая в герцах, представляет собой величину, обратную периоду (в секундах). Например, зада­ние с периодом 50 ms имеет частоту 20 Гц. Обычно окончание периода задания является жестким предельным сроком завершения задания, хотя некоторые за­дания могут иметь и более ранние предельные сроки. Время выполнения (вычисления) С представляет собой количество процессорного времени, требую­щегося для каждого задания определенного типа. Очевидно, что в однопроцес­сорной системе время выполнения не должно превышать период заданий (т.е. должно выполняться ). Если периодическое задание всегда выполняется до полного завершения, т.е. если не имеется отклоненных из-за нехватки вычисли­тельного ресурса заданий, то загруженность процессора этим заданием равна U = С/Т. Например, если задание имеет период 80 ms и время выполнения 55 ms, то загруженность им процессора составляет 55/80 = 0,6875.

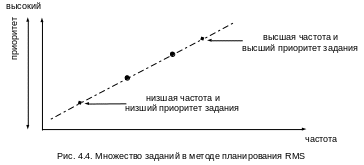
В частотно-монотонном планировании заданием с наивысшим приоритетом является задание с наименьшим периодом; вторым по приоритетности является задание со вторым по величине пе­риодом и т.д. Соответственно, в случае готовности для выполнения нескольких зада­ний первым обслуживается задание с наименьшим периодом. Если изобразить приоритеты заданий как функцию их частоты, то получается монотонно возрастающая функция (рис. 4.4), откуда и происходит название метода.

низкий

Одной из характеристик эффективности алгоритма периодического планирова­ния является его гарантия соответствия всем жестким предельным срокам. Предпо­ложим, что у нас имеется n заданий, каждое из которых имеет свое фиксированное время выполнения и период. Тогда необходимым условием соответствия всем жест­ким предельным срокам является выполнение следующего неравенства:

. (4.1)

Сумма загруженности процессора разными заданиями не может превышать единицу, что соответствует полной загрузке процессора. Неравенство (4.1) определяет верхнюю границу количества заданий, которые может успешно обслуживать идеальный алгоритм планирования. Для конкретного реального алгоритма гра­ница может оказаться ниже из-за затрат ресурсов процессора на планирование и диспетчеризацию. В /13/ показано, что для алгоритма RMS справедливо следующее неравенство:

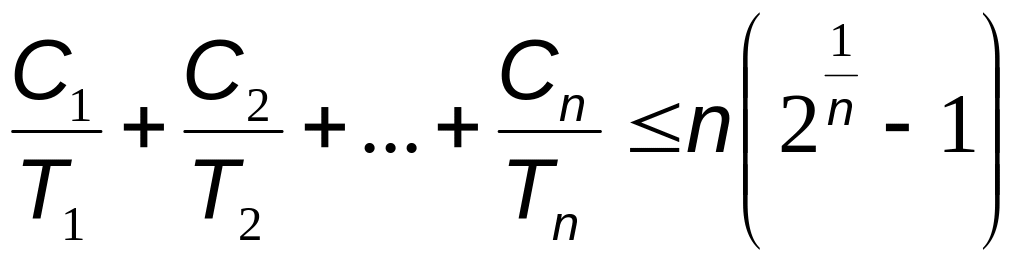. (4.2)

В табл. 4.3 приведены некоторые значения верхней границы загруженности процессора для метода RMS для разных значений n в (4.2). При возрастании количества заданий верхняя граница стремится к значе­нию In 2 =0,693.

Таблица 4.2

n
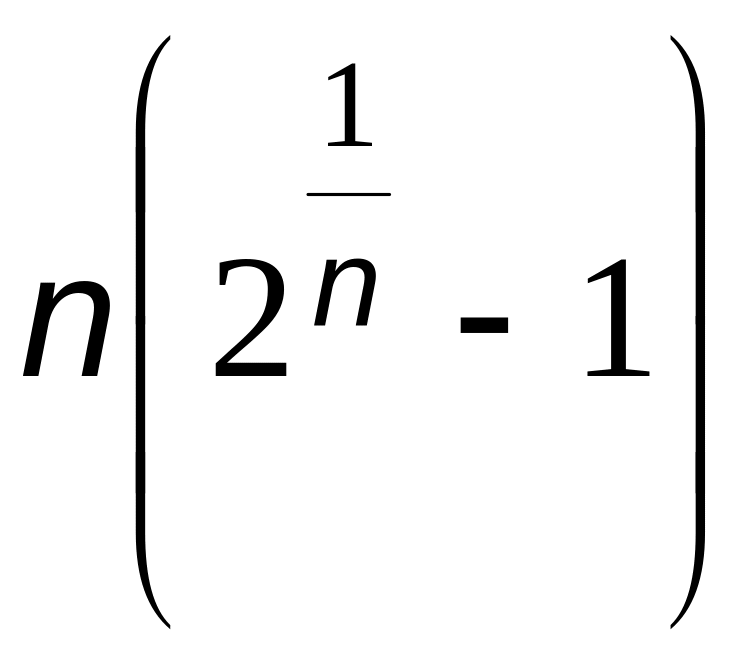
1	1.000
2	0.828
3	0.779
4	0.756
5	0.743
6	0.734
*	*
*	*

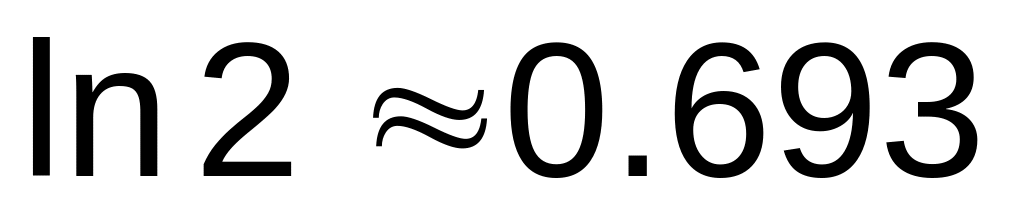
Пример 4.3. Произвести оценку возможности выполнения в реальном времени трех периодических заданий со следующими параметрами:

задание P₁: C₁ = 20; Т₁ = 100;

задание P₂: С₂ = 40; T₂ = 150;

задание Р₃: С₃ = 100; T₃= 350.

Загруженность процессора каждым из заданий составляет соответственно: U₁= 0,2; U₂= 0,267; U₃= 0,286. Тогда общая загруженность процессора тремя заданиями составляет U_o=0,2+0,267+0,286=0,753.

Верхняя граница загруженности этих трех задач при использовании метода RMS составляет:

.

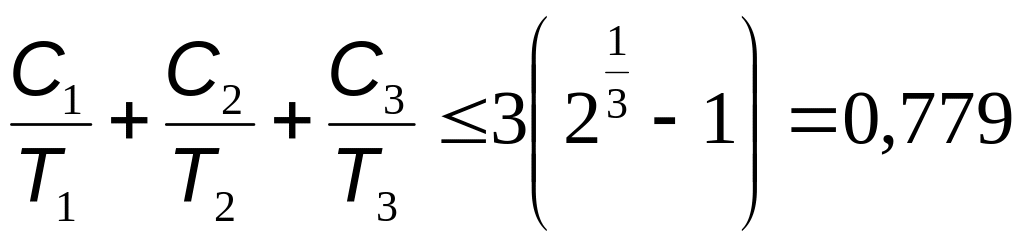Поскольку общая загруженность процессора по обработке приведенных за­даний ниже верхней границы для метода RMS (0,753<0,779), можно сделать вывод, что при RMS-планировании будут успешно выполнены все задания.

В /13/ указывается, что определяемая выражением (4.2) верхняя граница справедлива и для метода наиболее раннего предельного срока. Хотя при применении планирования с наиболее ранним предельным сроком можно достичь более высокой загрузки про­цессора и, соответственно, обработать большее количество заданий, ме­тод RMS широко распространен и используется во многих промышленных приложе­ниях.

Упражнение 4.1. Для группы периодических задач с заданным профилем построить временные диаграммы их выполнения для следующих алгоритмов планирования: с квантованием, относительными и абсолютными приоритетами, предельными сроками завершения и RMS.

Упражнение 4.2. Для группы непериодических задач с заданным профилем построить временные диаграммы их выполнения для следующих алгоритмов планирования: с заданными предельными сроками начала работы; предельными сроками начала и свободным временем простоя.

Для указанных упражнений определить возможность выполнения задач в реальном масштабе времени и рассчитать загруженность процессора. Число задач в группе и таблицы профилей задаются преподавателем.