ПОИСК АСИМПТОТИЧЕСКИХ РЕШЕНИЙ ЗАДАЧИ дробно-линейноГО программированиЯ

Общей задачей дробно-линейного программирования называется задача нахождения экстремума (максимума или минимума) функции

, () определенной на некотором выпуклом подмножестве n-мерного пространства, которое задается системой линейных уравнений и неравенств:

() Геометрический смысл и графический способ решение задачи

Рассмотрим на плоскости целевую функцию .

Выразим отсюда :

или где

Уравнение геометрически представляется прямой, проходящей через начало координат. При некотором фиксированном значении z угловой коэффициент прямой будет фиксирован и прямая займет определенное положение. Если изменить значение z, то изменится , и прямая повернется вокруг начала координат (рис.1).

Рис 1.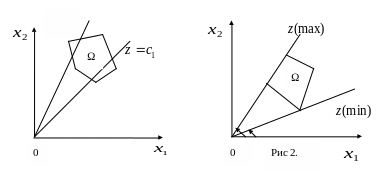

Установим, как будет есть себя угловой коэффициент при монотонном возрастании z. Для этого возьмём производную от по z

Знаменатель производной всегда положителен, а числитель от z не зависит. Следовательно, производная имеет постоянный знак, и при увеличении z угловой коэффициент будет или только возрастать, или только убывать, а прямая будет вращаться в одну сторону.

Обратно, при вращении прямой в одном направлении функционал z будет также или только увеличиваться, или только уменьшаться. Установив направление вращения для возрастания z, находим нужную вершину многогранника поворотом прямой вокруг начало координат.

Рис 3.

0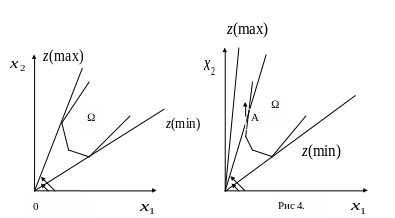

При этом возможны следующие различные случаи.

1.Многогранник ограничен, максимум и минимум есть (рис 2). Стрелки на рисунке показывают на направление, в котором надо вращать прямую для увеличения z.

2.Область не ограничена, но максимум и минимум имеются (рис 3).

3. Область не ограничена, и один из экстремумов не достигается (рис 4). При удалении точки A пересечение прямых в бесконечность, т.е. когда луч станет параллелен ребру многогранника, получается так называемый асимптотический максимум, который может быть как конечным так и бесконечно большим.

4. Область не ограничена, оба экстремума асимптотические (рис 5).

При увеличении размерности для фиксированного z из выражения функционала получаем гиперплоскость, проходящую через начало координат:

Для переменного z это будет пучок гиперплоскостей; при изменении z гиперплоскость вращается вокруг оси пучка, задевая вершины многогранника. Таковы геометрический смысл задачи и основанный на нем графический метод ее решения.

Пример. Найти максимум и минимум функционала

при ограничениях:

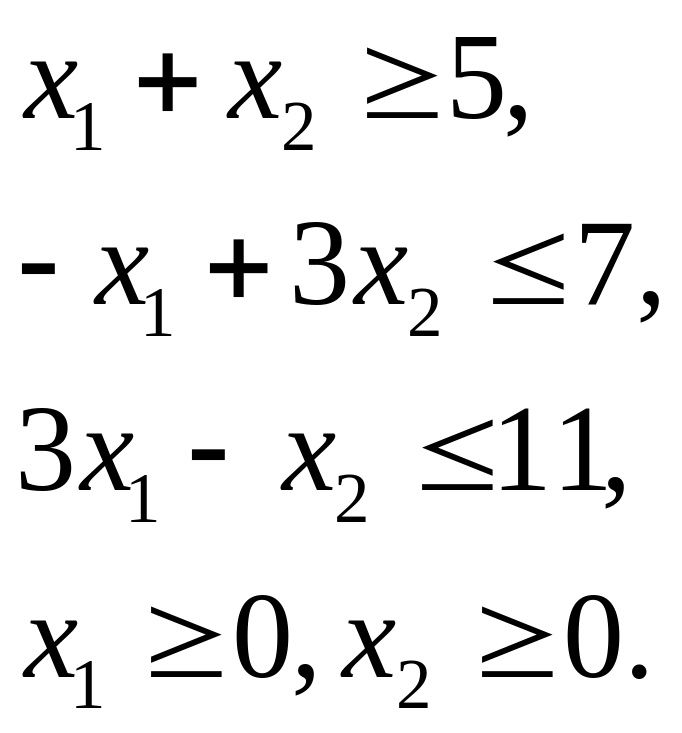
Строим на чертеже в определенном масштабе область решения задачи (рис 6). Так как оптимум находится вращением разрешающей прямой вокруг начало координат, сразу можно сказать, что экстремальными точками будут вершины A и В.

0

Рис 5.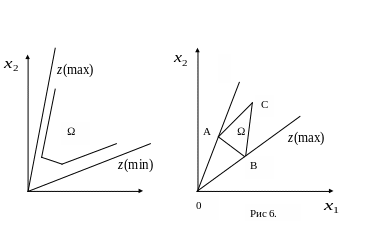

Чтобы определить, где будет минимум, а где максимум, можно воспользоваться приведенными выше рассуждениями.

Выразим из целевой функции :

Угловой коэффициент разрешающей прямой

.

Ищем производную:

Так как производная при любом z отрицательна, функция убывающая, с увеличением z угловой коэффициент уменьшается. Это соответствует прямой по часовой стрелке . Следовательно, в вершине A значение функционала будет наименьшим,

в вершине B – наибольшим (рис 6).

Практически же дело обстоит гораздо проще. Определи по рисунку экстремальные точки, из решения соответствующих уравнений получим их координаты, которые так или иначе необходимы: Затем вычисляем нужные нам значение функционала в этих точках:

Поскольку , заключаем, что вершине A будет минимум, а вершине B – максимум.

Поиск с помощью метода Штифеля асимптотических решений задачи дробно – линейного программирования

Дана задача: найти максимум функционала (1)

При выполнении ограничений:

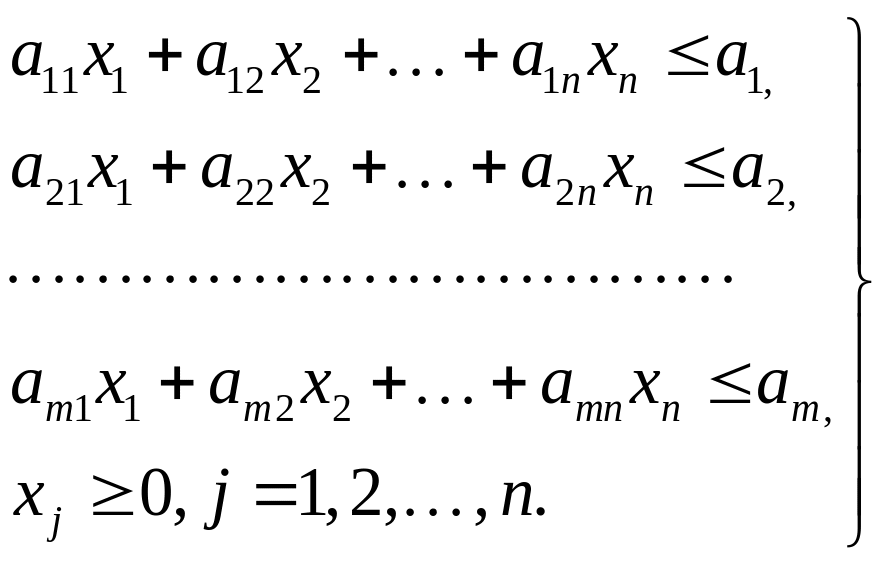(2)

Решение задачи выполняется в такой последовательности.

1.Составим жорданову таблицу. При этом для функционала предусмотрены две строки: в верхнюю записываем коэффициенты числителя, а в нижнюю – знаменателя (таб.1).

2. Если записанный в таблице план не является опорным, т.е. среди свободных членов есть отрицательные, то шагами модифицированных жордановых исключений отыскиваем опорный план, подвергая при этом всем преобразованиям и коэффициенты строк и .

В результате шагов придем к следующей таблице.

В этой таблице все свободные члены не отрицательны. В строках для и появятся свободные члены и , в общем случае отличны от нуля ( всегда будет отлично от нуля по условию положительности знаменателя в многогранники решений).

Как и в случае линейного программирования, решение, записанное в таблице, получаем, приравнивая все верхние переменные нулю, а боковые – свободным членам. Так находится вершина многогранника. При этом значение функционала на k-м шаге

Рассмотрим отыскания оптимального решения, т.е. максимум функционала . Для этого надо перемешаться из полученной вершины по какому-то ребру в соседнюю вершину многогранника, расположенную ближе к оптимальной вершине. Аналитически надо делать следующий шаг модифицированных жордановых исключений с некоторым разрешающим элементом . Задача заключается том, чтобы установить правило выбора этого элемента.

Итак, пусть разрешающим будет элементом . В новой -й таблице на месте числа будет стоят число аналогично вместо числа будем иметь Значение функционала на -м шаге будет рано отношению этих новых чисел: 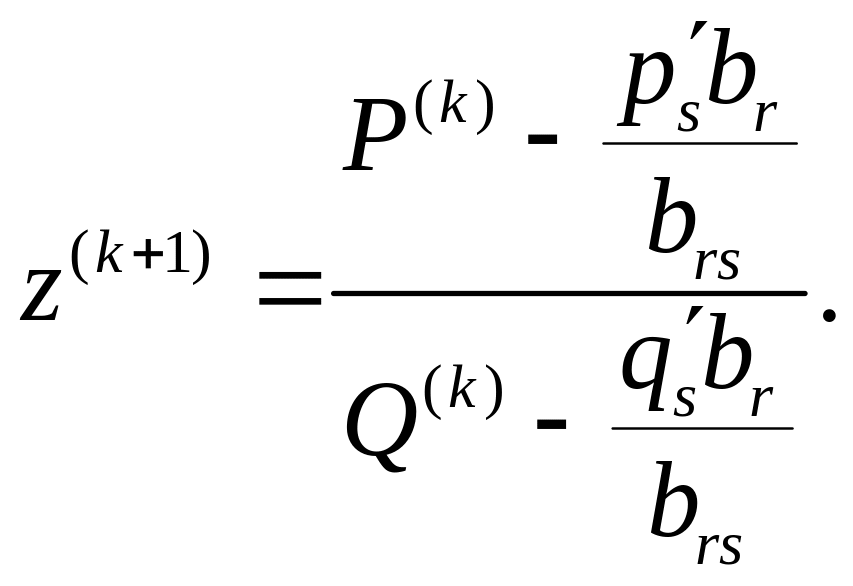Найдем разность полученного и предшествующего значений функционала: 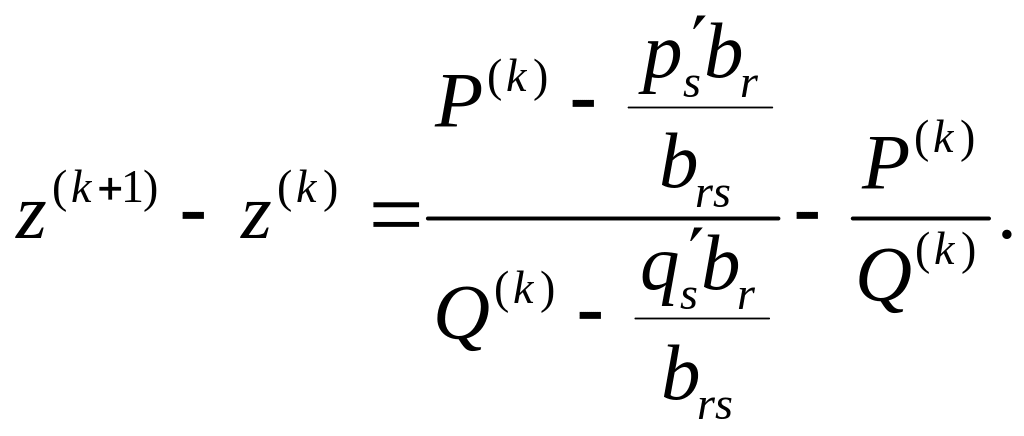Приводим дроби к общему знаменателю:

Приведем подобные члены, вынесем в числители общий множитель со знаком минус за скобку, а знаменатели заменим выражение в скобках на . Получим:

Обозначим числитель первой дроби символом :

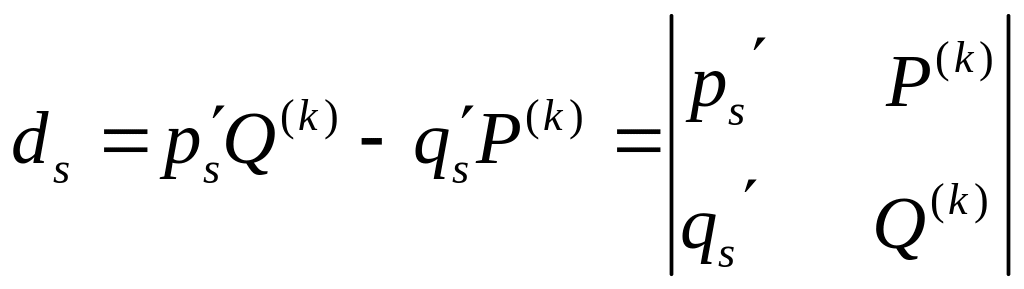(3)

Это будет так называемый определитель второго порядка с элементами и - строк, стоящими столбце s и в столбце свободных членов табл.2. С этим обозначением будем иметь

(4)

Исследуем выражение (4).

1.Чтобы не оторваться от многогранника решений, симплексное отношение должно быть положительным и минимальным из всех возможных:

(отсюда должно быть , так как по условию допустимости плана ). Следовательно, скобка в выражении (4) всегда будет отрицательной: .

2. Так как по условию знаменатель функционала в области решений всегда положителен, т.е. для любого плана , то оба сомножителя в знаменателе первой дроби будут всегда положительны. Поэтому знак разности зависит от знака определителя .

Если этот определитель положителен: , то вся правая часть выражения (4) окажется отрицательной, т.е. будем иметь ; отсюда .

Иными словами, если за разрешающий взять столбец с положительным , то после шага жордановых исключений значение функционала уменьшиться.

Если определитель будет отрицательным: , то правая часть выражения (4) станет положительной: , отсюда , т.е. значение функционала на очередном шаге в этом случае увеличится.

Если будет , то , , т.е. значение функционала останется без изменения.

Определитель и служит критерием для выбора разрешающего столбца.

Имея такие результаты, для отыскания оптимального плана можно сформулировать следующие пункты алгоритма.