Лабораторна робота 7 Частотний аналіз

1. Опис методу криптоаналізу

Всі природні мови мають характерний задокументований частотний розподіл літер, отже, шифри моноалфавітної заміни (наприклад, шифр Цезаря) можуть бути розкриті за допомогою методу статистичного аналізу – частотного аналізу.

Для того, щоб отримати відкритий текст, необхідно співставити частоти символів шифротексту з відомими ймовірностями символів алфавіту, що використовується. Якщо – довжина шифротексту, – кількість літер «А» в шифротексті, то під частотою символу «А» розуміють відношення:

.

Після того, як обчислені частоти всіх символів шифротексту, символи з найбільшою частотою замінюють на відповідні найбільш ймовірні символи алфавіту. При цьому також враховуються найбільш ймовірні сполучення з двох символів (біграми), трьох символів (триграми), слова та синтаксичні правила вихідної мови.

2. Завдання на проведення лабораторної роботи

Дешифрувати шифротекст (файл «…Задания ЛР07\СText*.txt», де * − номер варіанту) за допомогою частотного аналізу. Для дешифрування можна використовувати програму FA.exe (рис. 7.1).

Рисунок 7.1 – Програма FA.exe

Порядок роботи з програмою:

1. Кнопка «Открыть текст» – відкрити текст, що аналізується (шифротекст). За замовченням файл «CText*.txt».

2. Кнопка «Вычислить» – обчислює частоти тексту, що аналізується, виводить таблицю частот.

3. Кнопка «Исх.текст» – відкрити файл частот вихідного тексту (відкритого тексту). За замовченням файл «SymbTableSource.txt».

4. Кнопка «Подставить» – замінює символи шифротексту відповідно до підстановки (відсортовані за спаданням стовпці «Ан.текст» та «Исх.текст»).

5. Якщо після підстановки залишились неточно замінені символи, використовується кнопка «Заменить».

6. Результуюча підстановка зберігається в файлі «result.txt».

У звіті з лабораторної роботи необхідно навести дешифрований текст та результуючу підстановку.

Лабораторна робота 8 Криптоаналіз шифру Віженера з періодичним ключем

1. Теоретичні відомості

Нехай – скінчена група. Розглянемо шифросистему . Інформація представляється послідовністю . Сеансовий ключ – (потенційно нескінчена) періодична послідовність – «гамма», тобто накладається на інформацію, що генерується, за допомогою порозрядної групової операції . Таким чином, шифротекст має вид

,

де . Такий шифр називають іноді шифром Віженера (або шифром Вернама).

Криптоаналіз шифросистеми може бути здійснений у відповідності до такої схеми, що складається з двох етапів: на 1-у етапі обчислюється період сеансового ключа , а на 2-у етапі – сам сеансовий ключ .

1-й етап (тобто обчислення періоду сеансового ключа) здійснюється у відповідності до методу Ф. Казіскі (1863р.):

Два однакових відрізка відкритого тексту, що відстоять один від одного на відстані , зашифровані однаково.

Індексом збігу в послідовності називається ймовірність того, що збігаються два випадково обраних елементи цієї послідовності. Цей індекс обчислюється у відповідності до формули:

,

де – число входжень елементу в послідовність .

Нехай – ймовірність появи елементу в осмисленому тексті. Тоді

для будь-якого осмисленого тексту .

За допомогою цієї формули можуть бути підраховані індекси збігу в осмисленому тексті для будь-якої природної мови. Для деяких європейських мов такі індекси наведені в таблиці 8.1.

Таблиця 8.1

Мова	Російська	Англ.	Франц.	Нім.	Італ.	Іспан.
	0.0529	0.0662	0.0778	0.0762	0.0738	0.0775

Обчислення періоду сеансового ключа здійснюється в такий спосіб. Представимо шифротекст в виді матриці

.

Якщо , то для кожного стовпця матриці

,

оскільки кожний стовпець матриці – це результат застосування фіксованої циклічної перестановки , визначеної на множині .

Якщо ж , то

,

де – індекс збігу у випадковому тексті природної мови, яка використовується.

Оскільки для будь-якої природної мови , то обчислення періоду сеансового ключа не складає особливих зусиль.

2-й етап (тобто обчислення сеансового ключа при відомому його періоді ) здійснюється в такий спосіб.

Взаємним індексом збігу в послідовностях і називається ймовірність того, що випадково обраний елемент послідовності збігається з випадково обраним елементом послідовності . Взаємний індекс збігу в послідовностях і обчислюється у відповідності до формули:

,

де – число входжень елементу в послідовність . Оскільки період сеансового ключа відомий, то відома матриця

,

де кожний стовпець отриманий в результаті застосування фіксованої циклічної перестановки , що визначена на множині .

Розглянемо аналіз матриці , якщо , де для всіх . Кожна циклічна перестановка має вид

,

тобто представляє собою відносний зсув на величину . Звідси витікає, що

,

де – ймовірність появи елементу в відкритому тексті. А оскільки

,

то стовпці і з відносними зсувами на величини і мають однакові взаємні індекси збігу. По аналогії з індексами збігу, взаємні індекси збігу при зсуві на величину можуть бути обчислені для будь-якої природної мови.

Нехай – стовпець, який отримано в результаті додавання (по модулю ) елемента до кожного елемента стовпця . За допомогою формули

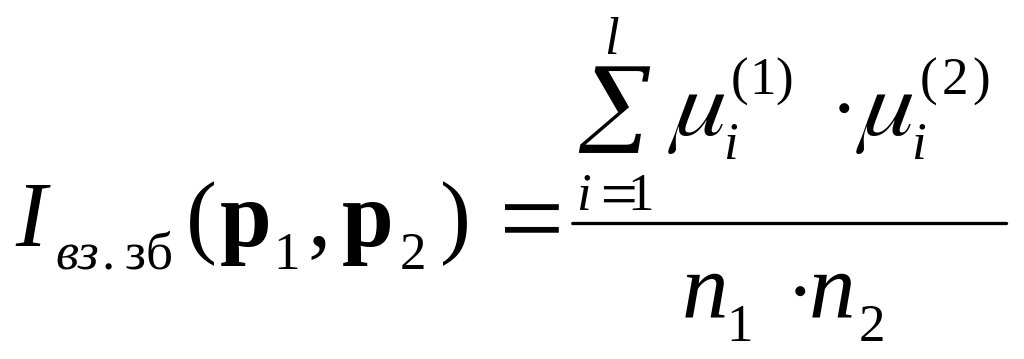
можуть бути обчислені значень . Якщо , то близько до взаємного індексу збігу при зсуві на величину для природної мови, що використовується, а якщо , то істотно відрізняється від цього індексу, тобто обчислення сеансового ключа зводиться до пошуку розв’язків системи лінійних рівнянь

.

2. Завдання на проведення лабораторної роботи

Для шифротексту (файл «…Задания ЛР08\CText*.txt», де * − номер варіанту) визначити період сеансового ключа (1-й етап криптоаналізу) та відновити ключ (2-й етап).