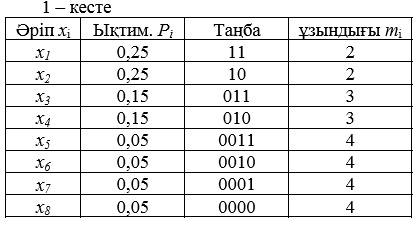
18. Шеннон- Фано әдісінің этаптары

19. Хаффман әдісі.

Хаффман әдісі бойынша файлды қысу үшін, біріншіден, файлды толығымен оқып және әр символ қанша рет кездесетінін есептеп шығу керек. Символдардың кездесу жиілігін санағансоң, жиілігі төмендеу бойынша топтастырылады, яғни кестедегі әр символдың орнын ауыстырмай жадыда сілтеме кестесі төмендеу бойынша сортталады. Соңғы кестедегі әр сілтемені “түйін”-деп атаймыз. Мұнан былай (ағашта) осы “түйінге” көрсететін сілтемені орналастырамыз.

Мысал Ұзындығы 100 байт мәтіндік файлды қарастырайық. Мәтін әртүрлі 11 символдан тұрсын. Әр символдың кездескен санын (кіріс жиілігін) есептеп келесіні алдық. 3.2-кесте

символ	а	о	ғ	к	ы	т	ү	і	п	е	д
кіріс саны	12	22	7	10	3	6	11	8	6	9	6

Ыңғайлық үшін символдар мен олардың кіріс жиілігін былай құрастырамыз:

Енді жиілігі ең аз екі символды аламыз: біздің мысалымызда бұл “ы” (3) және “т” (6) немесе “п”, “д” (6), соңғы үш символдардың кез келгенін алуға болады. Біз “т” символды алайық. “ы” және “т” түйіндерден жаңа түйін құрастырамыз, оның жиілігі “ы” және “т” жиіліктерінің сомасына тең.

Шеңбер ішіндегі номер – “ы” және “т” символдар жиіліктерінің сомасы. Енді қайтадан ең аз жиілікті екі символды іздейміз.Осылай жалғастырып, толық “ағашты” құрастырамыз, яғни бір түйінге барлығы жиналу қажет. Ағашды құрғаннан кейін біз файлды таңбалай аламыз. Әрқашан ағаштың түбірінен (Root) бастауымыз керек. Символға таңба бергенде ағаш бойымен жоғарыға қарай жүріп, бұтақтардың барлық бұрылысын ескереміз, егер солға бұрылсақ, онда 0 таңбасын сақтаймыз және 1 таңбасын – оң бұрылысқа. “а” символ үшін таңбаны беру жолын қарастырайық: оңға 57-ге қарай жүреміз (1-ді сақтаймыз), енді сол бұрыс, сосын тағы сол бұрыс жасаймыз. “а” үшін таңба – 101. “ғ” символды қарастырсақ – оң, оң, сол, сол, яғни 1100 таңбасын аламыз. Осылай барлық символдар үшін орындаймыз:

3.3-кесте

символ	таңба	ұзындығы, бит
а о	101 00	3 2

Файлдың алғашқы мөлшері: 100 байт – 800 бит;

Сығылғын файлдың мөлшері: 41,5 байт – 332 бит

Файл 58,5 %-ға сығылды.

Мұның бәрі өте жақсы, бірақ алғашқы файлды қайтару үшін таңбаны шешетін ағаш қажет, әр файлға ағаштар өзгеше болғандықтан. Сондықтан ағашты файлмен бірге сақтау керек. Бұл нәтижесінде соңғы файлдың мөлшерін ұлғайтады.

20. Арифметикалық кодтау.

Арифметикалық таңбалауда мәтiн 0-ден 1-ге дейiн аралықта жататын заттық сандармен берiледi. Мәтiндi таңбалау барысында оны көрсететiн аралық азаяды, ал биттер саны өседi. Белгiлi бiр модельмен берiлген ықтималдылығына байланысты мәтiннiң келесi символдары аралықтың шамасын қысқартады. Ықтималдылығы аз символдарға қарағанда, ықтималдылығы көп символдар аралықты азырақ қысқартады, сондықтан олар нәтижиеге аз бит қосады. Жұмыстың басында мәтiнге лайық аралығымыз – [0; 1). Келесi символды өңдегенде, оған аралықтың бөлiгiн бергеннен соң аралықтың иенi тарылады. {a, e, i, o, u, !} алфавиті (әріпердің ықтималдылықтары тұрақты) берілсін. “eaii!” мәтiнiн таңбалайық.

символ	ықтималдылық	аралық
a e i o u !	0.2 0.3 0.1 0.2 0.1 0.1	[0.0; 0.2) [0.2; 0.5) [0.5; 0.6) [0.6; 0.8) [0.8; 0.9) [0.9; 1.0)

Таңбалаушыға (кодировщик) да, таңбаны шешушiге (декодировщик) де ең бастапқы аралық [0; 1) екендiгi белгiлi. Келесі [L; H) жұмыс аралығын анықтағанда мына формуланы қолданамыз: мұнда L_ж – ағымды жұмыс аралығының бастапқы мәні, h_ж – ағымды жұмыс аралықтың қадамы, l_c1, l_c2 – символға берілген (кестедегі) аралықтың сәйкесінші бастапқы және соңғы мәні.

Таңбалау жолдар: Басында жұмыс аралығымыз – [0; 1), бастапқы символымыз (“eaii!” мәтiнi үшін) – “е”-ні қарастырамыз: [0 + 1*0.2; 0 +1*0.5) = [0.2; 0.5).

1-шi символ "е"-нi қарастырғаннан кейiн, таңбалаушы аралықты, осы символға модель бойынша берiлген, [0.2; 0.5)-ке дейiн тарылтырады. Енді жұмыс аралығымыз – [0.2; 0.5). h_ж қадамы 0.3 тең. “а” символды қарастырғаннан соң:

“а”: [0.2+0.3·0; 0.2+0.3·0.2) = [0.2; 0.26), h_ж = 0.06;

“i”:[0.23; 0.236); “i”:[0.233; 0.2336); “!”:[0.23354; 0.2336).

Таңбаны шешушiнiң мәтiн туралы тек оның соңғы аралығын [0.23354; 0.2336) бiледi деп болжайық. Декадировщикке қорытынды аралықтың екi шектiң мәндерiн мiндеттi түрде бiлу қажет емес. Тiптi аралықтың iшiнде жатқан бiр мәннiң өзi, мысалы 0.23355, жеткiлiктi. (Басқа сандар – 0.23354, 0.23357 немесе 0.23354321 – әбден жеткiлiктi). Бiрақ процестi аяқтау үшiн, декодировщик мәтiннiң соңын дәл табу керек. Сондықтан мәтiннiң аяғын арнайы символмен белгiлеу керек, кодировщик және декодировщикке белгiлi. Осы мақсатқа кестедегi “!” символы қолданылады. Осы символды декодировщик кездестiргенде өз процесiн аяқтайды. 3.5-шi кесте бойынша модельдiң “е” символға берiлген аралық қорытынды аралықта толығымен жатқандықтан, ол бiрiншi кодталған cимволдың осы екендiгiн бiрден түсiнедi. Осы аралықтағы кез-келген санды жіберуге болады. Ендi декодировщиктiк әрекетiн қайталайық:

Басында [0.0; 1.0)

“е”-ні қарастырғаннан кейiн [0.2; 0.5)

Екiншi символ "а" екенi түсiнiктi, ол [0.2; 0.26) аралыққа әкеледi, [0.23354; 0.2336) қорытынды аралық толығымен iшiнде жатқаннан соң. Осылай жалғастыра бере декодировщик мәтiндi шығарып алады.

Бұл қадамдарды мына теңсіздікпен алуға болады. l_c1≥ (value-L)/h < l_c2, value – алынған код.