Вольтамперная характеристика тиристора

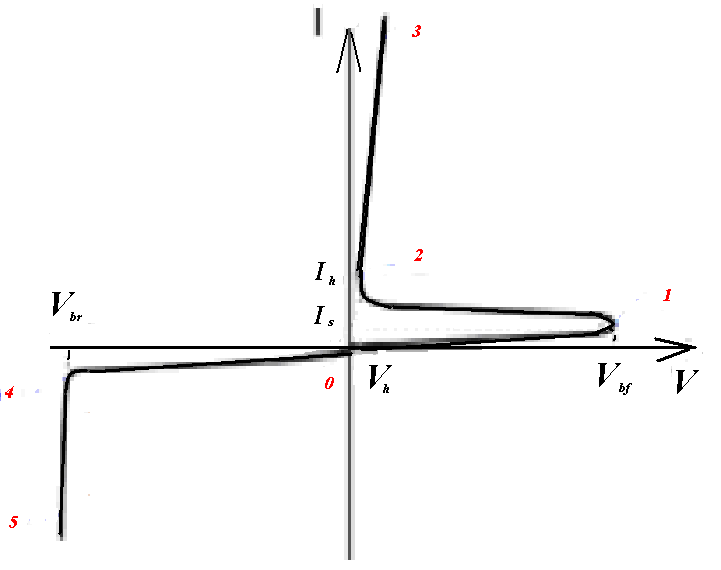
Рис.  Вольтамперная характеристика тиристора

Типичная ВАХ тиристора, проводящего в одном направлении (с управляющими электродами или без них), приведена на рис 2. Она имеет несколько участков:

Между точками 0 и 1 находится участок, соответствующий высокому сопротивлению прибора — прямое запирание. В точке 1 происходит включение тиристора. Между точками 1 и 2 находится участок с отрицательным дифференциальным сопротивлением. Участок между точками 2 и 3 соответствует открытому состоянию (прямой проводимости). В точке 2 через прибор протекает минимальный удерживающий ток I_h. Участок между 0 и 4 описывает режим обратного запирания прибора. Участок между 4 и 5 — режим обратного пробоя. Вольтамперная характеристика симметричных тиристоров отличается от приведённой на рис. 2 тем, что кривая в третьей четверти графика повторяет участки 0—3 симметрично относительно начала координат.По типу нелинейности ВАХ тиристор относят к S-приборам.

Современные тиристоры изготовляют на токи от 1 мА до 10 кА; на напряжения от нескольких В до нескольких кВ; скорость нарастания в них прямого тока достигает 10⁹ А/сек, напряжения — 10⁹ В/сек, время включения составляет величины от нескольких десятых долей до нескольких десятков мкс, время выключения — от нескольких единиц до нескольких сотен мкс; кпд достигает 99 %.

Тиристороры в электронной технике применяются как электронные ключи, управляемые выпрямители, преобразователи (инверторы), регуляторы мощности

3.2.4 Заключительная часть занятия (5 мин.).

1. подвести итоги;

2. выдать задание на самоподготовку;

3. ответить на вопросы.

Занятие 3. Логические элементы, назначение и применение в электронике.

Изучаемые вопросы:

1. Организационная часть занятия (2 мин.).

2. Логические элементы их применение в электротехнике (10 мин.).

3. Теоретические основы работы логических элементов (30мин.).

4. Заключительная часть занятия (3 мин.).

3.3.1 Организационная часть занятия

1. проверить количество курсантов;

4. довести краткие сведения о транзисторах и тиристорах, их применении в современной технике.

3.3.2 Логические элементы их применение в электротехнике

Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность "0", "1" и "2" в троичной логике, последовательности "0", "1", "2", "3", "4", "5", "6", "7", "8"и "9" в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.

С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже - на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана о экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами. Логические элементы выполняют логическую функцию (операцию) с входными сигналами (операндами, данными).

3.3.3 Теоретические основы построения логических элементов

Математической основой цифровой электроники и вычислительной техники является алгебра логики или булева алгебра (по имени английского математика Джона Буля).

В булевой алгебре независимые переменные или аргументы (X) принимают только два значения: 0 или 1. Зависимые переменные или функции (Y) также могут принимать только одно из двух значений: 0 или 1. Функция алгебры логики (ФАЛ) представляется в виде (данная форма задания ФАЛ называется алгебраической): 

Y = F (X1; X2; X3 ... XN ).

Основными логическими функциями являются:

- логическое отрицание (инверсия)

  Y = ;

- логическое сложение (дизьюнкция)

  Y = X1 + X2  или  Y = X1 V X2 ;

- логическое умножение (коньюнкция)

  Y = X1 · X2   или  Y = X1 L X2 .

К более сложным функциям алгебры логики относятся:

- функция равнозначности (эквивалентности)

  Y = X1 · X2 +  или Y = X1 ~ X2 ;

- функция неравнозначности (сложение по модулю два)

  Y = X1 ·  + · X2  или Y = X1  X2 ;

- функция Пирса (логическое сложение с отрицанием)

  Y =  ;

- функция Шеффера (логическое умножение с отрицанием)

  Y =   ;

Для булевой алгебры справедливы следующие законы и правила:

- распределительный закон

  X1 (X2 + X3) = X1 · X2 + X1 · X3 ,

  X1 + X2 · X3 = (X1 + X2) (X1 + X3) ;

- правило повторения

  X · X = X , X + X = X ;

- правило отрицания

  X ·  = 0 , X +  = 1 ;

- теорема де Моргана

   =  ,     =  ;

- тождества

  X · 1 = X ,  X + 0  = X ,  X · 0 = 0 ,  X + 1 = 1.

Схемы, реализующие логические функции, называются логическими элементами. Основные логические элементы имеют, как правило, один выход (Y)  и несколько входов, число которых равно числу аргументов (X1;X2;X3 ... XN ). На электрических схемах логические элементы обозначаются в виде прямоугольников с выводами для входных (слева) и выходных (справа) переменных. Внутри прямоугольника изображается символ, указывающий функциональное назначение элемента.

На рис. представлены логические элементы, реализующие рассмотренные в п.2.2. функции. Там же представлены так называемые таблицы состояний или таблицы истинности, описывающие соответствующие логические функции в двоичном коде в виде состояний входных и выходных переменных. Таблица истинности является также табличным способом задания ФАЛ.

На рис. представлен элемент “НЕ”, реализующий функцию логического отрицания Y = .

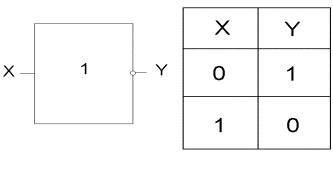
Рис.

Элемент “ИЛИ” (рис.2) и элемент “И” (рис.3) реализуют функции логического сложения и логического умножения соответственно.

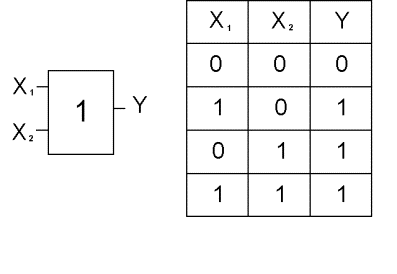
Рис.

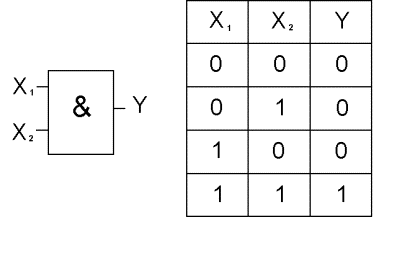
Рис. 3

Функции Пирса и функции Шеффера реализуются с помощью элементов “ИЛИ-НЕ” и “И-НЕ”, представленных на рис.4 и рис. 5 соответственно.

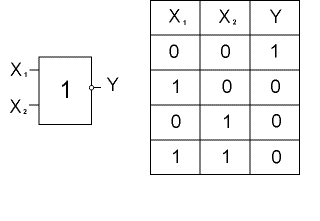
Рис.

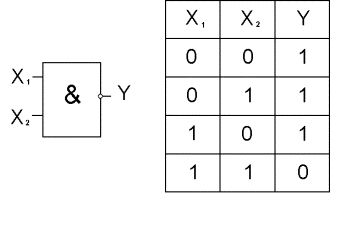
Рис.

Элемент Пирса можно представить в виде последовательного соединения элемента “ИЛИ” и элемента “НЕ” (рис.6), а элемент Шеффера  - в виде последовательного соединения элемента “И” и элемента “НЕ” (рис.7).

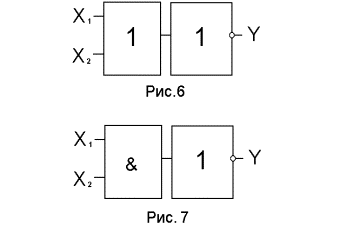
На рис.8 и рис.9 представлены элементы “Исключающее ИЛИ” и “Исключающее ИЛИ - НЕ”, реализующие функции неравнозначности и неравнозначности с отрицанием соответственно.

Рис.

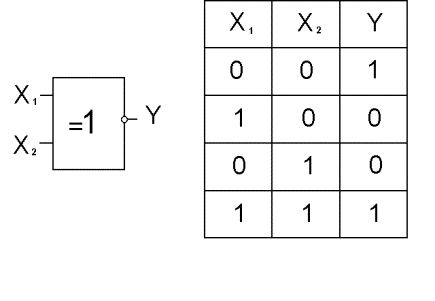
Рис.

Логические элементы, реализующие операции коньюнкции, дизьюнкции, функции Пирса и Шеффера, могут быть, в общем случае, n - входовые. Так, например, логический элемент с тремя входами, реализующий функцию Пирса, имеет вид, представленный на рис.10.

 

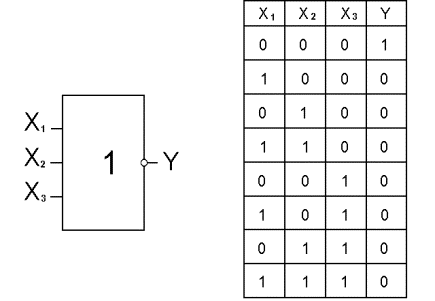
Рис.

В таблице истинности (рис. ) в отличие от ранее приведенных таблиц имеется восемь значений выходной переменной Y. Это количество определяется числом возможных комбинаций входных переменных N, которое, в общем случае, равно:   N = 2 n , где  n - число входных переменных.

Логические элементы используются для построения интегральных микросхем, выполняющих различные логические и арифметические операции и имеющих различное функциональное назначение. Микросхемы типа К155ЛН1 и К155ЛА3, например, имеют в своем составе шесть инверторов и четыре элемента Шеффера соответственно (рис.11), а микросхема К155ЛР1 содержит элементы разного вида (рис.12).

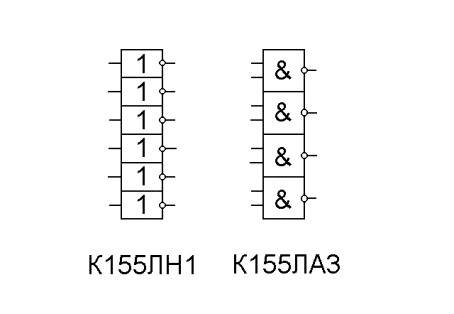
Рис.

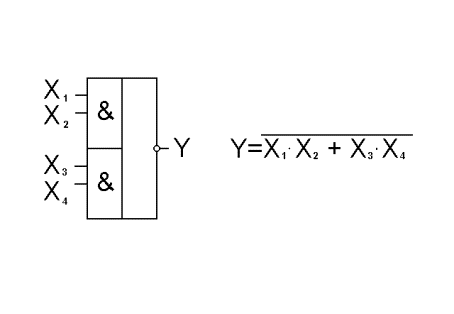
Рис.

ФАЛ любой сложности можно реализовать с помощью указанных логических элементов. В качестве примера рассмотрим ФАЛ, заданную в алгебраической форме, в виде:

.        (1)

Упростим данную ФАЛ, используя вышеприведенные правила. Получим:

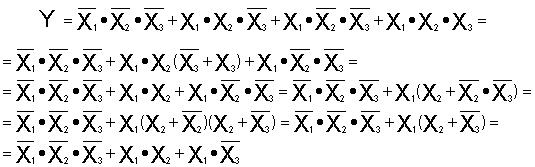   (2)

Проведенная операция носит название минимизации ФАЛ и служит для облегчения процедуры построения функциональной схемы соответствующего цифрового устройства.

Функциональная схема утройства, реализующая рассматриваемую ФАЛ, представлена на рис.13.

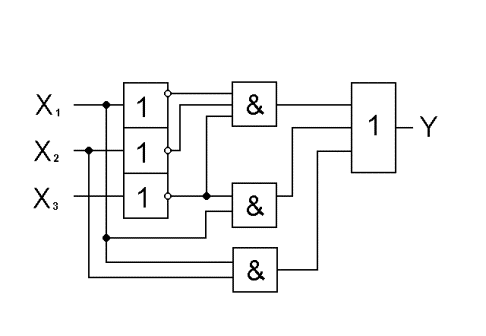
Рис.

Следует отметить, что полученная после преобразований  функция не является полностью минимизированной.