2.2 Проектирование тороидального резонатора.

В пролетных клистронах средней сантиметрового и коротковолновой части децимет­рового диапазона применяют тороидальные резонаторы с формой поперечного сечения, приведенной на рисунке 6. Для проектирования используют математические модели разного уровня.

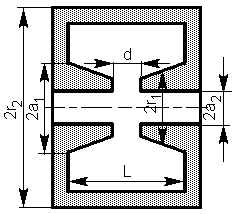
Рисунок 6 – Тороидальный резонатор.

Наиболее строгие модели высшего уровня основаны на системе уравнений Мак­свелла для электромагнитного поля, распределенного в объеме резонатора, и численных ме­тодах решения этих уравнений. Такие модели называются распределенными.

В данной ра­боте используются более простые (сосредоточенные) модели, основанные на представлении резонатора в виде эквивалентной схемы с сосредоточенными постоянными (рисунок 7).

Р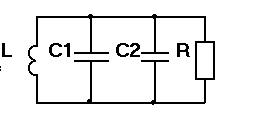 исунок 7 – Эквивалентная схема тороидального резонатора.

Харак­теристическое сопротивление, добротность и длина волны, определяются соотношениями:

ρ = 60 ∙ π ∙ L / λ₀ = 16,7 / π ∙ ( C1+C2 )

Q = R / ρ λ₀ = 5.95 √L ∙ ( C1-C2 )

При расчете резонатора мы решаем задачи параметрического синтеза и параметриче­ской оптимизации. В задаче синтеза мы добиваемся наиболее удобной конструктивной формы, а также возможно большее значение характеристического сопротивления. Задача параметрической оптимизации решается для выходного резонатора с целью получения мак­симальной полосы пропускания. При условии, что амплитуда переменного напряжения на зазоре выходного резонатора равна Uo/M, полоса пропускания определяется как:

∆f / f0 = I1 ∙ M 2 ∙ ρ ∙ G0 / I0

Где fo-резонансная частота; Ii- амплитуда первой гармоники конвекционного тока в сере­дине зазора; Iо - ток луча; М - усредненный по сечению потока коэффициент взаимодейст­вия; Go - проводимость луча; Uo - ускоряющее напряжение. Внутренними параметрами являются размеры резонатора a, d, r1, r2, h , из них управляемыми параметрами в данном случае являются два - ширина зазора взаимодействия d и высота резонатора h.

Длина зазора d и высота резонатора h выбираются из следующих соображений. Минимальная высота резонатора определяется шириной зазора, то есть hmin = d, а максимальная высота hmax ограничена расстоянием между центрами зазоров со­седних резонаторов. В клистронах оптимальная длина пролётных труб уменьшается от пер­вой к последней и самым коротким является расстояние Ln-1 между зазорами предпоследнего и выходного резонаторов. При одинаковой высоте резонаторов это расстояние с учётом толщины стенки определяет размер hmax.

Оптимальная длина последнего пролёта определяется из условия получения режима группирования, переходного от режима колебаний к режиму перегона. При этом на входе в зазор последнего резонатора образуется узкий сгусток без перегонов электронов с мини­мальным разбросом скоростей.

При выборе длины зазора d следует исходить из следующих соображений. При увели­чении величины d, с одной стороны, увеличивается характеристическое сопротивление за счёт уменьшения эквивалентной ёмкости, а с другой стороны, уменьшение М. Рекоменду­ется предварительно выбрать d в пределах (1...1,5)∙а, меньшие значения относятся к длинно­волновым клистронам, большие к коротковолновым. При изменении d в процессе проекти­рования необходимо следить за выполнением условия: N>0,7.

Внешние радиусы коллекторных труб r₁ и а₁ (рис.7) определяются из следующих конструктивных соображений. Конусные трубы применяют для уменьшения толщины торца труб  = r - a, и тем самым уменьшить торцевую емкость С₁. Но вместе с тем сохранить механическую прочность трубы и теплоотвод от торца.

Высота h изменяется от h_min до h_max. Минимальная высота резонатора определяется шириной зазора, h_min=d, а h_max ограничена расстоянием между центрами зазоров соседних резонаторов. В клистронах оптимальная длина пролетных труб уменьшается от первой к последней, и самым коротким является расстояние l_n-1 между зазорами предпоследнего и выходного резонаторов. При одинаковой высоте резонаторов это расстояние с учетом толщины стенки l_ст определяет размер h_max:

h_max=l_N-1-l_cт, (11)

где N – число резонаторов.

Оптимальная длина последнего пролёта l_N-1 определяется из условия получения режима группирования, переходного от режима нелинейных колебаний к режиму перегона. При этом на входе в зазор последнего резонатора образуется узкий сгусток без перегона электронов с минимальным разбросом скоростей и l_N-1 определяется соотношением.

где ₀=(2eU₀/m)^0.5 – постоянная составляющая скорости электронов,

- плазменная частота, F^1/2=f(a,b,U₀,₀) – коэффициент редукции плазменной частоты в линейном режиме.

В результате расчета определяются размеры h, d и r₂ (рис. 4.), соответствующие резонатору с максимальной полосой пропускания, а также параметры М, Q, R, .