1. Оптимальное рапределение грузовых потоков методов потенциалов

Классическая транспортная задача заключается в распределение грузопотоков между потребителями и поставщиками. В общем виде её можно представить как математическую модель:

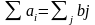
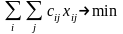
где i-количество поставщиков;

j-количество потребителей;

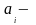общий объём груза у поставщиков;

-общий объём груза у потребителей;

-элементы целевой функции;

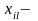объём перевозимого груза между пунктами поставщиков и потребителей

В качестве критерия оптимальности принимаем транспортную работу в тонно-километрах.

Рассмотрим задачу:

Даны грузообразующие пункты А1, А2, А3 и пункты грузополучателей Б1, Б2, Б3, а также количество вывозимого груза и количество ввозимого груза. Необходимого определить оптимальный план грузопотоков между потребителями и поставщиками. Исходные данные взять из таблицы 1 и таблицы 2.

Таблица 1

Исходные данные

№ варианта	Количество груза, т
	А1	А2	А3	Б1	Б2	Б3	Б4
13	10	40	30	30	20	10	20

Таблица 2

Исходные данные

№ вариант	Расстояние между вершинами, км
	А1-Б1	А1-Б2	А1-Б3	А1-Б4	А2-Б1	А2-Б2	А2-Б3	А2-Б4	А3-Б1	А3-Б2	А3-Б3	А3-Б4
13	4	8	6	4	2	8	6	4	9	3	7	1

Для решение задачи методом потенциалов составляется базисный план, который заносится в исходную матрицу. Он должен содержать m+n-1 загруженных клеток. Груз распределим с помощью способа северо-западного угла. Распределение груза по потребителям начинается с верхней левой клетки на пересечение строки А1 и графы Б1в таблице 1.Вывозим из А1 массу груза 10 тоны, требуемого Б1. Вывозим из А2 массу груза 20 тонн, требуемого Б2. Из А2 вывозим груз массой 20 тонн, требуемого Б2. К потребителю Б3 вывозим груз из А3 массой 20 тонн в клетку А3Б3.К потребителю Б4 вывозим оставшиеся 10 тонн . Клетки таблицы 1 в которых есть груз называются загруженными, а остальные свободными(потенциальными). Потенциал для первой строки таблицы береться равным нулю.

Таблица 1

Базисный план

	Б1	Б2	Б3	Б4	Итого по вывозу	Потенциал строк
А1	4 10	10 8	8 6	2 4	10	0
А2	2 20	8 20(-)	6 0 (+)	0 4	40	-2
А3	3 9	9 3 ×(+)	7 10(-)	1 20	30	-1
Итого по ввозу	30	20	10	20
Потенциал столбцов	4	10	8	2

Затем по расстояниям и загруженных клеток подбираются потенциалы для других строчек и столбцов таблицы так, чтобы расстояние каждой закруженной клетки равнялось сумме потенциалов строки и столбца, в которых находиться данная клетка:

где

Так, если для первой строки таблицы взят потенциал, равный нулю, то потенциал столбца Б1 будет равен 4, так как разность между расстояниями загруженной клетки А1Б1 и потенциалом первой строки равна 4(4 – 0 =4).

Потенциал первого столбца Б1 будет равен 4. Тогда потенциал строки А2 будет определяться по расстоянию загруженной клетки А2Б1 и найденному потенциалу столбца Б1 (2 – 4 = 4).

Потенциал столбца Б2 определяеться через расстояние загруженной клетки А2Б2 и найденный потенциал второй строки: 8 – ( - 2) =10.

Таким же образом находим потенциалы строки А3 и столбца Б4.

Если число загруженных клеток будет меньше, чем n + m – 1, то потенциалы для некоторых строк и столбцов невозможно определить. Чтобы устранить это вырождение, недостающее количество клеток загружают нулями. Клетки, загруженные нулями, рассматриваются как обычные загруженные клетки.

При полученном таким образом базисном плане транспортная работа составит:

Р= 10∙4+20∙2+20∙8+10∙7+20∙1=330 (т∙км)

Перераспределение груза в углах контура дает новый вариант решения задач (табл. 2), который не является оптимальным. Наиболее потенциальной будет клетка А2Б2.

Таблица 2