26.Зв'язок між моделями Мілі та Мура. Перехід від автомата Мура до автомата Мілі, та навпаки.

Як зазначалося, абстрактний автомат працює як перетворювач слів вхідного алфавіту в слова вихідного алфавіту.

Нехай абстрактний автомат Мілі заданий графомрис.1.5.

На вхід цього автомата, встановленого в початкова стан, надходить вхідний словоX=x₁, x₁, x₂, x₁, x₂, x₂.

Малюнок 1.5 - Граф автомата Мілі

Оскільки (a₁, x₁) = а₃, a (a₁, x₁) = y₁, то під впливом першої літери слова Х вхідного сигналу x₁автомат піде на стан a₃ і виході його з'явиться сигнал y_1. Далі, (а₃, x₁) = a₁, а (а₃, x₁) = у₂, тому після приходу другого сигналу x₁ автомат буде здатний a₁, але в виході його з'явиться сигнал у₂. Простеживши безпосередньо по графу чи таблицям переходів і виходів подальша поведінка автомата, опишемо його трьома рядками, перша у тому числі відповідає вхідному слову X, друга - послідовності станів, які проходить автомат під впливом літер слова X, третя - вихідному слову У, що з'являється не вдома автомата:

x₁ x₁ x₂ x₁ x₂ x₂

a₁ а₃ a₁ a₁ а₃ a₂ а₃

y₁ y₂ y₁ y₁ y₁ y₂

Назвемо у = (а₁, X) реакцією автомата Мілі може a₁ на вхідний слово X. Як очевидно з прикладу, у відповідь вхідний слово довжиниk автомат Мілі видає послідовність станів довжиник+1 і вихідний слово довжиниk. Загалом вигляді поведінка автомата Мілі, встановленого до стану а_>m, можна описати так:

>Входное слово	xі1	xі2	xі3
Послідовність станів	a>m	a>i2= (a>m,x>i1)	a>i3= (a>i2,x>i2).
>Виходное слово	yі1= (a>m,xі1)	y>i2= (a>i2,x>i2)	y>i3= (a>i3,x>i3)

Так само можна описати поведінка автомата Мура, що у стані a_>m, після приходу вхідного слова x_і1, x_>i2,., x_>ik. Нагадаємо, що згідно з (1-2) вихідний сигнал в автоматі Мура в останній момент часуt (У (>t)) залежить лише стану, де знаходиться автомат в останній моментt (a (>t)):

>Входное слово	xі1	xі2	xі3
Послідовність станів	a>m	a>i2= (a>m,x>i1)	a>i3= (a>i2,x>i2)	a>i4= (a>i3,x>i3)
>Виходное слово	yі1= (a>m,xі1)	y>i2= (a>i2,x>i2)	y>i3= (a>i3,x>i3)	yі4= (aі4)

Вочевидь, що вихідний сигнал у_>i1=> (a_>m) в останній момент часу і₁ залежить від вхідного сигналу x_і1, а визначається лише становищем а_>m.

Отже, цей сигнал y_і1 неможливо пов'язані з вхідним словом, що надходять на вхід автомата, починаючи з і₁. У зв'язку з цим під реакцією автомата Мура, встановленого до стану a_>m на вхідний словоX=x_і1, x_>i2,., x_>ik усвідомимо вихідний слово тієї самої довжини у= (a_>m, Х) =у_>i2, у_>i3,., y_>ik+1.

Як приклад розглянемо автомат МураS5, граф якого зображений нарис.1-6, і знайдемо його реакцію в початковому стані те що саме вхідний слово яку ми використовували під час аналізу поведінки автомата МіліS1:

>Входное слово	x1	x1	x2	x1	x2	x2
Послідовність станів	a1	a4	a1	a1	a4	a3	a5
>Виходное слово	y1	y1	y2	y1	y1	y1	y2

Малюнок 1-6 - Граф автомата Мура

Як очевидно з цього й попереднього прикладів, реакції автоматівS5 іS1 в початковому стані на вхідний слово Х з точністю до зсуву на 1 такт збігаються (реакція автомата Мура обведена лінією). Дамо тепер суворе визначення еквівалентності повністю певних автоматів.

Два автомата P.S_A і P.S_B з вхідними і вихідними алфавітами називаються еквівалентними, коли після встановлення в початкові стану їх реакцію будь-яке вхідний слово збігаються.

Переход от автомата Мили к автомату Мура и обратно Абстрактный автомат может работать, как некоторый преобразователь входного слова в слова выходного алфавита Пусть на вход этого автомата поступает входное слово –   (последовательность входных сигналов). Назовем переменную   реакцией автомата, находящегося в состоянии а₀, на входное слово  . Автомат Мили в ответ на входное слово длиной k выдает последовательность состояний длиной k+1 и выходное слово длиной k. Зададим автомат Мура. Найдем реакцию автомата Мура на входное слово –  . Начальное состояние x1: x1x4x2x1x4x3x5 Два автомата S_А и S_B с одинаковыми входным и выходным алфавитом называются - эквивалентными, если после установления их в начальное состояние реакции на любое входное слово совпадают. Можно показать, что для любого автомата Мили существует эквивалентный ему автомат Мура, и наоборот. При написании алгоритма взаимной трансформации часто пренебрегают выходным сигналом, связанным с начальным состоянием. Рассмотрим переход от автомата Мура к автомату Мили. Пусть задан автомат Мура: Необходимо построить автомат Мили, эквивалентный автомату Мура: Функцию   определим следующим образом: если в автомате Мура имеются функции  , то для автомата Мили можно записать следующую функцию выхода:  . 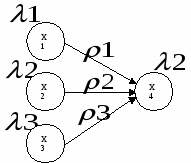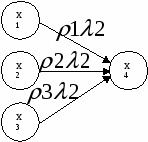Рассмотрим переход от автомата Мура к автомату Мили с помощью графа: Для осуществления перехода от автомата Мура к автомату Мили выходной сигнал  , находящийся в автомате Мура рядом с вершиной, для автомата Мили передается на все дуги, входящие в эту вершину.  ^ Переход от автомата Мура к Мили табличным способом: Поскольку таблица переходов автомата Мура полностью совпадает с таблицей переходов автомата Мили, то основная проблема при описании автомата Мили табличным способом – это составление таблицы выходов. Таблица выходов автомата Мили получается из таблицы переходов автомата Мура путем замены символа соответствующего внутреннему состоянию автомата Мура символом выходного сигнала. Для автомата Мура

		1	2	3
1	X1	X1	X2	X4
2	X2	X2	X3	X1
1	X3	X1	X3	X4
3	X4	X1	X1	X4

Для автомата Мили

	1	2	3
X1	1	2	3
X2	2	1	1
X3	1	1	3
X4	1	1	3

Из самого способа построения автомата Мили очевидно, что он эквивалентен автомату Мура. 

Для входной последовательности ^ Ф поведение автоматов S_а и полностью совпадают. По индукции не трудно доказать, что любое входное слово конечной длины, поданное на входы автоматов S_а и S_В, установленных в начальное состояние x₀ вызовет появление одинаковых выходных слов. 
Переход от автомата Мили к автомату Мура. При переходе от автомата Мили к автомату Мура необходимо наложить следующие ограничения: в автомате Мили не должно быть преходящих состояний.

Преходящее состояние - это состояние, в которое при представлении автомата в виде графа не входит ни одна дуга и которое имеет хотя бы одну выходящую дугу.

Задан автомат Мили S_а . Необходимо построить автомат Мура S_В. 

Алфавиты должны совпадать:





Для определения множества X_B каждому состоянию   поставим соответствующее множество пар вида  ,где   -это выходной сигнал приписанный дуге, входящей в x_s.







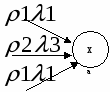
Число элементов в множестве X_S будет равно числу различных выходных сигналов на дугах автомата Мили S_A, входящих в состояние x_aЧисло внутренних состояний автомата Мура будет определяться объединением множеств всех X_S.



X_A => X_B 

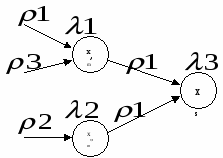
Функция переходов   и функция выходов   определяется так: если в автомате Мили имеется переход из состояния x_m в состояние x_s под воздействием   



и при этом выдается выходной сигнал 

,

то в автомате Мура будет переход из множества состояний X’_m, порождаемое внутренним состоянием x_m под воздействием входного сигнала  . 

.

Функция выходов автомата Мура определяется следующим образом



В качестве начального состояния x_0B можно взять любое состояние из множества, которое порождается начальным состоянием x_0А.

Т. о. получается автомат S_В, эквивалентный автомату S_A.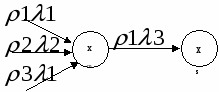




Автомат Мили Автомат Мура
Изложенные методы взаимных транспозиций модели Мили и Мура показывают, что при переходе от автомата Мура к Мили число состояний автомата не меняется, а при обратном переходе число состояний, как правило, возрастает.

Вследствие транзитивности отношения эквивалентности  . Два автомата Мили также будут эквивалентны, хотя у последнего на два состояния больше. Таким образом, эквивалентные автоматы могут иметь различное число внутренних состояний. В связи с этим возникла задача нахождения минимального автомата в классе эквивалентных между собой автоматов.