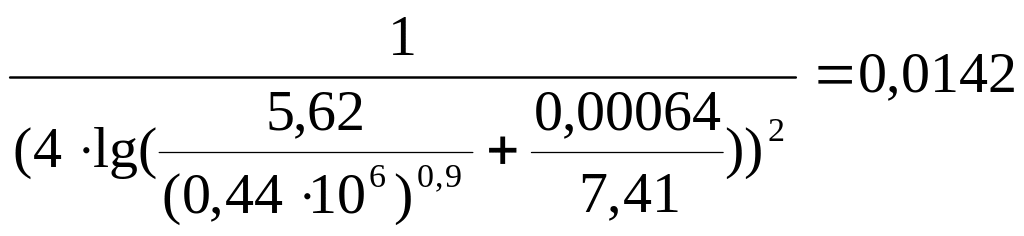6.3. Визначення середнього значення температури та тиску в газопроводі.

Середня температура газу на ділянці трубопроводу може бути визначена на основі залежності Шухова:

= Т– (Т–Т) · (3.1)

де, Т– зведена температура навколишнього середовища (К);

Т– температура газу на початку ділянки газопроводу (К);

Залежність Шухова з урахуванням Джоуля‑Томсона може бути записана у вигляді:

Т= Т‑ D· (3.2)

де, Т= 0°С = 273 К – температура ґрунту в непорушеному стані;

D– коефіцієнт дросель‑ефекту Джоуля‑Томсона;

p– середній тиск на ділянці газопроводу;

а – коефіцієнт, який враховує втрату тепла газу з трубопроводу до навколишнього середовища.

= · (3.3)

Значення коефіцієнту а знаходимо за наступною формулою:

а = (3.4)

де, k– повний коефіцієнт теплопередачі від газу до навколишнього середовища, (ккал/м· год · град);

C– ізобарна теплоємність газу (ккла/кг·°С);

Q – оптимальний дебіт свердловини (м/добу)

Згідно завдання:

p= P=5,9 МПа;

p= P= 5,0 МПа;

L = l= 2,1 км

Середній тиск в газопроводі буде дорівнювати:

= · = = 4,22 МПа

Середня температура в газопроводі дорівнює:

= (3.5)

Згідно завдання:

Т= Т= 295 K;

Т= Т= 277 K.

Звідси:

= = = 310,3 K

6.3.1. Визначення коефіцієнту надстисливості газу.

Коефіцієнт надстисливості газу при середніх значеннях тиску і температури може бути знайдений за номограмою II.8 але спочатку за номограмами II.2а та II.2б знаходимо критичні тиски та температури для середніх значень ,, які залежать від відносної густини газу за повітрям , а потім їх приведенні значення.

Приведений тиск визначається за формулою:

p= (3.6)

Приведена температура визначається за формулою:

Т= (3.7)

За номограмою II.2а для газу з =0,7; p= 4,73 МПа.

За номограмою II.2б для газу з =0,7; T= 217 K.

Звідси:

p= = =0,89;

Т= = =1,43.

Відповідно за номограмою II.8 коефіцієнт надстисливості газу, визначений для середніх значень тиску та температури =0,877.

6.3.2. Визначення коефіцієнту гідравлічного опору газопроводу.

Коефіцієнт гідравлічного опору газопроводу λ залежить від режиму руху газу на поверхні стінок труб. При швидкостях потоку газу, які зустрічаються на практиці, основними параметрами від яких залежить λ є число Рейнольдса R та відносна шорсткість труб ε, які можна визначити за наступними формулами:

R= k · (3.8)

ε = (3.9)

де, l– еквівалентна шорсткість, яка дорівнює приблизно l= 0,03 мм;

μ – абсолютна (динамічна) в’язкість, яка може бути визначена за номограмою 11.4 в залежності від значень відносної густини газу за повітрям та середньої температури , (сП);

Q – оптимальний дебіт свердловини, (тис.м/добу);

d – внутрішній діаметр газопроводу, см;

k – розмірний коефіцієнт, який при стандартних умовах (20°С та 760 мм.рт.ст.) k = 1777, а при 0°С та 760 мм.рт.ст. ­ k = 1910

Коефіцієнт гідравлічного опору газопроводу λ при ламінарному русі не залежить від шорсткості труб і дорівнює:

λ = (3.10)

Коефіцієнт гідравлічного опору газопроводу λ при турбулентному русі є функцією Rта ε і дорівнює:

λ = (3.11)

Також коефіцієнт гідравлічного опору газопроводу λ при турбулентному русі можна визначити за номограмою III.1, яка побудована за формулою (3.12).

При великих витратах наступає так звана турбулентна автомодельність, коли λ не залежить від Rі визначається за формулою:

λ = (3.12)

Згідно завдання:

d = D– 2 · δ= 114 – 2 · 10 = 94 мм = 9,4 см

Відповідно номограмі II.4 при =0,7; = 310,3 = 37,3ºC абсолютна в’язкість μ = 0,01044 МПа · с = 0,01044 · 10Па · с = 0,01044 · 10П = 0,009 сП.

При Q = 30 тис.м/добу та d = D– 2 · δ= 114 – 2 · 10 = 94 мм = 9,4 см число Рейнольдса буде дорівнювати:

R= k · = = 441099,27 = 0,44 · 10

ε = = = 0,00064

Маємо випадок турбулентного руху.

λ = =