11. Главные линии плоскости (горизонталь, фронталь, линия ската).

• Горизонталь - линия уровня, параллельна плоскости П1. Все горизонтальные плоскости и их горизонтальные проекции параллельны между собой и параллельны горизонтальному следу этой плоскости.

• Фронталь - линия уровня, параллельна плоскости П2. Все фронтальные плоскости и их фронтальные проекции параллельны между собой и параллельны фронтальному следу этой плоскости.

• Линия ската – линия наибольшего наклона к горизонтальной плоскости проекции, линия принадлежащая плоскости и перпендикулярная горизонтальному следу.

12. Взаимное положение точек прямых и плоскостей.

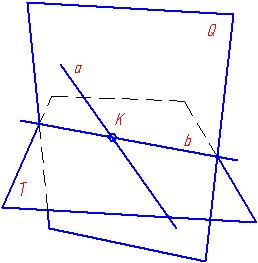
• Определение взаимного положения прямой и плоскости - позиционная задача, для решения которой применяется метод вспомогательных секущих плоскостей. Сущность метода заключается в следующем: через прямую проведем вспомогательную секущую плоскость Q и установим относительное положение двух прямых a и b, последняя из которых является линией пересечения вспомогательной секущей плоскости Q и данной плоскости T.

Метод вспомогательных секущих плоскостей

13. Поверхности, понятия и определения (каркас, очерк, определитель). Классификация поверхностей.

• Поверхность – это двухпараметрическое множество точек или однопараметрическое множество линий.

• Поверхность образованная перемещением в пространстве некоторой линии называется кинематической.

• Непрерывная последовательность образующих и направляющих образуют каркас поверхности.

• Каркасом поверхности принято называть упорядоченное множество точек или линий, принадлежащих поверхности.

• Определителем поверхности называют совокупность независимых условий, однозначно определяющих данную поверхность. Определитель состоит из двух частей:

• Геометрический (оси, образующие);

• Алгоритмический – закон формирования поверхности.

• Очерк - это проекция контура на плоскости проекции.

• Очерком поверхности называется след цилиндрической проецирующей поверхности, со всех сторон огибающей данную поверхность на плоскости проекции.

• Классификация поверхностей

а)линейчатые поверхности, образуемые движением прямой линии, в частности, винтовые поверхности, образуемые, движением прямой линии по винтовым направляющим б) поверхности вращения, образуемые вращением произвольной образующей вокруг неподвижной оси в)циклические поверхности, образуемые движением окружности г)поверхности второго порядка д) топографические поверхности, которые не могут быть образованы по какому-либо простому закону и задаются на чертеже семейством некоторых линий по шаблонам

14. Линейчатые поверхности(развертываемые):коническая, цилиндрическая, торсовая.

• Линейчатая поверхность образована движением образующей l по направляющей m и постоянно проходящей через точку называется конической

• линейчатая поверхность образована движением образующей l, проходящей через несобственную точку и пересекающей направляющую кривой m, называется цилиндрической.

• Торсовой называется поверхность, образованная прямолинейной образующей l , касающейся при своем движении во всех своих положениях некоторой пространственной кривой т, называемой ребром возврата. Ребро возврата полностью задает торс и является геометрической частью определителя поверхности. Алгоритмической частью служит указание касательности образующих к ребру возврата.

15. Поверхности вращения.

• Поверхностью вращения называют поверхность, образованную вращением какой-либо линии m – образующей – вокруг некоторой прямой i, называемой осью вращения (осью поверхности).

16. Винтовые поверхности.

• Винтовой называется поверхность, которая описывается какой-либо линией (образующей) при ее винтовом движении.  Винтовое движение линии характеризуется ее вращением вокруг определенной оси i и поступательным перемещением, параллельным оси i.

17. Поверхности параллельного переноса.

• Поверхностью параллельного переноса называется поверхность, образованная поступательным плоскопараллельным перемещением образующей - плоской кривой линии  m по криволинейной направляющей n

18. Методы преобразования комплексного чертежа, как основа решения метрических задач. Способ замены проекций.

• Способами преобразования комплексного чертежа могут быть решены только те метрические задачи, которые имеют только один геометрический элемент, несущий на себе одну искомую численную характеристику. Алгоритм решения метрической задачи с помощью преобразования комплексного чертежа сводится к следующему: 1) определяется геометрический элемент оригинала, несущий на себе искомую численную характеристику и, 2) определяется “решающее положение” оригинала по отношению к плоскости проекций. (Решающим положением оригинала называют такое положение, при котором геометрический элемент, несущий на себе искомую численную характеристику, может быть спроецирован на плоскость проекций без искажений). Решающих положений может быть только четыре, и им соответствуют и четыре известных задачи на преобразование комплексного чертежа.

19. Позиционные задачи. Алгоритм решения задач на взаимное пересечение геометрических образов: пересечение прямой с плоскостью; пересечение двух плоскостей; пересечение поверхностей (многогранника, цилиндра, конуса, сферы) с плоскостью; пересечение двух поверхностей: способ параллельных секущих плоскостей.

• Задачи, связанные с решением взаимного расположения геометрических фигур на комплексном чертеже, называются позиционными.

• Пересечение прямой с плоскостью.

Если прямая не лежит в плоскости и не параллельна ей, она пересекает плоскость. Задача на определение точки пересечения прямой с плоскостью сводится к следующему: 1) проведению вспомогательной плоскости (Вспомогательную плоскость рекомендуется выбирать такую, которая даст наиболее простое графическое решение задачи) через данную прямую; 2) нахождению линии пересечения вспомогательной плоскости с данной плоскостью; 3) определению точки пересечения данной прямой с линией пересечения плоскостей, а следовательно, с данной плоскостью.

• Чтобы построить линию пересечения двух плоскостей, достаточно найти точки пересечения любых двух прямых, принадлежащих первой плоскости, со второй плоскостью

• Построение линии сечения поверхности плоскостью сводится к построению точек пересечения отдельных линий поверхности с данной плоскостью Алгоритм построения линии сечения:  1. Исходя из формы поверхности подбирают вспомогательные плоскости,  которые как посредники несут на себе образующие данной поверхности и линии данной плоскости. 2. Строят линии пересечения этих посредников с данной поверхностью и плоскостью в отдельности.  3. Определяют точки пересечения полученных на посредниках вспомогательных линий сечения. Эти точки принадлежат искомой линии сечения. Точки последовательно соединяют между собой, учитывая видимость.

• Для решения задачи на пересечение поверхностей, занимающих произвольное положение относительно плоскостей проекции их необходимо предварительно перевести в частное положение средствами преобразования чертежа.