Раздел: «Начертательная геометрия»

1. Предмет «начертательная геометрия»

• НГ это наука, изучающая методы отображения пространства на плоскость и способы графического решения стереометрических задач. НГ является геометрической базой конструкторского творчества, азбукой, необходимой для создания чертежей.

2. Ортогональные проекции. Эпюр Монжа. Метод координат. Комплексный чертеж точки(названия и обозначения основных плоскостей проекции). Постоянная Монжа. Приемы построения третьей проекции точки.

• при центральном проецировании луч проходит через точку А и центральную точку до пересечения с плоскостью проекции, точка пересечения луча и плоскости - центральная проекция точки А на плоскость

• при параллельном проецировании проецирующий луч проходит через объект(точку В) в некотором направлении S до пересечения с плоскостью , полученная точка B_i параллельная(косоугольная) проекция точки В на плоскость

• частным случаем параллельного проецирования является ортогональное проецирование(прямоугольное).Когда проецирующий луч проходит перпендикулярно плоскости.

Основные свойства ортогонального проецирования:

• проекция точки есть точка

• проекция линии в общем случае (частный случай прямая) есть линия

• проекция плоскость (поверхности) есть плоскость (поверхность)

• если в пространстве точка принадлежит линии, то ее проекция будет принадлежать этой линии

• проекции параллельных прямых параллельны

• если точка в пространстве делит проекцию в каком-либо соотношении, то и проекция точки будет делить в таком же соотношении

• любая плоская фигура, расположенная в плоскости параллельно поверхности проецируется в плоскость в натуральную величину

• любая плоская фигура, расположенная в плоскости, проецируется в отрезок прямой

• при ортогональном проецировании проекция отрезка будет меньше или равна самому отрезку

• (теорема прямого угла) прямой угол проецируется в прямой без искажения, если одна сторона прямого угла параллельна плоскости поверхности, а другая не перпендикулярна

Компл.чертеж (эпюр монжа)

• Чертеж называется обратимым, если по изображению геометрического тела на плоскости можно определить его форму, размер и положение в пространстве(множество точек пространства – трехпараметричны, мн. Точек плоскости – двухпараметричны, мн. Точек линий - однопараметричны). Для получения обратимого чертежа можно предложить проецировать геометрическое тело на 2 или 3 взаимно перпендикулярные плоскости с последующим совмещением в одну плоскость. Плоскость П2 принимают за неподвижную плоскость, П1 и П2 вращаем вокруг х и у до совмещения с П2.

• П1 – горизонтальная плоскость

• П2 – фронтальная плоскость

• П3 – профильная плоскость

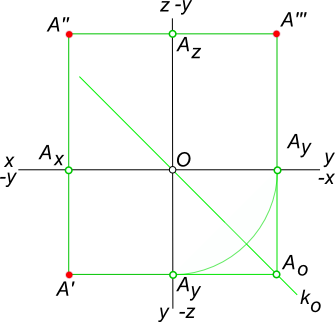
• Биссектриса ОА₀ – постоянная прямая эпюра Монжа – k₀

3 Линии. Прямая, задание на чертеже. Прямая общего положения(комплексный чертеж, обозначения). Следы прямой.

• Частный случай линии – прямая. Так как прямая в пространстве определена двумя точками, то чертеж прямой можно построить построив чертежи двух ее точек. Прямая, расположенная под углом к плоскостям проекции называется прямой общего положения.

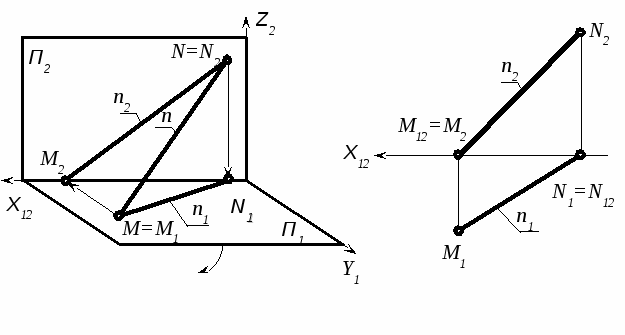
• Точка пересечения прямой с плоскостью называется следом прямой.