Построение циклического кода по методу деления на образующий полином. Пример кодирования.
Циклические коды
Циклические коды или CRC-коды (cyclical redundancy check – избыточные коды с циклическими проверками) были получены в поисках более простой технической реализации помехоустойчивого кодирования.
Благодаря хорошим корректирующим свойствам, относительно малой избыточности, простоте схемной реализации устройств кодирования и декодирования CRC–коды получили широкое распространение.
Основным свойством
CRC–кодов
является то, что все полиномы
,
представляющие кодовые комбинации
CRC–кода
(разрешенные комбинации), делятся без
остатка на полином
степени m,
который называется образующим
или производящим
полиномом.
Кодирование
Под кодированием понимается преобразование безызбыточной k– разрядной комбинации в n=k+m–разрядную комбинацию CRC–кода.
На практике широко используется кодирование по методу деления на образующий полином, согласно которому выполняется следующие операции:
Подлежащая кодированию безызбыточная k–разрядная кодовая комбинация описывается полиномом Ck (x) степени (k-1).
Полином Ck(x) умножается на xm, что эквивалентно сдвигу безызбыточной k-разрядной комбинации влево (в сторону старших разрядов), на m разрядов или добавлению m нулей справа.
Полученный полином Ck(x)xm делится на образующий полином Gm(x), имеющий степень, равную числу проверочных символов m, в результате чего получается целая часть Q(x) и остаток деления R(x):
,
(*)
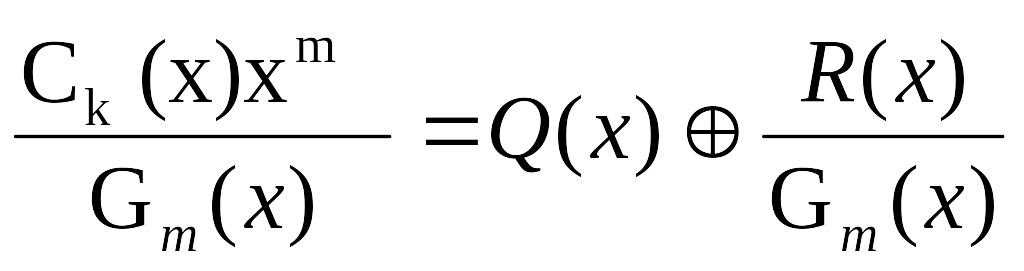где – знак суммирования по модулю два.
Формируется n – разрядная разрешенная комбинация CRC–кода, соответствующая полиному:
,
для чего в освободившиеся при сдвиге разряды записывается комбинация, соответствующая остатку R(x).
Покажем, что комбинации,
соответствующие полиному
,
являются разрешенными.
Умножим обе части уравнения (*) на Gm(x):
.
Вычитая из обеих частей R(x) и учитывая, что операция вычитания и суммирования по mod2 эквивалентны, получим:
.
Выражение в левой части этого равенства - это полином . Следовательно
- целая часть,
т.е. полученный полином делится на Gm(x) без остатка, а значит - представляет разрешенную комбинацию циклического кода (на основании основного свойства циклического кода).
Пример1. Построим кодовую комбинацию CRC–кода (7,4), соответствующую безызбыточной комбинации 1001.
Общая длина комбинации
n=7,
число информационных символов k=4,
проверочных – m=n–k
= 3. Из таблицы неприводимых полиномов
табл. 1.1 для m=3
выберем образующий полином
.
В соответствии с рассмотренным методом
кодирования получаем:
1.
2.
3.
4.
Все указанные операции можно выполнять непосредственно над кодовыми комбинациями.
Пример 2:
1001
1001000
4. 1001 110