12. Помехоустойчивое кодирование. Понятие избыточности кода. Коэффициент избыточности. Принцип обнаружения ошибок в кодах с избыточностью.

Помехоустойчивое кодирование

Помехоустойчивые коды – это коды, способные обнаруживать, исправлять или обнаруживать и исправлять ошибки. Эту способность они приобретают за счет избыточности, которую можно понимать в том смысле, что в комбинации этих кодов вводятся дополнительные (избыточные) символы.

Т.о. помехоустойчивые коды – это коды с избыточностью.

Избыточность кода оценивают коэффициентом избыточности , которые определяется следующим образом:

.

Здесь

n – число разрядов в комбинации кода с избыточностью, с помощью которого можно закодировать M сообщений,

k - число разрядов в комбинации кода без избыточности, с помощью которого можно закодировать те же M сообщений, причем для двоичных кодов (кодов с основанием 2)

,

где ][ - операция округления до ближайшего большего целого.

Например, если код используется для передачи M=10 сообщений и его комбинации имеют n=8 разрядов, то

и .

В основу помехоустойчивого кодирования положена следующая идея.

Пусть из набора элементарных (в частности двоичных символов) можно составить N двоичных кодовых комбинаций. При этом только N₀ используются для передачи – они называются разрешенным. Остальные N-N₀ комбинаций не используются для передачи сообщений - они называются запрещенными. Эту идею часто иллюстрируют с помощью множества точек на плоскости (рис.1), каждая из которых рассматривается как модель соответствующей кодовой комбинации.

Рис.1 (+ - разрешенные комбинации, * - запрещенные комбинации)

При этом появляется возможность обнаруживать ошибки.

Принцип обнаружения ошибок

Принцип обнаружения ошибок состоит в следующем.

Получателю известно множество разрешенных и множество запрещенных комбинаций. Пусть передается разрешенная комбинация, но под действием действующих в канале искажений она изменяется, т. е. переходит в запрещенную. Поскольку получатель знает, что такая комбинация не может передана, то ошибка обнаруживается. Если же одна разрешенная комбинация переходит в другую разрешенную, то такая ошибка не обнаруживается. Т.о., не все ошибки обнаруживаются избыточными кодами – они имеют ограниченную возможность по обнаружению и коррекции ошибок.

Иначе помехоустойчивый код можно рассматривать как код, в котором используются не все возможные кодовые комбинации, которые можно получить из элементарных (двоичных) символов. Рассмотрим это на следующем примере.

Пример.

Пусть для передачи сообщений используются комбинации 3-х-разрядного безызбыточного кода с четным числом единиц и нулевая комбинация (рис.2). Такой код называется кодом с проверкой на четность.

Запрещенные комбинации

Рис.2

Как следует из рис.3., ошибка в любом одном разряда передаваемой разрешенной комбинации (например, 011) приводит к запрещенной комбинации, а значит обнаруживается. Двухкратная ошибка (искажение двух любых разрядов) приводит к другой разрешенной комбинации, а значит не обнаруживается.

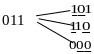
Рис.3

12. Понятие кодового расстояния. Минимальное кодовое расстояние. Геометрическая интерпретация кодового расстояния. Связь кратности обнаруживаемых и исправляемых кодом ошибок с минимальным кодовым расстоянием.

Кодовое расстояние

Для определения степени отличия одной комбинации от другой вводят в рассмотрение понятие кодового расстояния.

Кодовое расстояние указывает число разрядов, в котором одна кодовая комбинация от другой и может быть определено как число единиц в сумме по модулю два сравниваемых кодовых комбинаций.

Например, для комбинаций 0101101 и 1000111 кодовое расстояние d=4 в соответствии с числом единиц в сумме по модулю два этих комбинаций:

0101101

1000111

1101010

Минимальное кодовое расстояние

Важнейшей характеристикой помехоустойчивых кодов является минимальное кодовое расстояние или расстояние Хэмминга, которое определяется как минимальное кодовое расстояние между комбинациями кода:

Нетрудно проверить, что для рассмотренного кода с проверкой на четность , а для безызбыточного кода , т.е. всегда найдется две комбинации отличающиеся только в одном разряде.

Геометрическая интерпретация кодового расстояния

Геометрической моделью n-разрядного безызбыточного двоичного кода являются вершины n-мерного куба с единичными ребрами. Так, например для трехразрядного (n=3) кода С₁С₂С₃ имеем следующую модель (рис.4).

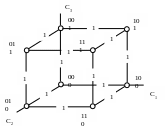
Рис.4

Геометрическая модель позволяет интерпретировать кодовое расстояние как минимальную сумму длин ребер, соединяющих вершины куба, координаты которых представляют кодовые комбинации.

Нетрудно видеть, что минимальное расстояние между вершинами куба равно 1, т.е. минимальное кодово расстояние для безызбыточного кода равно d=1.

Геометрическая модель 3-х-разрядного кода с проверкой на четность представлена на рис.5, где темные точки – запрещенные (неиспользуемые комбинации), а светлые - разрешенные. Очевидно, что минимальное расстояние между разрешенными комбинациями равно двум. т.е. минимальное кодовое расстояние для этого кода d_min=2.

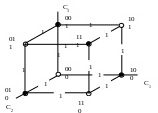
Рис.5

Связь кратности обнаруживаемых и исправляемых кодом ошибок с минимальным кодовым расстоянием

По минимальному кодовому расстоянию можно определить кратность (число ошибок в кодовой комбинации) обнаруживаемых, исправляемых и одновременно обнаруживаемых и исправляемых ошибок.

Кратность обнаруживаемых ошибок определяется по формуле

.

Кратность исправляемых ошибок определяется по формуле

.

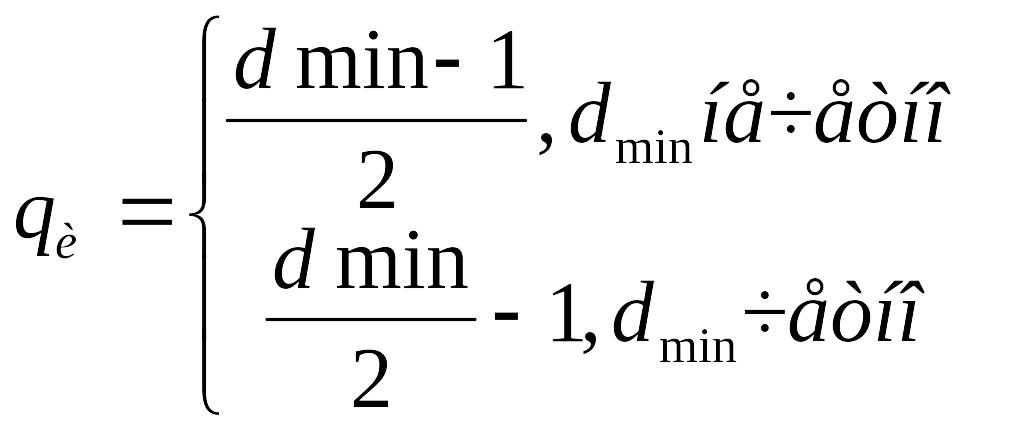Кратность обнаруживаемых и исправляемых ошибок определяется из соотношения

.

Классификация помехоустойчивых кодов

Помехоустойчивыми или корректирующими называются коды, способные обнаруживать и исправлять ошибки. Эту способность они приобретают за счет избыточности.

Дадим общую классификацию корректирующих кодов.

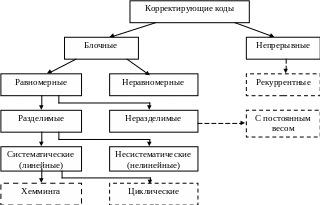
Корректирующие коды делятся на блочные и непрерывные. К блочным относятся коды, в которых каждому сообщению соответствует кодовая комбинация (блок) из двоичных символов. Эти комбинации кодируются и декодируются независимо. Если все комбинации имеют одинаковую длину, блочный код называется равномерным. В противном случае код неравномерный.

Равномерные блочные коды делятся на разделимые и неразделимые. В разделимых кодах можно выделить информационные и проверочные (избыточные) символы, которые занимают одни и те же позиции. В неразделимых кодах деление на информационные и проверочные символы отсутствует. К таким кодам относится код с постоянным весом (код на сочетания).

Разделимые коды в свою очередь делятся на систематические (линейные) и несистематические (нелинейные). В систематических кодах проверочные символы получаются путем нелинейного преобразования информационных символов. Кроме того, любую разрешенную комбинацию систематического кода, можно получить линейным преобразованием двух (или более) других разрешенных комбинаций. Нелинейные коды этими свойствами не обладают.

Представителями систематических кодов являются циклические коды и коды Хемминга.

Непрерывные коды, к которым относятся рекуррентные коды представляют собой непрерывную последовательность символов, ее разделение на блоки в процессе кодирования и декодирования не происходит. В таких кодах избыточные символы размещается в определенном порядке между информационными.