Топологические матрицы графов

Геометрия любого графа может быть описана несколькими матрицами. При расчетах наиболее часто используют следующие названия матриц: матрицу соединений (узловая матрица), контурную матрицу, матрицу главных сечений, матрицы параметров ветвей.

Узловая матрица (А). Рассмотрим направленный граф электрической цепи. Составим и заполним таблицу согласно правилам: - если ветвь графа направлена от узла, то в клетку пересечения их нумераций вписывается +1; - если ветвь графа направлена к узлу, то в клетку пересечения их нумераций вписывается −1; - если ветвь графа не связана с узлом, то в клетку пересечения их нумераций вписывается 0.

Таблица

У з л ы	В е т в и
	1	2	3	4	5	6
1	+1	0	0	+1	0	−1
2	−1	+1	0	0	+1	0
3	0	−1	−1	0	0	+1
4	0	0	+1	−1	−1	0

Согласно заполненной таблице запишем полную узловую матрицу:

А_П = , А = .

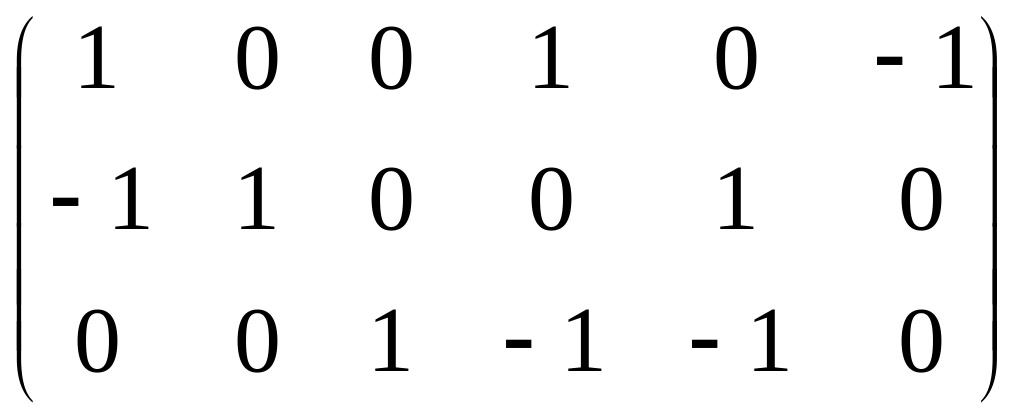которая и определяет схему электрической цепи.

Из матрицы А_П следует, что сумма чисел в любом столбце равна нулю, поэтому одна из ее строк является зависимой. В этом случае матрицу А_П заменяют матрицей А путем вычеркивания любой строки из матрицы А_П. Узел, из которого исключается строка, принято называть базисным. У графа такой узел обозначается через ноль. Тогда размер матрицы А равен . В нашем случае размер матрицы А будет: .

Перестановка столбцов или строк изменит лишь нумерацию ветвей и узлов, но не изменит схему цепи.

Составим соответствующую таблицу:

Контуры	В е т в и
	1	2	3	4	5	6
I	+1	0	0	−1	+1	0
II	0	+1	−1	0	−1	0
III	0	0	+1	+1	0	+1

Согласно заполненной таблице запишем матрицу главных контуров (контурная матрица):

В = .

Размер контурной матрицы В: .

Таблица

Главное сечение	В е т в и
	1	2	3	4	5	6
I	+1	0	0	+1	0	−1
II	0	+1	+1	0	0	−1
V	0	0	−1	+1	+1	0

Согласно заполненной таблице запишем матрицу главных сечений:

Q = .

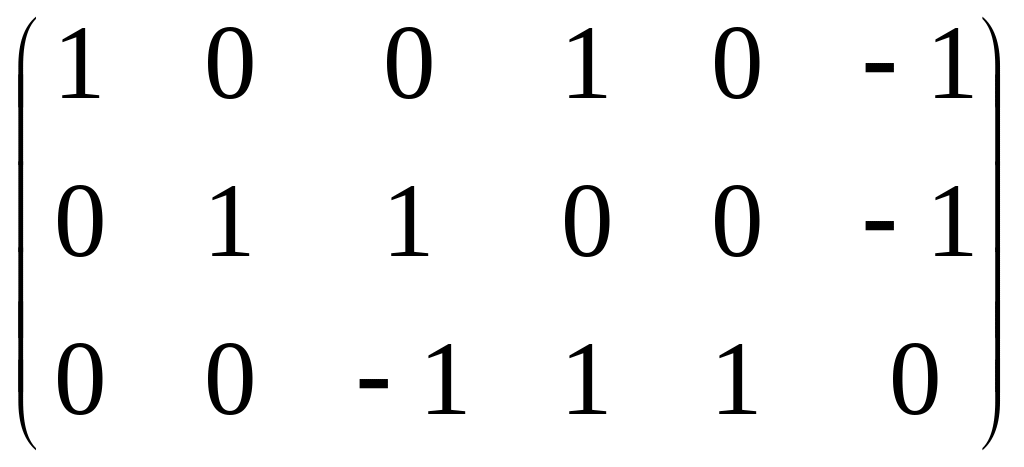Размер матрицы главных сечений Q: .

Для заданного графа организуем контурную матрицу:

В = .

Матрица сопротивлений ветвей будет диагональной размером :

Z_B = .

Далее находим произведение матрицы Z_B и транспонированной (когда строки и столбцы меняются местами) контурной матрицы В^Т:

Z_BB^T = ∙ = .

Матрицу контурных сопротивлений определит тройное матричное произведение:

Z_K = B Z_BB^T = ∙ =

= .

Матрица проводимостей ветвей (Y_B) - эта матрица будет так же диагональной, но обратной относительно матрицы сопротивлений:

Y_B = .

Матрицу узловых проводимостей определит тройное матричное произведение:

Y_q = AY_BA^T .

Матрицы источников ЭДС (Е) и токов (J) - это столбцовые матрицы, число строк в которых равно числу ветвей графа:

; .