Метод эквивалентного источника напряжения (теорема Гельмгольца-Тевенена)
Метод основан на теореме об эквивалентном источнике, когда активный двухполюсник по отношению к рассматриваемой ветви может быть заменен эквивалентным источником напряжения, ЭДС которого равна напряжению холостого хода на зажимах этой ветви, а его внутреннее сопротивление равно входному сопротивлению двухполюсника.
Рассмотрим электрическую цепь.
Решение
Ищем ток I1.
Представим исходную схему в следующем виде:
Для выделенной структуры составим уравнение по методу контурных токов и найдем ток I3:
Теперь можем найти напряжение холостого хода между зажимами А и В:
В.
Входное сопротивление к зажимам А, В найдем согласно схеме:
Ом.
Находим ток I1:
A.
Ищем ток I3.
Представим исходную схему в виде:
Для данной схемы уравнение по методу контурных токов будет иметь вид:
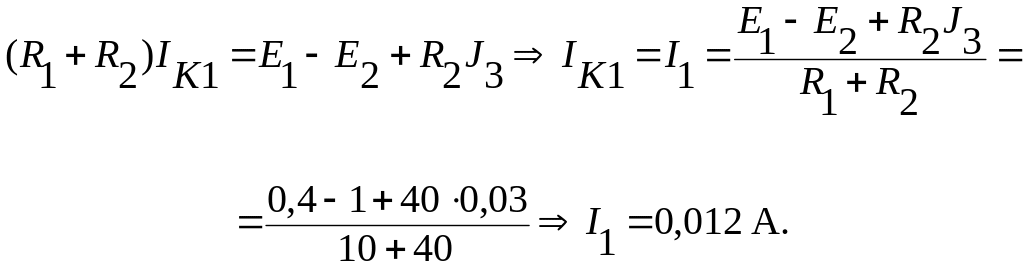
Тогда
В.
Входное сопротивление к зажимам А, В найдем согласно схеме:
Ом.
Находим ток I3:
А.
Рассмотрим электрическую цепь, в которой активный двухполюсник подключен к ветви с последовательно включенными сопротивлениями и амперметром.
Из опыта известны два показания амперметра: тока IA1, когда оба ключа разомкнуты и тока IA2, когда ключ K1 замкнут, а ключ K2 разомкнут.
Требуется вычислить показания амперметра при разомкнутом ключе K1 и замкнутом ключе K2 (см. рисунок).
Составляем уравнения для всех трех режимов:
1.
;
2.
;
3.
,
где
- напряжение
холостого хода на зажимах исследуемой
ветви.
Тогда
из первого уравнения
.
Из второго уравнения находим входное сопротивление двухполюсника.
;
После чего находим ток IА3.
Метод эквивалентного источника тока (теорема Нортона)
Активный двухполюсник по отношению к рассматриваемой ветви можно заменить эквивалентным источником тока, ток которого равен току в этой ветви, замкнутой накоротко, а внутренняя проводимость источника равна входной проводимости двухполюсника.
Применим этот метод к выше рассмотренной электрической цепи.
Требуется найти ток I1 и ток I3.
Ищем ток I1.
Представим схему в следующем виде:
Из схемы следует:
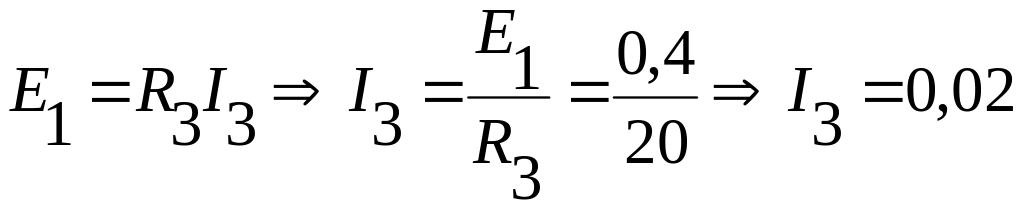А;
А.
Ток короткого замыкания JKЗ1 найдем из первого закона Кирхгофа:
А.
Входную проводимость к зажимам А, В найдем согласно схеме:
.
Находим ток I1.
А.
Ищем ток I3.
В этом случае схема приобретает вид:
Согласно схеме находим токи I1, I2:
А;
А.
Ток короткого замыкания JKЗ3 найдем из первого закона Кирхгофа:
А.
Входную проводимость к зажимам А, В найдем согласно схеме:
.
Находим ток I3.
А.
Потенциальная диаграмма.
Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат откладывают потенциалы. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме.
Потенциальная диаграмма строится, когда все токи и напряжения в цепи рассчитаны.
R
Отношение напряжения к сопротивлению рассматриваемого участка цепи будет соответствовать тангенсу угла наклона прямых, определяющих изменение потенциала, к оси абсцисс. Но поскольку ток в данной схеме остается неизменным, то и наклон прямых одинаков.