Трансформатор без стального сердечника

Широкое применение в электротехнике имеет трансформатор – устройство, предназначенное для преобразования величины переменных напряжений и токов. В простейшем случае он не имеет ферромагнитного сердечника и представляет собой две катушки с индуктивной связью.

Напряжение источника приложено к первичной катушке трансформатора, к вторичной катушке подключена нагрузка. Тогда уравнения по второму закону Кирхгофа для первичной и вторичной цепей при показанных на рисунке одноименных зажимах и положительных направлениях токов, при которых потоки самоиндукции и взаимоиндукции складываются, получают следующий вид:

,

где – напряжение на приемнике, и – сопротивление и индуктивность первичной и вторичной, катушек, соответственно.

При сопротивлении нагрузки уравнения трансформатора в комплексной форме имеют вид:

;

.

Здесь , , .

Из второго уравнения может быть определен комплекс вторичного тока:

.

Переход от комплекса вторичного тока к его действующему значению дает:

,

откуда может быть определен коэффициент трансформации тока:

.

Из этих соотношений видно, что коэффициент трансформации тока не является постоянной величиной, а зависит от сопротивления нагрузки.

Коэффициент трансформации напряжения также зависит от сопротивления приемника.

После подстановки значения в первое уравнение трансформатора получается выражение первичного тока:

.

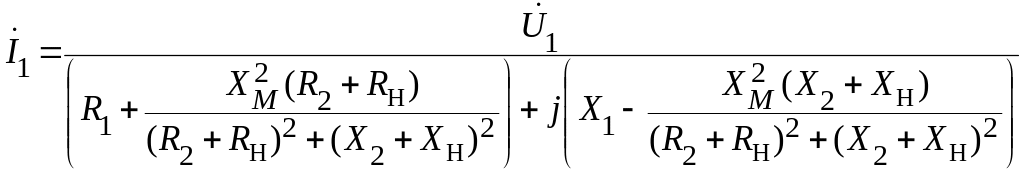Знаменатель этого выражения представляет собой результирующее полное сопротивление цепи, эквивалентной трансформатору.

Результирующее активное сопротивление образует сумма активного сопротивления первичной цепи и сопротивления, вносимого вторичной цепью:

.

Результирующее реактивное сопротивление образует разность реактивного сопротивления первичной цепи и сопротивления, вносимого вторичной цепью:

.

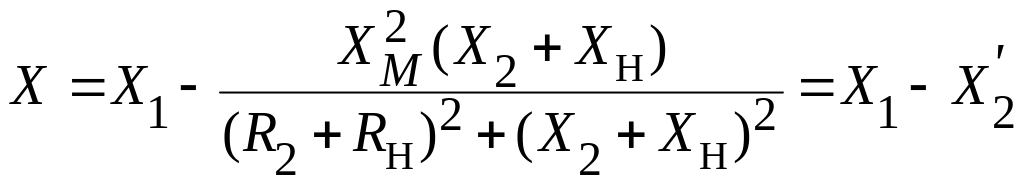Схема двух контуров с индуктивной связью может быть заменена эквивалентной схемой без индуктивной связи.

Для приведенной Т - образной схемы система уравнений по второму закону Кирхгофа для двух контуров в комплексной форме будет иметь вид:

;

.

В случае, когда , то разность т.е. отрицательна, что эквивалентно емкости (повышающий напряжение трансформатор). При , разность становится отрицательной (понижающий напряжение трансформатор).

Периодические несинусоидальные напряжения и токи в линейных цепях Разложение периодических функций в ряд Фурье

Периодическими несинусоидальными токами и напряжениями называют токи и напряжения, изменяющиеся во времени по периодическому несинусоидальному закону. Явления, происходящие в линейных цепях при периодических, несинусоидальных напряжениях и токах проще всего поддаются исследованию, если кривые напряжения или тока разложить в тригонометрический ряд Эйлера - Фурье.

Как известно из курса математики, всякую периодическую функцию с периодом , удовлетворяющую условиям Дирихле, можно разложить в ряд Фурье. Этот ряд состоит из суммы постоянной составляющей А₀ (нулевая гармоника) и синусоид разных частот (гармоник) .

(*)

где k – целые числа, начиная с единицы, - основная частота, Т - период функции.

Здесь составляющая при k = 1 носит название первой гармоники, все остальные члены вида при k > 1 носят название высших гармоник. Гармоники для которых k - нечетное число, называются нечетными, а для которых k - четное число, называются четными.

Суммы синусов с вспомогательными углами можно представить рядом Фурье, имеющим следующую форму:

(**)

Здесь ; .

Коэффициенты могут быть вычислены при помощи следующих интегралов:

; ; .

Постоянная составляющая равна среднему значению функции за ее период .

Зная коэффициенты ряда (**) можно перейти к форме (*), вычисляя

и .

В том случае, если периодическая функция задана не аналитически, а в виде графической кривой, то при разложении ее в ряд Фурье коэффициенты ряда можно отыскать приближенно, заменяя интегралы суммой. В этом случае период Т кривой на графике разбивают на n равных частей, после чего коэффициенты , , находят из выражений, где вместо следует подставить .

; ; .