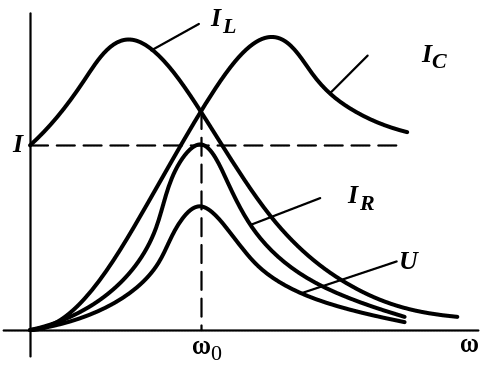
Резонансная характеристика
Покажем зависимости токов на элементах контура от частоты при поддержании тока I = const.
|
Ток через катушку индуктивности:
.
Ток через конденсатор:
.
На резонансной частоте входная проводимость параллельного контура:
,
где
.
Таким образом, входная проводимость параллельного контура, достаточно мала при высокой добротности, что позволяет эффективно подавлять нежелательные частоты.
Цепи с взаимной индукцией
|
Пусть имеем цепь с двумя катушками индуктивности, по одной из которых протекает ток. Этот ток создает в данной катушке магнитный поток, который в свою очередь пересекает площадь витков второй катушки. |
В
этом случае любое изменение тока,
например, в первой катушки вызовет не
только к появлению в ней ЭДС самоиндукции
,
но и к появлению во второй катушке ЭДС
взаимной индукции:
.
Аналогично, изменение тока
второй катушки приведет к появлению в
ней ЭДС самоиндукции
,
а также к появлению в первой катушке
ЭДС взаимной индукции:
.
При
этом
– коэффициент взаимной индукции
(взаимная индуктивность).
Степень индуктивной связи двух индуктивных элементов характеризует коэффициент связи, под которым понимают отношение:
.
Зажимы двух катушек называются одноименными, если при одинаковом направлении токов относительно этих зажимов, магнитные потоки самоиндукции ФL и взаимной индукции ФМ в каждой катушке совпадают по направлению.
Последовательное и параллельное соединения индуктивно связанных катушек
При последовательном соединении катушек ток в них один и тот же, а приложенное напряжение должно преодолеть все ЭДС и сопротивления цепи.
|
Рассмотрим согласное включение катушек, когда магнитные потоки самоиндукции и взаимоиндукции в обеих катушках направлены одинаково. |
В данном случае ЭДС самоиндукции и взаимной индукции имеют одинаковые знаки.
Тогда приложенное напряжение при обходе контура по направлению тока запишется в виде:
.
При встречном включении катушек магнитные потоки самоиндукции и взаимоиндукции направлены в противоположные стороны и ЭДС взаимоиндукции имеет знак, обратный знаку ЭДС самоиндукции. Тогда приложенное напряжение:
В общем виде можно записать:
.
Для синусоидального напряжения и тока подобное соотношение в комплексной форме может быть записано в виде:
.
Следовательно,
результирующая индуктивность всей цепи
при согласном включении:
,
при встречном включении:
.
Векторные диаграммы:
согласное включение |
встречное включение |
|
|
При параллельном соединении катушек их напряжение одинаково.
При выбранных направлениях токов и напряжения, запишем следующую систему уравнений:
Здесь
;
;
.
В этих уравнениях комплексные напряжения вводятся со знаком плюс, так как одинаково ориентированы относительно одноименных зажимов (согласное включение обмоток).
Решая систему относительно токов, получим:
;
;
.
Тогда, входное комплексное сопротивление будет равно:
.
При отсутствии магнитной связи, имеем знакомое соотношение:
.
При
встречном соединении катушек индуктивности,
комплексные напряжения
и
войдут в систему уравнений со знаком
минус и тогда входное сопротивление
цепи примет вид:
.