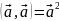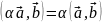1. Действия над матрицами и их свойства.

Произведением матрицы на число λ называется матрица

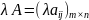
Суммой двух матриц и 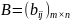называется матрица

Произведение матрицы А на матрицу В в указанном порядке определено только тогда, когда количество столбцов матрицы А равно количеству строк матрицы В ( и )

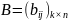Произведением матрицы А на матрицу В называется матрица С , элементы которой находятся по формуле: 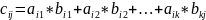, где i=1…m, j=1…n.

Свойства операций над матрицами:

А+В=В+А – коммутативность/переместительное

(А+В)+С=А+(В+С) – ассоциативность/сочетательное

АВ≠ВА – неперестановочная операция

(А+В)С=АС+ВС – дистрибутивность

α(АВ)=(αА)В=А(αВ) – ассоциативность умножения на число

А+0=А

АЕ=ЕА=А

(АВ)^Т=В^ТА^Т

2. Определители 3-го порядка и их свойства.

Определителем з-го порядка или определителем матрицы А называется число

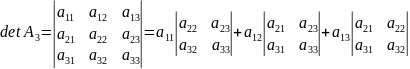
Свойства определителей (верны для строк и столбцов):

Определитель матрицы не меняется при ее транспонировании

Если поменять местами любые две строки определителя, то он изменит знак

Определитель, содержащий две одинаковые строки, равен нулю

Определитель, содержащий нулевую строку равен нулю

Если все элементы какой-либо строки определителя умножить на одно и то же число, то значение определителя также умножится на это число (общий множитель строки можно вынести за знак определителя)

Если соответствующие элементы двух строк определителя пропорциональны, то он равен нулю

Если ко всем элементам какой-либо строки определителя прибавить соответствующие элементы другой строки, умноженные на одно и то же число, то определитель не изменится

Определитель треугольной матрицы равен произведению главной диагонали

Определитель равен сумме произведений всех элементов какой-либо строки на их алгебраические дополнения

Алгебраическое дополнение – минор, взятый со знаком (-1)^i+j

Минор – определитель второго порядка, получаемый из определителя матрицы А путем вычеркивания i-й строки и j-го столбца.

3. Обратная матрица. Матричная запись системы линейных уравнений и её решения.

Матрица А называется невырожденной, если определитель этой матрицы не равен нулю, в противном случае матрица называется вырожденной.

Матрица, обозначаемая А^-1 называется обратной к матрице А, если А^-1А=А А^-1=Е

Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы она была невырожденной.

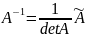
Союзная матрица или присоединенная к матрице А имеет вид

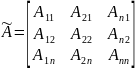
Свойства:

(А^-1)^-1=А

(АВ)^-1=В^-1А^-1

(А^-1)^Т=(А^Т)^-1

Матричная запись системы линейных уравнений:

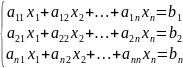
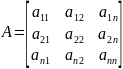
4. Скалярное произведение и его свойства. Угол между векторами. Проекция вектора на ось.

Любые два вектора называются равными, если они имеют одинаковую длину и направление.

Множество всех равных векторов называют свободным вектором.

Угол между векторами – наименьший из двух смежных углов, приведенный к общему началу (0≤α≤180)

Скалярным произведением векторов а и b называется число, обозначаемое (a,b), равное произведению длин этих векторов на косинус угла между ними.

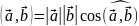
Свойства:

1. 

2. 

3. 

4. 

Координаты вектора в прямоугольной системе координат есть проекция этого вектора на координатные оси.