8. Теорема Бернулли.

Пусть с.в. X ~ В(n, р).

Тогда где –const>0. (7)

Доказательство. Эта теорема является следствием теоремы Хинчина, т.к. где X_i ~ В(1,р) и все X_i – независимые с.в.;

УЗБЧ - усиленный закон больших чисел.

(8)

(Это сходимость почти наверное (п.н.) или с вероятностью 1).

Теорема Колмогорова.

Пусть Х₁,Х₂,...,Х_n – независимые с.в. и . Тогда последова– тельность с.в. {X_i.} подчиняется УЗБЧ (8). (Без доказательства).

п3. Задачи

Задача 1.

Средний срок службы мотора 4 года. Оценить вероятность того, что мотор прослужит < 20 лет.

Решение.

По (2б) Р{Х < 20}  1 – = 0.8, где с.в. Х – срок службы мотора.

Задача 2.

Средняя сумма всех вкладов в сберкассу = 20 000 руб., а вероятность того, что случайно взятый вклад окажется < 100 руб. = 0.8. Оценить число вкладчиков n, если размеры вкладов одинаково распределены.

Решение.

По (2б) P{X<100}=0,8  1–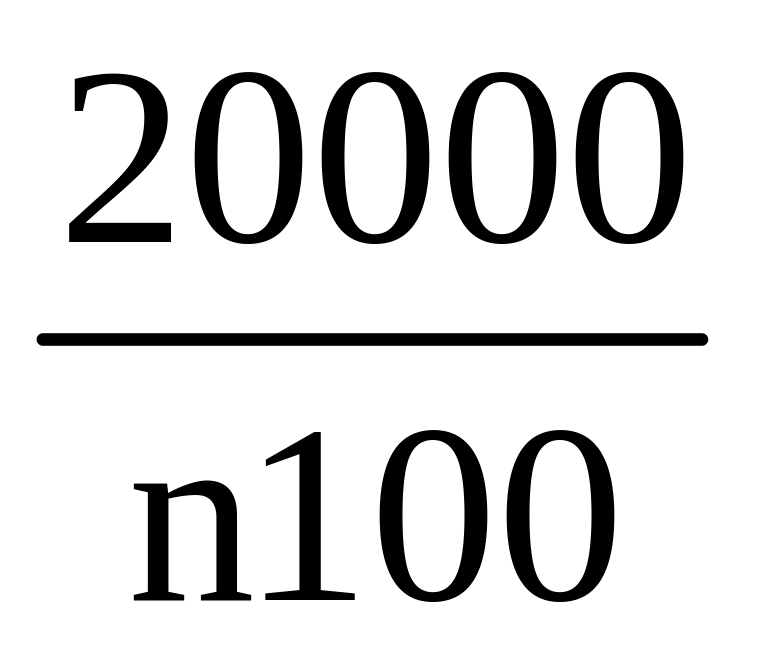   0,2  n  1000, т.к. MX = 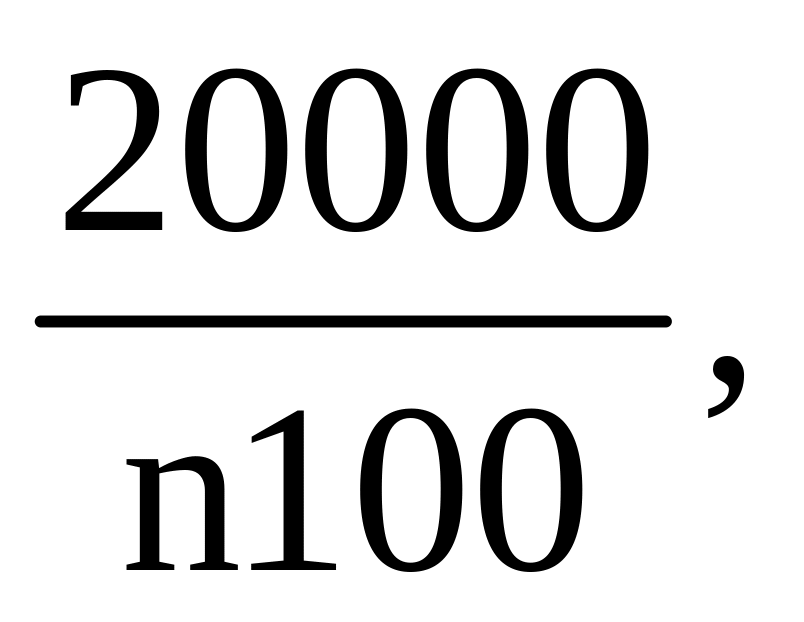где с.в. Х – размер случайного вклада.

Задача 3.

В сети 18000 ламп. Вероятность быть включенной для каждой лампы 0.9. Оценить вероятность того, что число включенных ламп отличается от своего среднего X менее, чем на 200 ламп.

Решение.

Пусть с.в. Х – число включенных ламп, тогда по (3б) имеем:

т.к. с.в. X ~ В(n, р), n=18000, p=0.9, MX= np = 16200, DX= npq = 1620.

Задача 4.

Оценить вероятность того, что частота появления герба при 100 бросани–ях монеты отклонится от своей вероятности менее чем на  = 0.1.

Решение.

По (4) (при Х – число гербов ,  = 0.1) , имеем:

т.к. X ~ В(n, р), MX = np, DX = npq, n = 100, p = 0.5 .

Задача 5.

Распределение с.в. Х задано рядом распределения.

X	2	4	6	8	12
P	0.2	0.3	0.25	0.2	0.05

Вычислить точно и оценить по (2б) Р(Х < 11).

Решение.

По данному ряду распределения Р{Х < 11} = 1– 0.05 = 0.95. По (2б):

Замечание. Эта задача иллюстрирует грубость оценки по неравенству Мар-кова по сравнению с точным значением P(X<11).

Задача 6.

Оценить вероятность того, что с.в. X отклонится от MX менее, чем на 3 в случаях а) X ~ R[a,b]; б) X ~ N(a, b) в сравнении с вероятностями этого события.

Решение.

1. X ~ R[a,b]. По (3б) получаем:

В то же время для X ~ R[a,b] имеем:

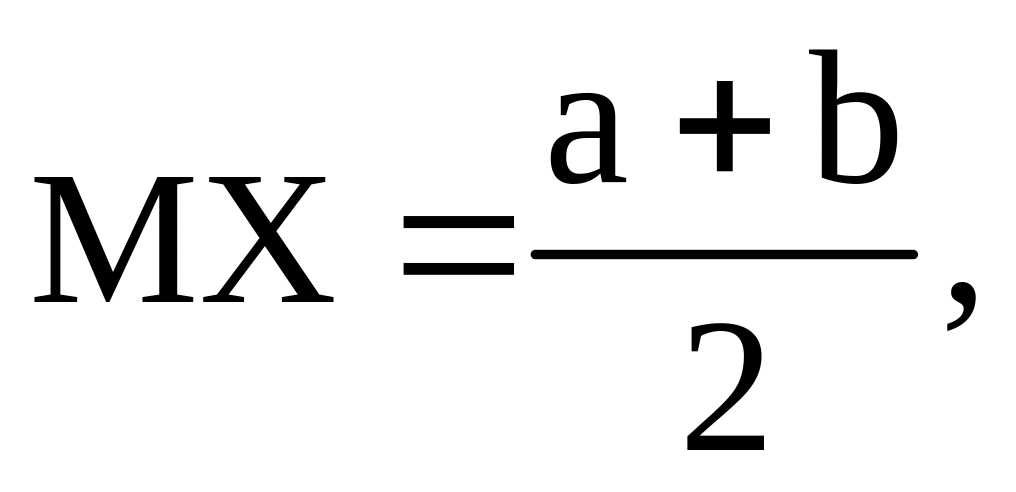
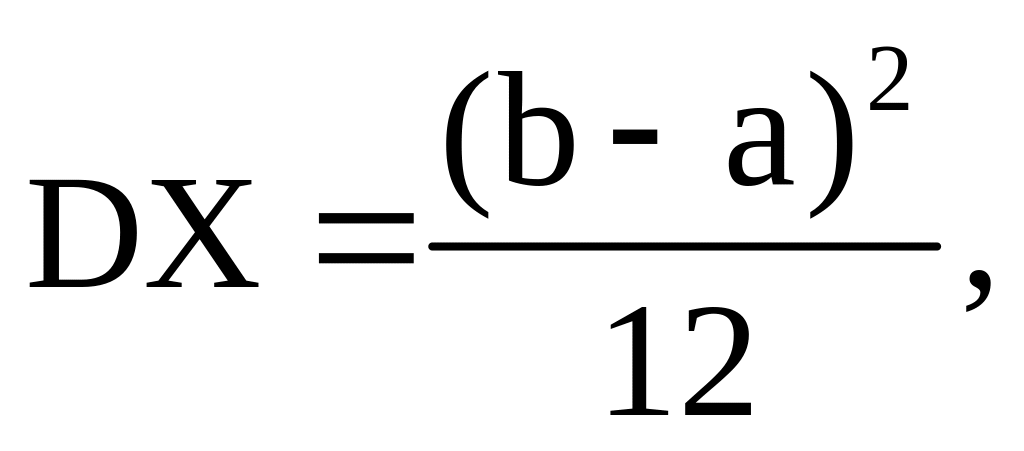
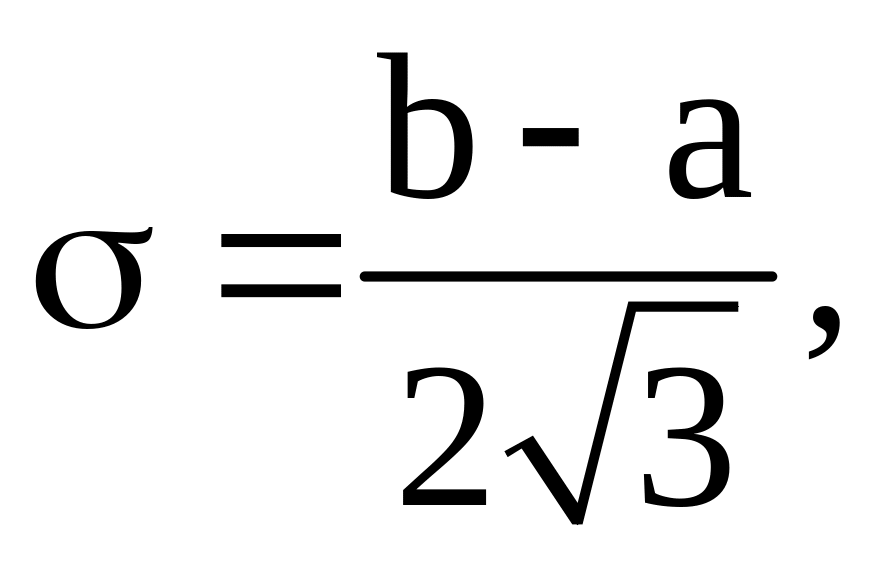
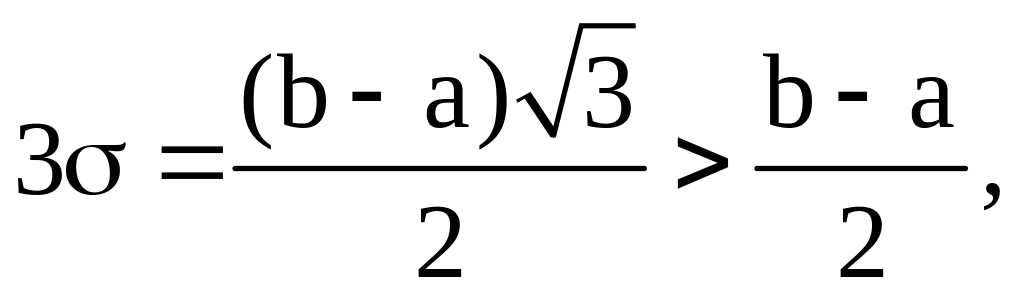поэтому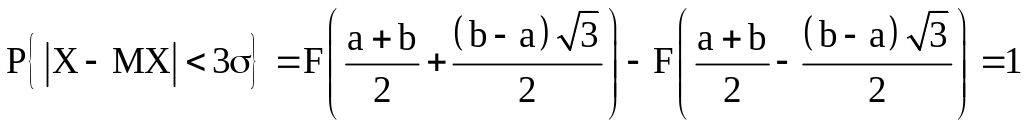

т.к.

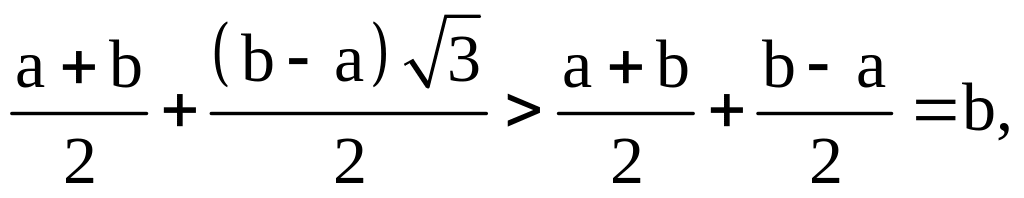
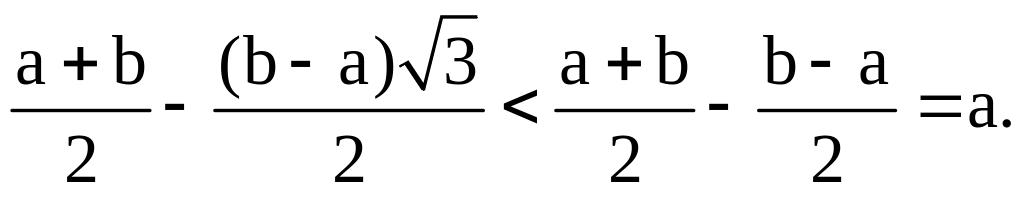
б) X ~ N(a, b). По (3б) получаем:

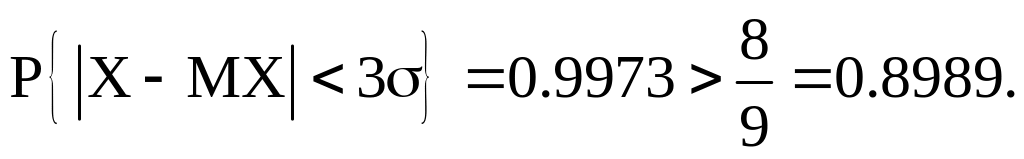
Эта задача иллюстрирует грубость оценки НЧ.

Задача 7.

Пусть с.в. X ~ G(р). Оценить Р{|Х – MX| }.

Решение.

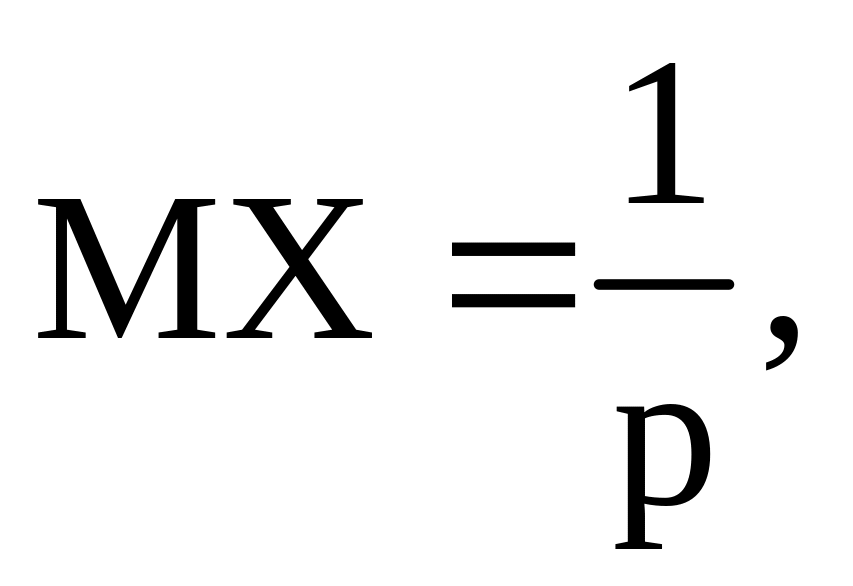
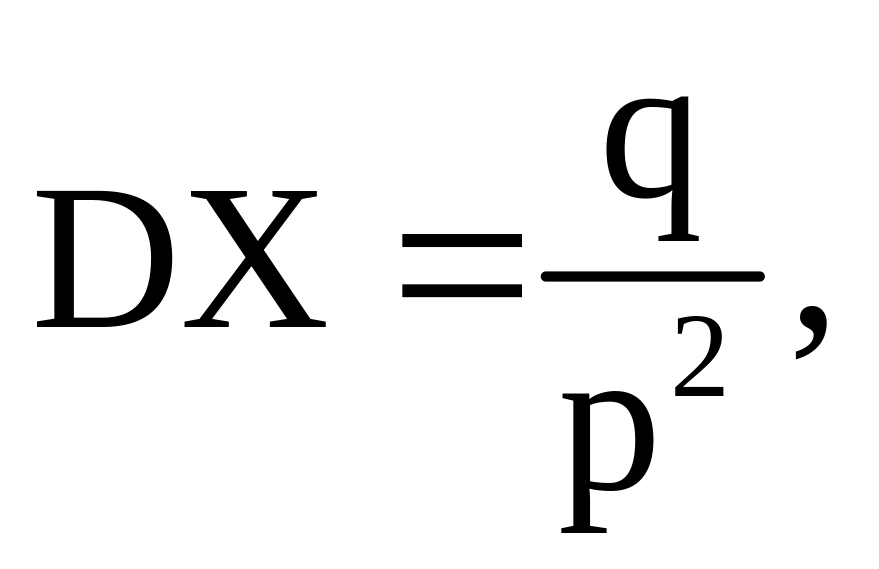где q = 1 – р. По (За) имеем:

При (что можно сделать за счет выбора ) мы имеем тривиальную оценку:

Эта задача иллюстрирует грубость неравенства Чебышева.

Задача 8.

Пусть {X_i} – независимые с.в.. Применим ли к ним ЗБЧ в следующих случаях?

Xn	–2	0	2
P	1/ 4	1/ 2	1/ 4

Решение.

MX_n= 0 < С = 1 и с.в. одинаково распределены, следовательно по теореме Хинчина ЗБЧ применим.

Задача 9.

Пусть {X _i} – независимые с.в.. Применим ли к ним ЗБЧ в следующем случае?

Xn	–5n2	0	5n2
P	1 / 3 n2	1 – n2 2 / 3	1 / 3 n2

Решение.

С.в. {X _n} – независимы, а т.к. имеют равно–мерно ограниченные дисперсии, поэтому ЗБЧ применим.

Задача 10.

Х – число гербов, выпавших при бросании монеты, Y – число выпавших очков на игральной кости. Оценить вероятность того, что X+Y < 14.

Решение.

С.в. X ~ B(n, p), где n = 10, р = 0.5, MX = np = 5,

MY= (1+2+3+4+5+6) =3,5.

По неравенству Маркова (2б)

Задача 11.

В партии n изделий с первого станка и m изделий со второго станка. По неравен– ству Чебышева оценить вероятность того, что число X первосортных изделий в партии отличается от своего среднего по абсолютной величине менее, чем на , если вероятности изделий первого сорта с первого и второго станков, соответ– ственно равны r и s.

Решение.

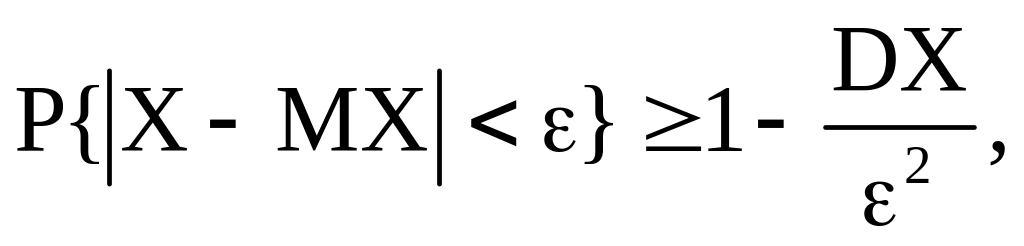
где Х₁ и Х₂ – количество пер-восортных изделий в партии с соответственно 1^ого и 2^ого _{станков.} С.в. Х₁ ~ B(n,r), Х₂ ~ B(m, s)  MX₁ = nr; MX₂ = ms; MX = nr + ms; DX₁ = nr (1 – r); DX₂= ms (1 – s); DX= nr (l – r) + ms (l – s). Поэтому

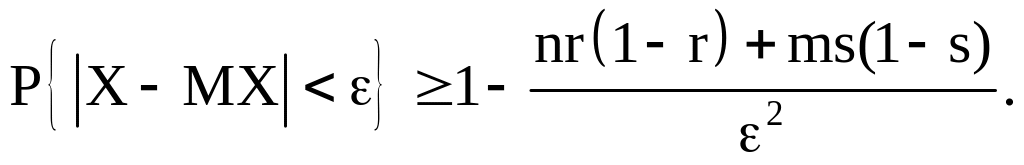
Задача 12.

Пусть {Х_i} – независимые с.в. Применим ли к ним ЗБЧ в следующем случае?

Х n		0
P

Решение.

условие теоремы Чебышева не выпол-няется. Проверим выполнение условий теоремы Маркова:

ЗБЧ применим по теореме Маркова.