4. Обобщенное неравенство Чебышева.
Пусть X1, X2,...,Xn – независимые с.в. с математическими ожиданиями MX1, MX2 ,..., MXn и дисперсиями 12 , 22 , ... , n2 соответственно, тогда
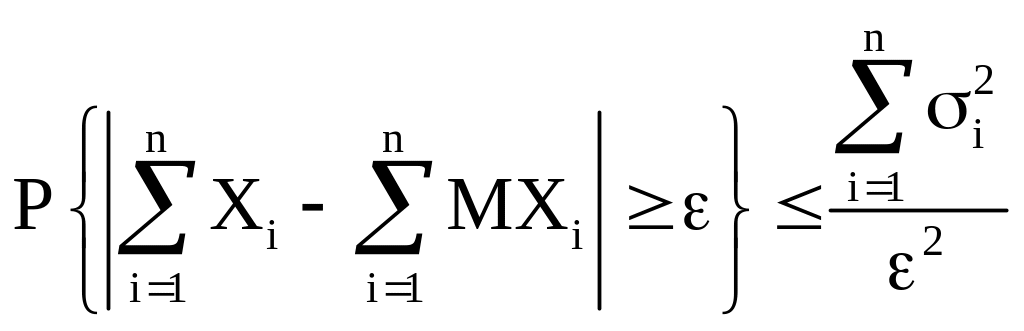(4а)
или
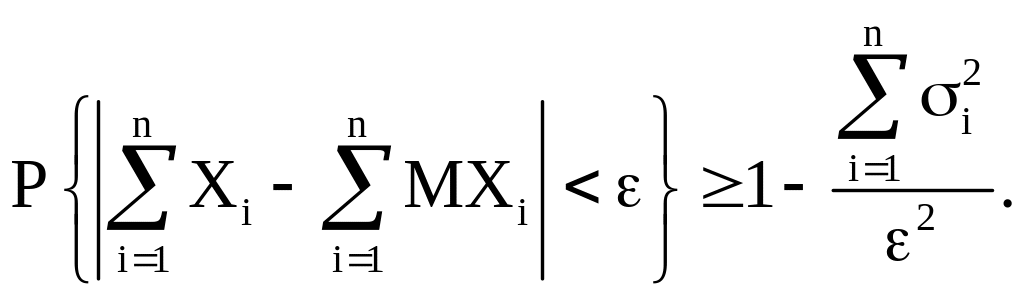(4б)
Доказательство. Очевидно, что (4а) и (4б) эквивалентны.
Обозначим
,
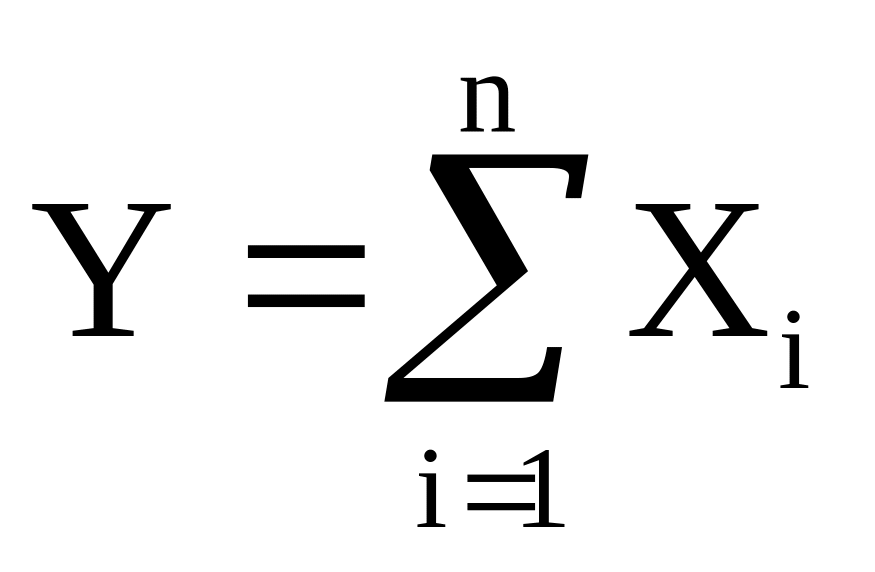тогда (4а) и (4б) получаются соответственно
из (За) и (36) как следствия.
П 2. Теоремы группы збч
Теперь рассмотрим теоремы группы ЗБЧ, объеденные тем, что все они формулируют условия, при которых данная последовательность с.в. подчиняется ЗБЧ. Различия условий в теоремах определяются разными свойствами исходных последовательностей с.в.
Приведем наиболее простые теоремы группы ЗБЧ, дающие достаточные условия выполнимости ЗБЧ для данных последовательностей с.в. Это значит, что на основании этих теорем, при выполнении их условий можно утверждать, что к данным последовательностям с.в. применим ЗБЧ. Если же условия этих теорем выполняться не будут, то исследования о применяе– мости ЗБЧ нужно продолжить на основании других теорем. Теоремы будут далее представлены в порядке их усиления.
5. Теорема Хинчина.
Пусть Х1, Х2, ...,Хn – независимые одинаково распределенные с.в. с конеч– ным математическим ожиданием MX.
Тогда
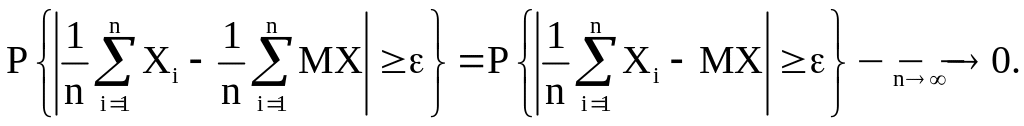(5)
Это ЗБЧ в форме Хинчина.
Доказательство. Приведем сначала в случае конечности DX. В общем слу-чае доказательство проводится методом характеристических функций. Воспользуемся неравенством Чебышева (За):
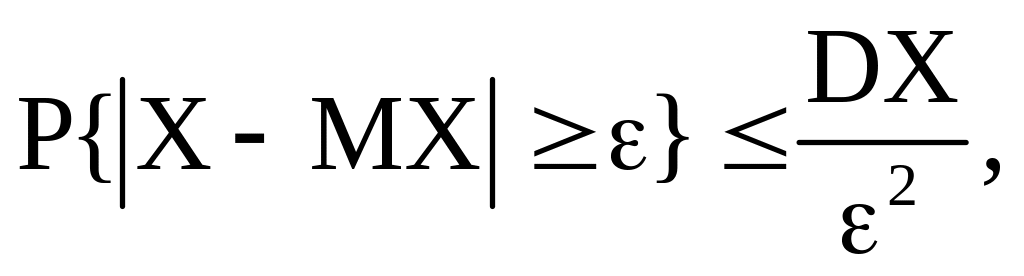где
X
с.в.
> 0,
–
const
>
0.
Положив
имеем
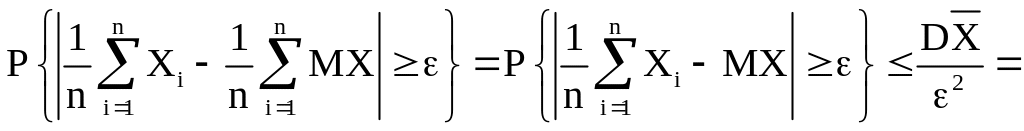
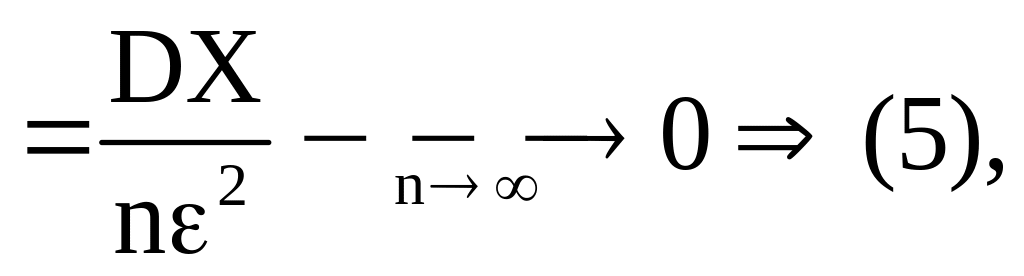т.к.
Доказательство теоремы Хинчина в общем случае (методом характерис– тических функций).
Обозначим
Тогда утверждение теоремы Хинчина
можно записать в виде
или
(сходимость по вероятности).
Введем
в рассмотрение
характеристические функции с.в. Х1,
Х2,
...,Хn:
.
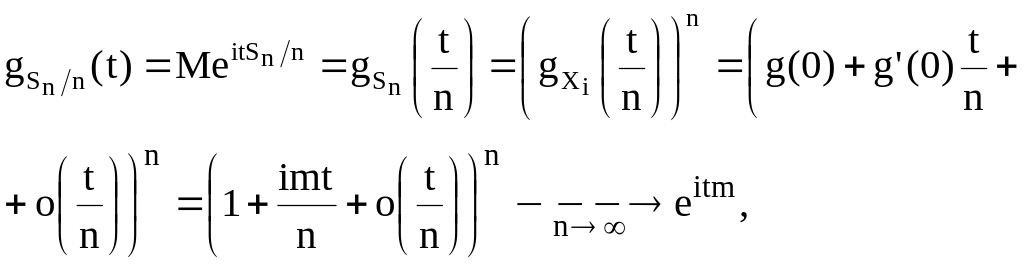
а
это характеристическая функция
константы =
m,
т.е. доказана сходимость
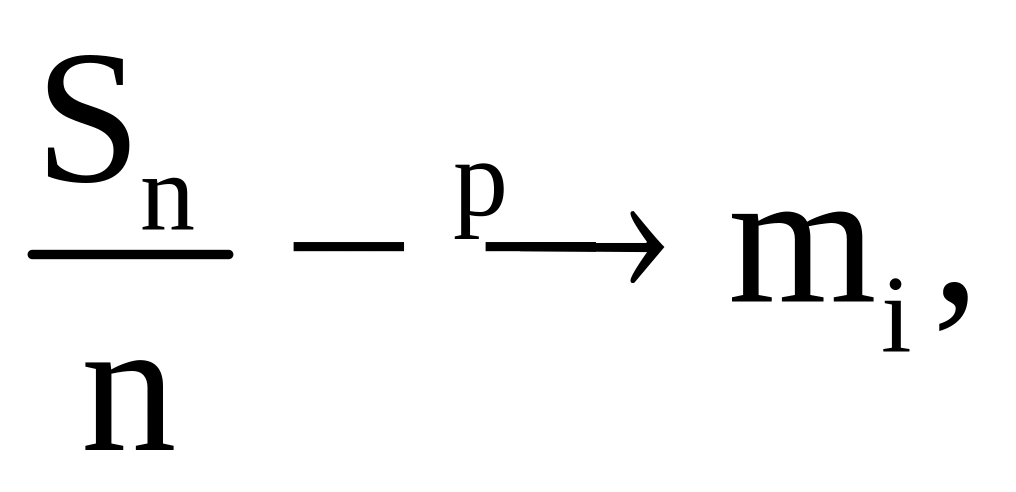т.е.
сходимость по распределению, а т.к. m
– константа,
то эта схо–димость эквивалентна
сходимости по вероятности, что и
утверждается в доказыва– емой теореме.
6. Теорема Чебышева.
Пусть X1,X2,...,Xn – независимые с.в., имеющие равномерно ограниченные дисперсии, т.е. существует const С такая, что DXi С для всех i = 1, 2, ... . Тогда последовательность с.в. {Xi.} подчиняется ЗБЧ в форме (1).
Доказательство.
По
(За)
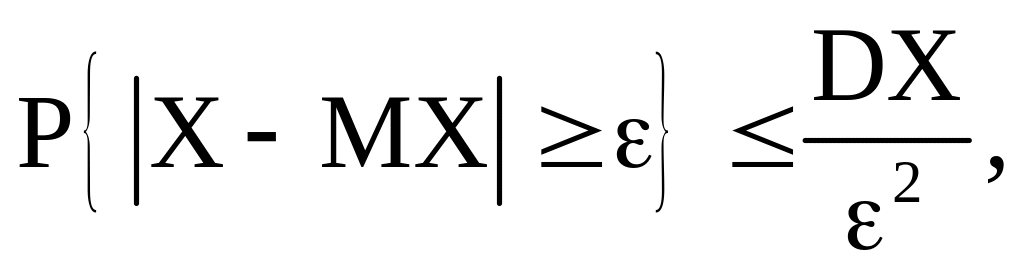где
–const
> 0.
Пусть
Тогда
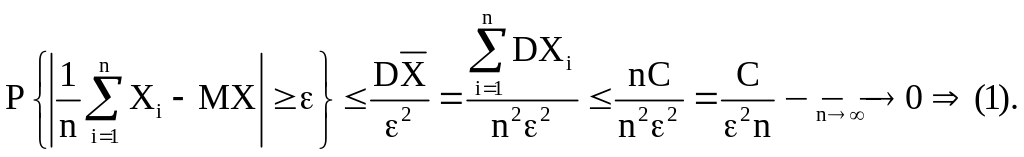
7. Теорема Маркова.
Пусть
с.в. Х1,Х2,...,Хn
–
как угодно зависимые с.в. и
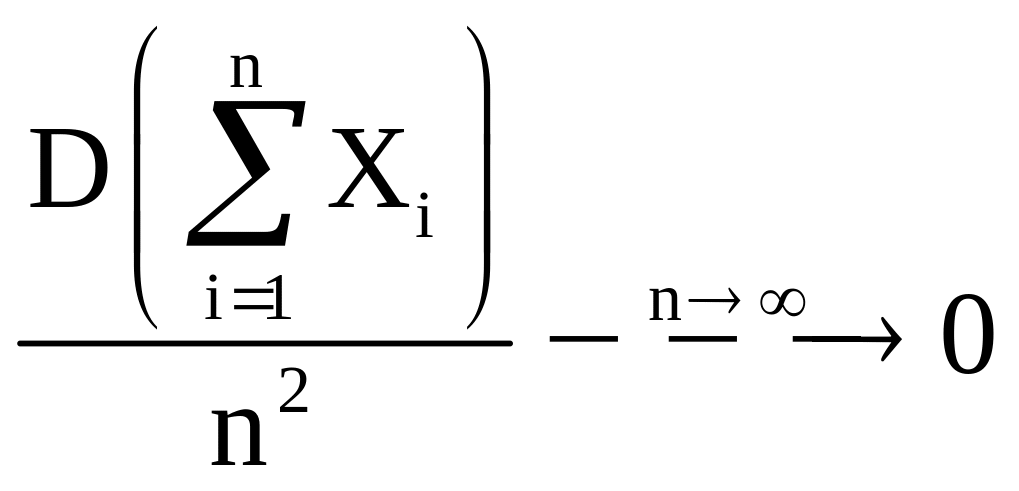(или
где
).
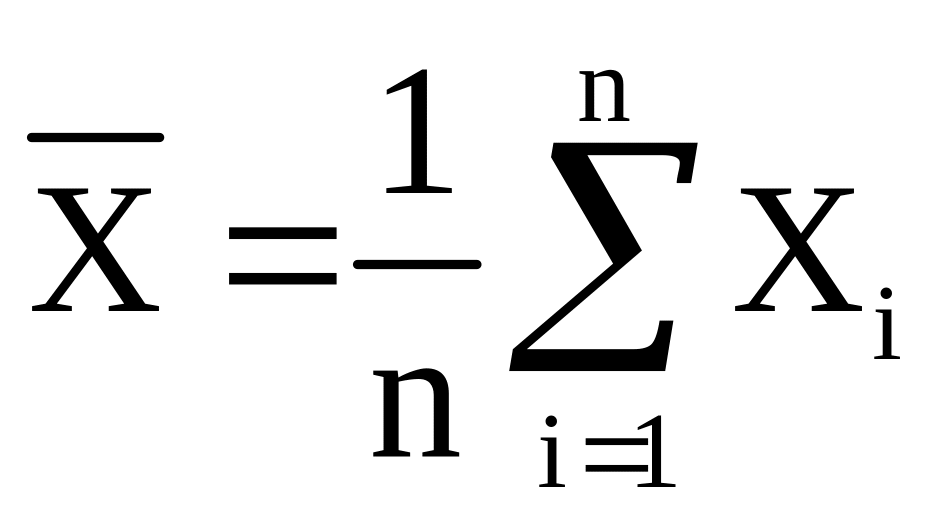Тогда последовательность с.в. {Хi.}
подчиняется ЗБЧ.
Доказательство. По (3а) где X с.в., - const > 0
Пусть
тогда
