§2 Закон больших чисел (збч)

Методы п.ф. и х.ф. широко применяются при доказательстве предельных теорем теории вероятности – группы теорем, устанавливающих закономерности случайных явлений, проявляющихся при большом числе случайных величин (с.в.). Они могут выражаться в установлении соответствия между экспериментальными и теоретичес-кими характеристиками усредненных с.в. (например ЗБЧ, УЗБЧ) или предельных законов распределения некоторых функционалов с.в., зависящих от их числа (например, ЦТП).

п1. Неравенства группы ЗБЧ

Закон больших чисел (ЗБЧ) отражает устойчивость среднего арифметического большого числа случайных величин относительно среднего арифметического их математических ожиданий.

1. Определение и суть збч.

Обозначим

ЗБЧ: 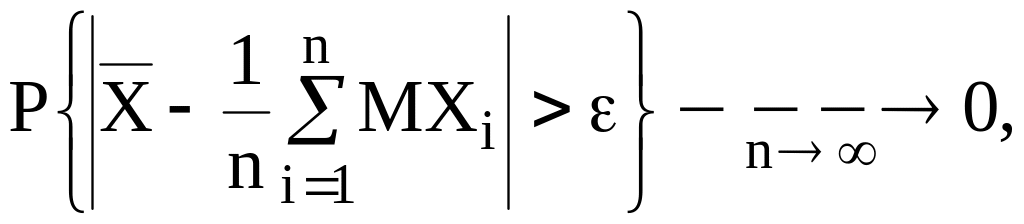(1)

{Х} – cлучайная величина,  - const > 0, или (1) можно записать так

(сходимость по вероятности)

Суть ЗБЧ в том, что совместное действие большого числа случайных факторов при некоторых весьма общих условиях приводит к результату, почти не зависящему от случая.

2. Неравенство Маркова (нм) .

Пусть с.в. Х > 0,  – const 0, тогда

(2а)

или (2б)

Доказательство (1 вар.). Очевидно, что (2а) и (2б) эквивалентны,

a) Пусть Х – дискретная случайная величина с рядом распределения:

X	x1	x2	. . .	xn	. . .
P	p1	p2	. . .	pn	. . .

и пусть такая, что x_1, x₂, …, x_n <   x_k+1, ..., x_n.

Тогда МХ = x₁ p₁+ . . . + x_k p_k+ x_k+1 p_k+1 + . . . + x_n p_n + . . .   (p_k+1 + . . .+ + p_n + . . .) = P{X  }  (2а).

б) Пусть Х – непрерывная с.в. с плотностью распределения f(x),  — const . Тогда

Доказательство (2 вар.). 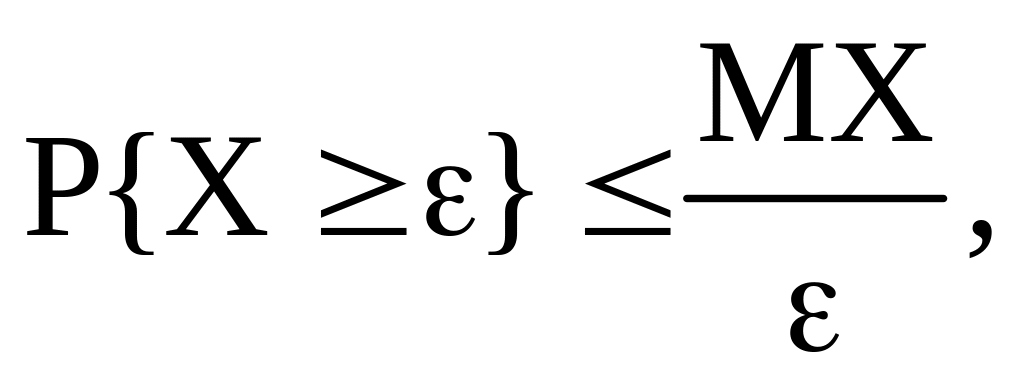где Х – с.в. 0,  – const > 0.

Построим новую с.в.

Тогда MX  MY = 0P{X < } + P{X  } = P{X  }  P{X  }  , что и утверждалось.

3. Неравенство Чебышева (нч).

Если случайная величина Х имеет дисперсию, то при любом  > 0 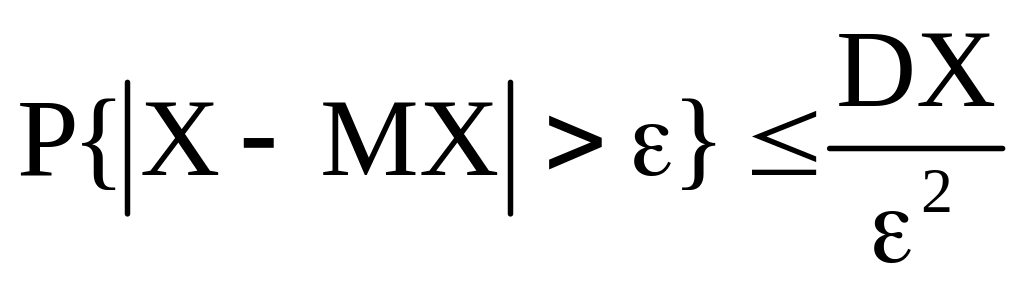(3а)

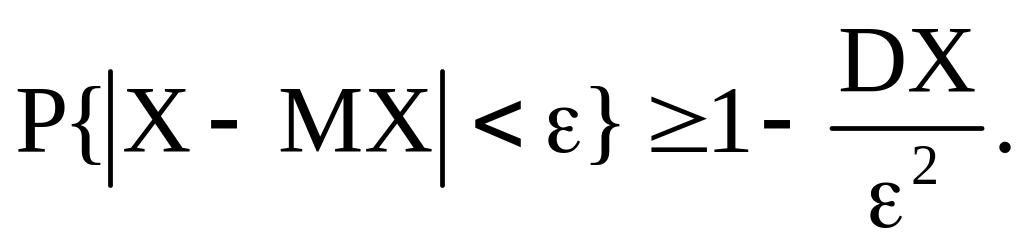или (3б)

Доказательство (1 вар.). Пусть Y = X – MX. Применим к Y² ≥ 0 неравен – ство Маркова в форме (2б), т.к. Y² ≥ 0.

или

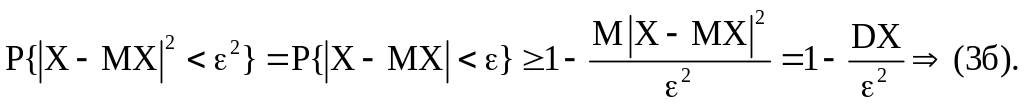
Очевидно, что (За) и (36) эквивалентны.

Доказательство (2 вар.). Докажем НЧ в форме (3а):

Построим новую с.в.

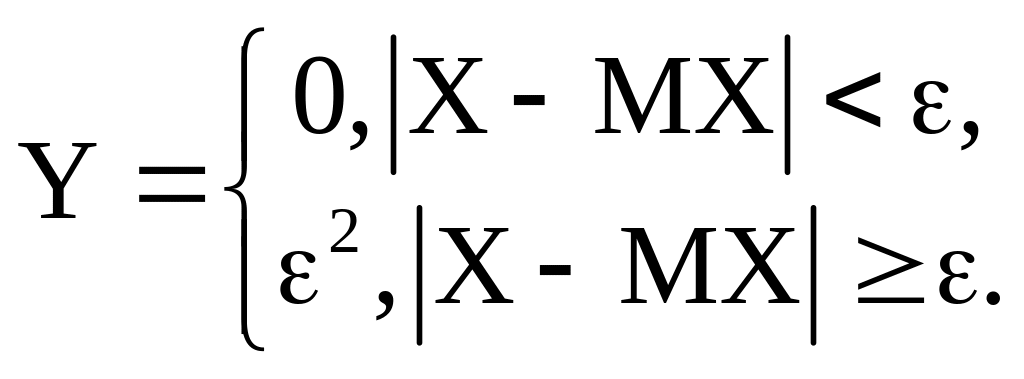
Тогда DX = M(X – MX)²  MY = 0P(|X – MX| < ) + ² P(|X – MX|  ) = ² P(|X – MX|  )  P( |X – MX|  )  , что и требовалось доказать.

Пример на неравенство Чебышева.

Пусть с.в. X ~ В(n, р). Оценим по неравенству Чебышева (3б)

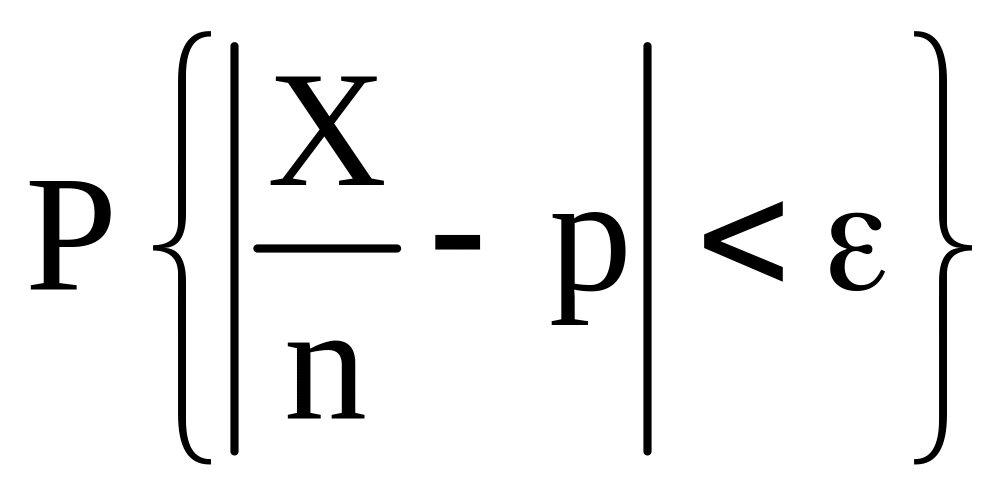, где MX = np; DX = npq; поэтому

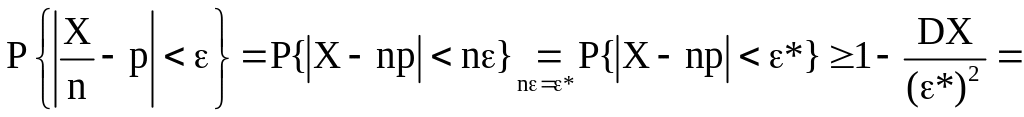
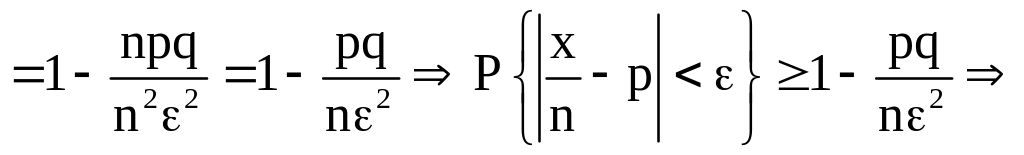
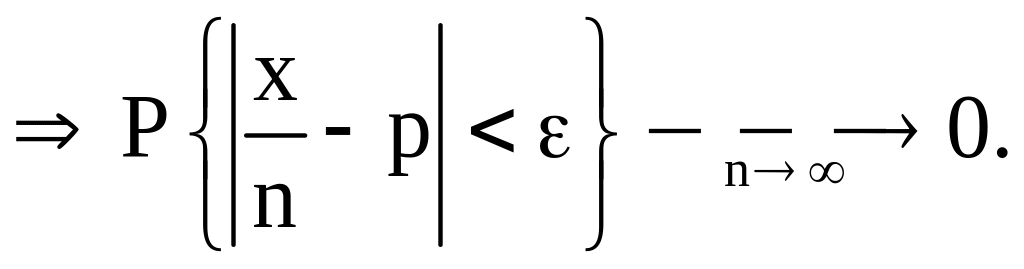(Теорема Бернулли)

Замечание 1.

Неравенства Чебышева и Маркова достаточно грубы, но их значение состоит в возможности получения оценок вероятностей по первым двум моментам, а также в их простоте и универсальности. Кроме того, неравенство Чебышева используется при доказательстве теорем группы ЗБЧ. Надо иметь в виду грубость неравенств Чебышева и Маркова, которая ниже будет проиллюстри– рована примерами.