6. Теоремы о характеристических функциях.

1) Пусть a₁, … , a_n – постоянные , харак-теристические функции. Тогда – тоже характеристичес-кие функции.

2) Произведение характеристических функций – тоже характеристическая функция.

3) Единственной характеристической функцией, такой, что g(t) = 1+o(t²), при является

4) Если g(t) – характеристическая функция и имеет , то она везде имеет и .

5) Теорема Пойя. Если – непрерывна, четна и выпукла книзу при g(t)≥1, g(0) = 1, g(t), при , то g(t) – характеристическая функ-ция.

6) Теорема Марцинкевича. Если g(t) – характеристическая функция имеет вид , где P(t) – полином, то его степень ≤ 2.

7) Re g(t) – характеристическая функция, если g(t) – характеристическая функция.

8) Если g(t) – характеристическая функция невырожденного распре-деления и а < 0 , то (g(t))^a не является характеристической функцией.

9) Из свойства 3) следует, что, если характеристическая функция действи-тельна, то четна.

10) Если g(t) – характеристическая функция, то тоже характе-ристическая функция.

7. Примеры на распознавание характеристических функций по свойствам и теоремам.

Являются ли характеристическими функциями слeдующие функции g(t) (Если ДА, то чему они соответствуют?)

Задача1.

f(t)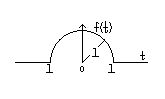

Ответ: НЕТ (по 4), в точках (-1, 0) и (1, 0) нет и

Задача 2.

целое.

Ответ: НЕТ при (по 6); ДА при : X ~ N(0, ); НЕТ при (по 9).

Задача 3.

g(t) = cos² t.

Ответ: ДА, т.к. – х.ф.с.в.

	-2	0	2
P	1/4	1/2	1/4

где :

Задача 4.

Ответ: ДА по 5, это закон Коши.

Задача 5.

Ответ: ДА – это характеристическая функция с.в. Х ~

Задача 6.

Ответ: НЕТ по 9.

Задача 7.

Ответ: ДА по 6: ~ Х ~ N(0,1).

п3. Задачи

Освоение этой темы требует большого числа разных задач на свойства п.ф. и х.ф. Решения ниже приведённых задач в основном не представляют трудности, т.к. объяснены теоретически и на примерах в предыдущих пунктах этого параграфа, поэтому предлагаются для самостоятельного решения, а отдельные, более сложные с решениями.

Задача 1.

Найти п.ф. основных распределений дискретного типа и их моменты (МПФ).

а) Х= С – const; б) X ~ B(1,p); в) X ~ B(n,p); г) X_i ~

д) X_i ~ е) X_i ~ сд ж) Z₁ ~ Па(r,p); ж) Z₂ ~ OB(r,p).

Задача 2.

Найти п.ф. с.в. где {X_i} – независимые с.в. и

а) X_i ~ B(n = 5, p = 0,4), m = 1, a = 3, b = –2;

б) X_i ~ m = 3, a = –4, a = 5, a = 1, b = –3;

в) X_i ~ 1,2,3,4; m = 4, a = –1, a = 2, a = –5, a = –3,

b = –2.

Задача 3.

где Y,X₁,X₂, …, X_n – независимые с.в., имеющие п.ф., одинаково распределены.

Найти п.ф. и моменты (МХ и DX) с.в. Z в следующих случаях:

а) X ~ B(n = 3, p₁ = 0,6), Y ~ G(p₂ = 0,3);

б) X_i ~ Y ~

в) X_i ~ Y ~ cдG(p = 0,4);

г) X_i ~ G(p = 0,5), Y ~

д) X_i ~ cдG(p₁ = 0,1), Y ~ B(n = 2, p₁ = 0,2);

е) X_i ~ Па(r = 4, p₁ = 0,3), Y ~ B(n = 1, p₂ = 0,3);

ж)

Xi	1	2	3
P	0,3	0,4	0,3

;

Y ~

Задача 4

Методом п.ф. найти композиции следующих с.в.:

а) X ~ Y ~

б) X ~ B(n₁, p), Y ~ B(n₂, p).

Задача 5.

Какие из данных функций являются п.ф., если «да», то каким распреде-лениям они соответствуют?

а) V(s)= 0,5+0,4s²; б) V(s)= 0,3+0,2s+0,1s²+0,4s⁵;

в) V(s)= 0,5{1 + exp (3(s – 1))}; г) V(s)= 0,8+(0,4s + 0,6)³ + 0,2;

д) V(s)= ехр{2(1+exp(3(s – 1) – 1)}; е) V(s)= s²(0,3s² + 0,7)⁵;

ж) V(s)= s² exp{4(s³ – 1)}; з) V(s)= 0,001s⁴/(1 –0,9s³)³.

Задача 6.

Используя связь х.ф. с п.ф., найти х.ф. с.в. с распределением, указанным в Задаче 1.

Задача 7.

Найти х.ф. следующих распределений:

а) X ~ R[a,b]; б) X ~ R[–a,a]; в) X ~ E[L];

Задача 8.

Зная х.ф. с.в. X₀ ~ N(0,1), найти х.ф. с.в. X ~ N(a,b);

Задача 9.

Найти х.ф. с.в. если:

а) X ~ Y = 3x – 2; б) X ~ N(a,b), Y = X – 1;

в) X ~ R[0,1], Y = 1 – 2x; г) X ~ B(n,p), Y = 3 – X;

Задача 10.

Методом х.ф. найти моменты (MX и DX) основных распределений задачи 1 а также для X ~ N(a,b), X ~ R[a,b] и X ~ E[L].

Задача 11.

где Y, X₁, X₂, … , X_n – независимые с.в., с.в. Y имеет п.ф. с.в. {X_i} одинаково распределены. Методом х.ф. найти х.ф. с.в. Z и её моменты MZ и DZ в случаях задачи 4, а также в случаях:

а) X ~ N(0,1), Y ~

б) X ~ R[–2,2], Y ~

Задача 12.

Методом х.ф. найти композиции с.в. задачи 4 и следующих с.в.:

а) X ~ N(a₁,b₁), Y ~ N(a₂,b₂);

б) X ~ E[L₁], Y ~ E[L₂].

Задача 13.

Какие из функций являются х.ф., если «да», то каким распределениям они соответствуют?

а) g(t) = 0,1+0,2exp{it} + 0,7exp{8it}; е) g(t) = exp{t(2i – nt)};

б) g(t) = 0,2(0,1exp{it} + 0,7+0,8exp{it – 1}); ж) g(t) = cos t;

в) g(t) = exp{4it} cos3t; з) g(t) = t;

г) и) g(t) = (sint)/t;

д) g(t) = exp{–100it}; к) g(t) = sint;

л) g(t) = exp{–t/4n};

Задача 14.

X₁, X₂, … , X_n – независимые одинаково распределенные с.в. и X_k ~ R[–1,1] для любого k = 1,…,n. Методом х.ф. найти предельный закон распределения с.в. при n т.е. где

т.е. распределение с.в. сходится к N(0,1).

Решение задач на распознавание п.ф. и х.ф.

Задача 15.

а) V(s) – не п.ф., т.к. V(1) ≠ 1 ;

X	0	1	2	5
P	0,3	0,2	0,1	0,4

б) V(s) п.ф. с.в. X:

в) V(s) = где ~ _{EMBED Equation.3} Y ~ B(1;0,5), Z= – одинаково распределённые с.в., и Y,X₁,X₂,…,X_n – независимы c.в. и

г) V(s) = п.ф. с.в. Z = из свойства 6 п.ф., где ~ B(3;0,4), Y ~ B(1;0,8);

д) V(s) = п.ф. с.в. Z = из свойства 6 п.ф., где ~ Y ~

е) – одинаково распределенные и независимые , тогда п.ф. с.в. L, где ~ B(5;0,3), n = 5, a = 2, b = 2;

ж) – одинаково распределенные и независимые с.в. Тогда п.ф. с.в. L, где ~ n = 5, a = 3, b = 2;

з) – одинаково распределенные и независимые с.в. ~ сдG(0,1), n = 3, a = 3, b = 4.

Задача 16.

а) g(t) – х.ф. с.в. Х рядом c распределения;

Х	0	1	8
Р	0,1	0,2	0,7

б) g(t) = g_z(t) = a₁g_z(t) + a₂g_z(t), где a₁ = 0.2, a₂ = 0,8g_x(t) =

= 0,3exp{it} + 0,7 ,

~ B(1;0,3), Y ~

в) g(t) = g_z(t) = g_x(t)g_y(t), где X и Y – независимые с.в.,

g_x(t) = exp{4it};

Y	–3	3
P	0,5	0,5

Z = X + Y;

г) g(t) = g_z(t) = g_x(t)g_y(t), где X и Y – независимые с.в.

Z=X+Y;

д) g(t) – х.ф. с.в. X = –100;

е) g(t) – х.ф. с.в. X ~ N(a = 2, b =

ж) g(t) =

Х	–2	2
Р	1/4	1/4

ряд распределения с.в. Х

з) g(t) – не х.ф., т.к. |g(t)| 1, если g(t) – х.ф.;

и) g(t) – х.ф. с.в. X ~ R[–1,1];

к) g(t) = sin t – действительная и нечетная функция, а действительная х.ф. обязательно четная.

л) g(t) – х.ф. с.в. X ~ N(0; 1/