3. Примеры.
Пример 1. Получить вид производящей функции для следующих распре-делений:
а)
B(1,p);
б)
B(n,
p);
в)
;
г)
G(р);
д)
cдG(р);
е)
Па(r,
p);
ж) OB(r, p).
|
0 |
1 |
P |
q |
p |
б) С.в. Х B(n, p);
1
способ.
где
{Xi}
– независимые
одинаково распределенные случайные
величины по B(1,
p).
Поэтому
по свойству 4
2 способ. Можно вычислит непосредственно
в)
С.в.
Х
;
г) С.в. Х G(р);
Задание. Для остальных распределений найти производящие функции самостоятельно.
Указание. Для е) и ж) использовать их связи с распределениями г) и д) и воспользоваться свойством 4.
Композицией называется закон распределения суммы независимых слу-чайных величин. С использованием свойства 4 задачи для композиций решаются просто.
Метод производящих функций состоит в использовании перечисленных свойств производящей функции.
Пример 2. Найти композиции и моменты для следующих законов распре-деления:
a)
X
,
Y
;
б) X ~ B(n1,p), Y B(n2,p).
(Случайные величины и независимы)
Решение.
а)
закон
распределения с.в. X
+Y
снова
б) решить самостоятельно.
Пример 3. По формулам свойства вычислить моменты распределений:
а)
X
B(1,p);
б)
X
B(n,
p);
в)
X
г)
X
G(р);
д) X cдG(р); е) X Па(r, p); ж) X OB(r, p).
Решение.
б) MX
=
MX
= n
DX=
Задание. Остальные пункты примера решить самостоятельно.
Пример 4. Найти распределение и моменты случайных величин Z струк-туры свойства 6 в случаях:
а) X , Y B(n, p); б) X Y ; в) X G(р), Y B(n, p); г) X B(n, p), Y Па(r, p); д) X OB(r, p), Y B(1, p).
Указание. При решении использовать свойства 6 и 8.
Решение.
а)
где
{Xi}
– независимые
одинаково распределен-ные с.в., {Xi}
и
Y
–
независимы.
производящая
функция случайных величин Z
или закона распределения случайных
величин Z.
MZ = MX∙MY = λnp; DZ = DY(MX)2 + DX∙MY = npqλ2 + λnp =
= npλ (qλ+1).
Задание. Остальные пункты примера решить самостоятельно.
п2. Метод характеристических функций
Определение.
Характеристической
функцией (х.ф.)
случайной величины (с.в.)
назы-вается функция
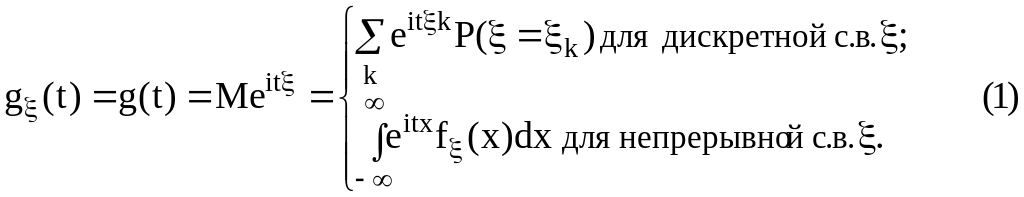
1. Свойства характеристических функций.
1) g(0) = 1. Очевидно следует из определения (1).
2)
т.к.
3)
т.к.
4) g(t) – равномерно непрерывна.
Действительно,
Пусть
ε
– любое положительное число. Выберем
постоянную А
достаточ-но большой так, чтобы
Выберем
теперь такое малое h,
чтобы
Тогда
что и требова- лось доказать.
5)
,
т.к.
6)
Если x1,
… , xn
– независимые с.в., тогда
7)
C.в.
Y
не зависит от {Xi},
где
{Xi}
–
независимые, одина-ково распределенные
с.в., Y
– целочисленная с.в. с производящей
функ-цией φ(s),
g(t)
– характеристическая функция с.в. Xi
при
любом i.
Тогда
Действительно:
,
где 
возможные
значения с.в.
8)
Формула обращения:
где f(x)
– плотность рас-пределения с.в. Х;
g(t)
– характеристическая функция с.в. Х.
2.
Связь характеристической функции с
производящей функцией для целочисленной
с.в.
.
(2)
Задание. Зная производящие функции с.в., распределённых по законам: B(n,p), , G(p), cдG(p), Па(r,p), OB(r,p), найти соответствующие им характеристические функции, используя (2).
3. Нахождение характеристических функций, соответствующих задан-ным распределениям.
а)
X
~
R[a,b],
б)
X
~
N(0,1),
в)
X
~
N(a,
),
г)
X
~
E
д)
X
~
Коши.
Решение.
Для а) При X
~
R[–a,
a].
Задание. Пункты б) – д) решить самостоятельно.
4. Применение метода характеристических функций (МХФ) для ком-позиции.
Композицией законов распределения называется закон распределения сум-мы независимых с.в. с соответствующими законами распределения.
Задача 1.
X и Y – независимые с.в.; X ~ B(n1,p),Y ~ B(n2,p). Найти закон рас-пределения с.в. Z = X+Y.
Решение.
~
B(n2,p).
Аналогично найти композиции с.в. (МХФ) в случаях:
Задача
2. X
~
N(a1,
),
Y
~
N(a2,
).
Задача
3. X
~
Y
~
5. Связь характеристических функций с моментами МХ и DX.
Мξ = g′(0)/i,
Dξ = – g″(o) + ((g′(0))2.
Она
выводится из равенства: g(k)(0)
= ikM
(3)
(Если с.в. имеет абсолютный момент n-ого порядка, то g(t) дифферен-цируема k раз (k ≤ n)). Откуда при k=1 и 2.
Мξ
= g′(0)/i,
g″(o)+
((g′(0))2,
или при
Задание.
Получить последние формулы самостоятельно
для Мξ
и
по (3).
Метод характеристических функций (МХФ) состоит в использовании перечисленных свойств характеристической функции.