19. Триангуляционные сети

Триангуляция — сеть по возможности равносто­ронних треугольников, разбиваемых на поверхности Зем­ли; в этой сети намеряют одну или две стороны и все углы треугольников.

Для облегчения обработки результатов изме­рений приняты следующие стандартные обозначения (см. рис. 152,а):

b_l и Ь₂—измеренные базисные стороны;

a₁, а₂, ..., а_п — связующие стороны, общие для каждых двух смежных треугольников цепочки;

А₁ А₂, ..., А_п — связующие углы, расположенные против определяемых связующих сторон тре­угольников;

В₁, В₂, ..., В_п — связующие углы, расположенные против известных связующих сторон треугольников;

С₁, С₂ С_п — промежуточные углы, расположенные против промежуточных сторон треуголь­ников, являющихся внешними для тре­угольников данной цепочки.

При обработке результатов измерений в опорных се­тях; развитых по способу триангуляции, применяют те­орему синусов.

шагов, по звуковым сигналам.

20. Способы геометрического нивелирования

Геометрическое нивелирование выполняют двумя способами: вперед и из середины.

При нивелировании вперед для опреде­ления превышения h точки В над точкой А нивелир ус­танавливают окуляром над точкой А и измеряют над ней высоту визирной оси i. На точку В ставят верти­кально рейку. Направляют трубу нивелира на рейку и, приведя визирную ось в горизонтальное положение, определяют на рейке длину отрезка b между точкой В и визирным лучом трубы. Как видно из рисунка, пре­вышение

h = i-b. (108)

Высота точки в над уровенной поверхностью равна

H_b = H_a+h. (109)

Превышение считают положительным, если мест­ность при движении вперед повышается.

При нивелировании из середины на точки А и В ставят вертикально рейки, а в середине между ними — нивелир. После установки нивелира в рабочее положение трубу направляют на рейку, стоящую на задней точке А, визирную ось приводят в горизонтальное положение и делают отсчет а. Поворачивают трубу на точку В, приводят визирную ось в горизонтальное положение и делают отсчет Ь. Как видно из ри­сунка, превышение

h = a — b, (110)

Н_ь = Н_а + h.

Превышение при нивелировании вперед равно высо­те инструмента минус отсчет по рейке. Превышение при нивелировании из середины равно отсчету на заднюю рейку минус отсчет на переднюю рейку.

Визирную ось нивелира в горизонтальное положение устанавливают по уровню. Отсюда вытекает основное геометрическое условие, выполнение которого при работе с нивелиром обязательно: визирная ось трубы нивелира должна быть параллельна оси цилиндрического уровня. Это требование трудно выполнить точно, поэтому всегда имеют место незначительные погрешности.

21 Азимут и румб линии

Ориентироваться — значит определить свое место относительно точек или линий, положение которых из­вестно. Мерой ориентирования слу­жат углы —азимуты и румбы, считаемые от направле­ния меридиана. Различают меридианы истинные, или географические, и магнитные.

Азимутом направления называют угол, отсчитывае­мый по ходу часовой стрелки от северного направления меридиана, проходящего через данную точку, до напра­вления из этой точки на предмет. Азимуты изменяются от 0 до 360°.

Румбом направления называют угол между напра­влением на предмет и ближайшим к нему направлением меридиана, проходящего через данную точку. Румб обозначают направлением и величиной угла, например: СВ: 56°08. Величина румба изменяется от 0 до 90°.

По известному азимуту направления можно вычис­лить румб и обратно — по румбу можно вычислить ази­мут.

Угол δ между направлениями магнит­ного и истинного меридианов называют склонением маг­нитной стрелки.

22. Дирекционный угол

Если на рис. 31, а линия 1—4 прямая, то углы А, А₁... — ее азимуты в разных точках. Очевидно, что А<А₁<А₂... При вычислениях это вызовет значительные трудности, поэтому предложено искусственное построение, устраняющее указан­ный недостаток.

Через точки 2, 3... проводят пря­мые, параллельные меридиану од­ной из точек, например меридиану точки 1; получают углы α между вновь проведенными прямыми и данной прямой 1—4. Все угла а ра­вны между собой; их называют дирекционными углами. Дирекционные углы в отличие от азимутов от­считывают от какого-нибудь одного меридиана, который делит участок примерно пополам и проходит через один из геодезических пунктов. Этот ме­ридиан принято называть осевым, а дирекционные углы иногда называют осевыми азимутами.

При зональной системе координат осевым меридиа­ном служит центральный меридиан зоны. Таким обра-

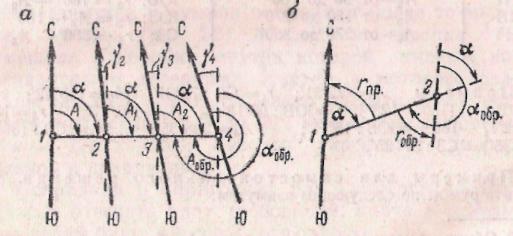
Рис. 31. Дирекционный угол

зом, дирекционным углом называют угол, сходный с азимутом, отсчитываемый от северного направления осевого меридиана зоны или меридиана, принятого за осевой, или от линии, параллельной осевому мери­диану.

Азимут обратного направления считают от меридиана конечной точки. В общем случае

А_обр=А_пр+180° (11)

20. Проекция Гаусса-Крюгера

Эта проекция относится к равноугольным поперечно-цилиндрически проекциям. Поверхность Земли проектируется на поверхность цилиндра, касающегося поверхности Земли по меридиану,

23. Разграфка и номенклатура листов карт

Номенклатурой называется система обозначений (нумераций) отдельных листов топографических карт (планов). В основу номен­клатуры топографических карт различных масштабов положена карта масштаба 1:1000000. Для получения одного листа карты этого масштаба весь земной шар делят (рис. 3.3) меридианами и парал­лелями на колонны и ряды (пояса). Меридианы проводят через каж­дые 6° на восток и запад, начиная от Гринвичского меридиана, а параллели — через каждые 4° к северу и югу, начиная от экватора. В результате этого размеры каждого листа такой карты будут рав­ны 4° по широте (ряды) и 6° по долготе (колонны). Номенклатура каждого листа карты 1:1000000 состоит из двух чисел: одно опре­деляет широтный ряд — пояс, другое — номер колонны

Разграфка листов всех карт более крупного масштаба строится каждый раз, исходя из деления на четыре части (средним меридиа­ном и средней параллелью) территории листа карты предыдущего более мелкого масштаба (например, для листов карты масштаба 1: 50 000, исходя из деления на четыре части территории листа карты масштаба 1: 100 000 его средним меридианом и средней параллелью). Поэтому номенклатура листа карты масштаба 1: 50 000 состоит из четырех знаков (три знака — номенклатура листа стотысячной карты, а четвертый номер листа — пятидесяти­тысячной карты в пределах этого стотысячного листа), карты ма­сштаба 1: 25 000 — из пяти, а карты масштаба 1: 10 000 — из шести знаков.

24 .Прямая задача на координаты

При составлении пла­нов ситуацию наносят от опорных точек и линий, их соединяющих. Поэто­му на бумагу сначала на­носят опорные точки по их координатам, которые

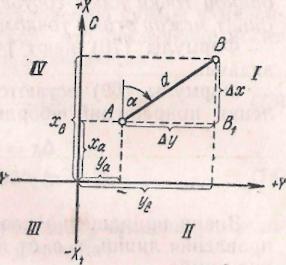
вычисляют в первую очередь, решая прямую задачу на координаты. Они состоит в том, что по известным координатам данной точки, а также дирекционному углу и горизонтальному проложеншо линии от этой точки до определяемой вычисляют координаты определяемой точ­ки. Например, известны координаты точки А (х_а и у_а.), Горизонтальное приложение d линии АВ, дирекционный угол α линии АВ.

25. . Уклон линии. График заложений

Уклоном линии iназывается отношение превышения hк ее за­ложению d. Уклон iявляется мерой крутизны ската.

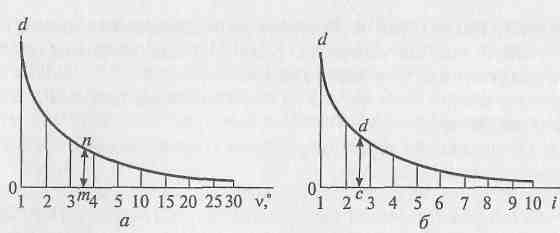
Рис. 3.11. Масштабы заложений:

а — по углам наклона; б — по уклонам

Так, например, при А = 1 м и / = l/d, откуда id= 1, т.е. произ­ведение уклона на заложение для данного плана — величина по­стоянная.

Обычно крутизну ската и уклоны определяют графически. Для этого на планах строят графики заложений. При построении тако­го графика величину заложения dопределяют по следующей фор­муле:

d=h/i, (3.2)

Следовательно,

d=hctgv.

26. Способы измерения площадей на планах и картах

На планах и картах площади можно определить аналитиче­ским, геометрическим и механическим способами.

Приборные погрешности обусловлены несовершенством технического средства измерений, погрешностями градуировки их шкал и т.д.

Личные погрешности зависят от несовершенства органов чувств, индивидуальных особенностей и квалификации испол­нителя.

Внешние погрешности порождаются непостоянством окружающей среды и связаны с изменением температуры, давления, влажностивоздуха и т.д.

Методические погрешности зависят от способа реализации процесса измерения, его теоретической основы, строгости учета ус­ловий измерения.

Каждая из перечисленных погрешностей вызывается целым рядом различных причин, которые могут возникать с неизбежностью (систематически), а могут — случайно. В связи с этим погрешности измерений по своим свойствам подразделяют на сис­тематические и случайные. Кроме того, результаты измерений могут содержать грубые ошибки.

Грубыми считают ошибки, существенно превышающие ожидаемые погрешности для данных условий измерений. Они являются результатом промахов (просчетов), возникающих вследствие невнимания или недостаточной квалификации исполнителя, незамеченных неисправностей технических средств измерений, на­рушения технологии, режима работы и других причин. Такие ошиб­ки выявляются повторными измерениями и исключаются из даль­нейшей обработки.

Если результат измерений не содержит грубых ошибок, то в нем одновременно присутствуют систематические и случайные погрешности.

Систематической погрешностью называют составляющую ее часть, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины. Системати­ческие погрешности могут сопутствовать каждому из компонентовусловий измерений, в связи с чем их обычно подразделяют на приборные, методические, личные и вызванные влиянием внеш­ней среды.

Приборные систематические погрешности нередко возникают вследствие неправильного выбора единиц измерения. Системати­ческие погрешности измерительного прибора устраняются его поверками и юстировками.

Если изучены природа возникновения или закономерности воздействия систематических погрешностей, то величину их влияния исключают из результатов измерений путем введения соот­ветствующих поправок. Несмотря на это, полностью исключить влияние систематических погрешностей невозможно, поэтому общая погрешность всегда в той или иной мере содержит систе­матическую составляющую. Однако существуют критерии, позво­ляющие пренебречь ее влиянием по сравнению со случайной со­ставляющей и тем самым упростить обработку результатов изме­рений и оценку их точности.

Когда результаты измерений практически не содержат систе­матических погрешностей, то их отклонение от истинного значе­ния в основном определяется величиной случайной составляю­щей.

Случайной погрешностью измерения называют составляющую часть общей погрешности, изменяющуюся случайным образом при повторных измерениях одной и той же величины. Такая изменчи­вость случайной составляющей обусловлена суммарным воздей­ствием на результат измерения множества неконтролируемых фак­торов (например, округление результата при отсчитывании пока­заний измерительного средства, случайные колебания температу­ры и др.).

Поэтому при проведении повторных измерений в одинаковых условиях каждая из многих возможных, но незначительных при­чин случайных изменений результатов может либо появиться, либо нет.

Характерно, что в серии измерений малые погрешности встре­чаются чаще, чем большие, и степень вероятности положитель­ных и отрицательных знаков погрешностей одинакова.

Отсюда следует вывод: 1) при бесконечно большом числе измерений арифметическое среднее из суммы случайных погреш­ностей равно нулю; 2) при конечном количестве измерений ариф­метическое среднее из суммы случайных погрешностей стремится к нулю.

В связи с этим рекомендуется измерение одной и той же вели­чины (угла, расстояния) производить неоднократно, как мини­мум, дважды.

Влияние случайных погрешностей избежать нельзя, но можно его уменьшить, определяя и учитывая их при использовании дан­ных измерений, применяя более совершенные приборы и техно­логические схемы.

При математической обработке геодезических измерений час­то используют термин «невязка». Невязка представляет собой ис­тинную погрешность функции (формулы, выражающей геомет­рическое соотношение в геодезическом построении) при подста­новке в нее вместо истинных значений аргументов их измеренных значений. Например, отклонение суммы измеренных