Предмет геодезия

Геодезия (с греч. землеразделение) — наука об измерениях, производимых для определения формы и размера Земли и изображе­ния ее поверхности на плоскости. Геодезию делят на высшую геодезию, и геодезию или топографию.

В задачу высшей геодезии входит определение фигу­ры и размеров Земли в целом и разработка методов особо точного определения координат точек земной поверх­ности.

Геодезия (топография) изучает измерения, необхо­димые для изображения небольших частей поверхности Земли на планах и топографических картах.

Разработкой методов составления географических карт на значительные территории занимается картогра­фия, используя при этом результаты геодезических из­мерений.

Аэрофотогеодезия.

Инженерная геодезия.

Геодезия при своем развитии опирается на достижения других наук и особенно математики, астрономии, физики, географии, инженерного искусства и др.

Математика вооружает геодезию методами анализа и обработки полученных результатов при измерениях.

Данные астрономических наблюдений геодезисты используют для ориентирования и определения координат исходных или контрольных точек.

Достижения физики для пользы геодезии неоценимы. Открытие закона тяготения явилось теоретическим основанием для определения формы Земли. Развитие оптики и электроники позволило сконструировать зрительную трубу, разработать дальномерные устройства и другие оптические и электронные измерительные приборы. Ряд законов, относящихся к физике жидких и газообразных тел, используют при геодезических измерениях.

Данные географии помогают правильно понять и изобразить на планах и картах ландшафт местности. Особое значение для геодезистов, гидротехников и мелиораторов имеет геоморфология — отрасль географии, изучающая строение рельефа земной поверхности.

Возникновение геодезии относится к глубокой древности. В государствах Ближнего Востока за несколько тысячелетий до нашей эры измеряли участки орошаемых земель и делили их по земледельцам. Строительство оросительных каналов в Египте требовало геодезических измерений на больших пространствах.

Развитию геодезии способствовало открытие в XV и XVI веках новых земель. Их надо было изобразить на бумаге, составить карты, а для этого прежде всего не­обходимо было провести геодезические измерения.

В России организованные съемки начали выполнять со времен Петра I, который посылал экспедиции в районы развития судоходства — на Волгу, Каспийское море, на Дон, Азовское море, на побережье Северного Ледовитого океана, на Сахалин, Камчатку и в другие части государства.

2, Форма и размеры Земли

Чтобы изобразить участок поверхности Земли на чертеже, надо знать форму поверхности и размеры Земли, которые определяются как общей фигурой Земли, так и характером рельефа данной местности.

Общую фигуру Земли образует основная уровенная поверхность. Поверхность, которая пересекает отвесные линии под прямым углом, называют уровенной. Теоретически такая поверхность может быть образована около любой заданной точки. Однако для практических целей принимают за основную ту из них, которая, совпадает с наибольшим числом точек земной поверхности. Поверхность океанов и морей в спокойном состоянии отвечает этим условиям. Поэтому спокойную поверхность океанов вместе с ее мысленным продолжением под материками приняли за основную уровенную поверхность. Идеальную фигуру, ограниченную основной уровенной поверхностью, называют геоидом и принимают за общую фигуру Земли.

В России за основную принята уровенная поверхность, проходящая через нуль Кронштадтского футштока (рейки для измерения уровня воды).

В уклонениях отвеса нет определенной закономерности, поэтому фигура геоида не выражена до сих пор математическими формулами. Ввиду этого при расчетах используют математически точную фигуру, близкую по форме к геоиду, — эллипсоид вращения, или сфероид. К настоящему времени размеры эллипсоида вычислены в нескольких странах. Вследствие недостаточного количества и качества данных, по которым вычислены эллипсоиды, их используют для топографо-геодезических целей лишь на ограниченных пространствах и называют референц-эллипсоидами.

На территории России с 1946 г. используют референц – эллипсоид (эллипсоид относимости), вычисленный к 1940 г. под руководством проф, Ф. Н. Красовского и проф. А.А. Изотова. Его размеры:

большая полуось а = 6 378 245 м

малая полуось b = 6 356 863 M

а — Ь сжатие α = -- - - = 1:298,3

а ,

В некоторые геодезических и картографических работах Землю приближенно принимают за шар с радиусом R = 6371 км.

3, Географические координаты

Одной из систем координат, с помощью которых можно определять положение точек на поверхности Земли, является система географических координат. Для этого используют линии меридианов и параллелей.

Меридианом данной точки называют линию пересечения поверхности Земли плоскостью, проходящей через ось вращения Земли и данную точку. Меридианы на сфероиде имеют форму эллипса. меридиан Гринвической астрономической обсерватории в Англии; его считают для всех стран мира начальным.

Параллелью данной точки называют линию пересече­ния поверхности Земли плоскостью, перпендикулярной оси вращения Земли и проходящей через данную точку. Параллели на сфероиде имеют форму окружности. Параллель , плоскость которой проходит через центр эллипсоида, на­зывают экватором.

Географическая система координат образуется пло­скостью экватора и плоскостью начального меридиана. Координатами в этой системе являются два угла — дол­гота и широта.

Долготой данной точки называют угол λ, образован­ный плоскостью начального меридиана и плоскостью ме­ридиана, проходящего через данную точку.

К востоку от начального меридиана до 180° долготы считают восточными к западу от начального меридиана до 180° — западными.

Широтой данной точки М называют угол φ, образо­ванный направлением отвесной линии в данной точке и плоскостью экватора.

Широты от экватора к северному полюсу называют северными, а от экватора к южному полюсу — южными. Они изменяются от 0 до 90°.

4. Прямоугольные плоские системы координат, используемые в геодезии

В геодезии используют систему координат Декарта с некоторыми изменениями: ось XX— вертикальная пря­мая, совпадающая с направлением одного из меридиа­нов; ось YY—горизонтальная (рис 3). Счет четвертей слева направо.

В России применяют две системы координат: зональ­ную и местную. При зональной системе поверхность зем­ного эллипсоида делят меридианами на 60 зон; по долго­те в каждой зоне 6°. Поверхность зоны по осо­бым правилам проектируют па плоскость и получают фигуру, на которой центральный — осевой меридиан зоны ось абсцисс XX, экватор — ось орди­нат YY. Чтобы избежать отрицательных знаков в орди­натах, начало ординат переносят на 500 000,0 м к запа­ду. Так как одинаково расположенные в зонах точки для разных зон имеют одинаковые координаты, то перед ординатами точек ставят номера зон, и ордината точки обозначится так: у = (номер зоны), 500 000 м +у^/, где у^/ - ордината точки А.

Например, ордината точки А выразится

У = (3), 500000 + 27 181,3 = 3 527 181,3.

Номера зон считают от Гринвичского меридиана к востоку. Чтобы координаты всех пунктов обоснования вычислять в единой системе, надо знать координаты хотя бы одного из них. Исходной точкой государственной системы координат в России принят центр Круглого зала Пулковской астрономической обсерватории.

Эта система носит название системы координат 1942 г.

Кроме зональной, используют системы координат от условного начала — местные произвольные системы координат. Зональная система позволяет составлять карты на значительные пространства, обеспечивает надежную связь между различными районами съемок. Местные системы создают разнобой в координатах, что затрудняет их связь между собой. Местные системы применяют в случаях, когда невозможно или трудно получить коорди­наты в зональной системе.

Принятую в России систему абсолютных высот назы­вают балтийской системой. В ней высоты считают от нуля Кронштадтского футштока.

5 Методы проектирования поверхности Земли на плоскость

Все предметы, находящиеся на поверхности Зем­ли, — леса, дороги, реки, сады, постройки, линии связи, осушительные и оросительные каналы и т. д. — в сово­купности называют ситуацией. Поверхность Земли ос­ложнена неровностями — холмами, западинами, оврага­ми, хребтами, увалами и т. д.

Сочетание различных неровностей земной поверхно­сти называют рельефом.

Чтобы составить план или карту участка местности, надо выполнить две операции: сначала спроектировать рельеф и ситуацию местности на общую фигуру Земли, а затем по разработанным математическим правилам, которые называют картографическими проекциями, об­щую фигуру вместе с изобразившимися на ней элементами поверхности Земли спроектировать на плоскость.

В случае значительной площади участка его поверхность нормалями проектируют на эллипсоид как общую фигуру Земли. Поскольку эллипсоид — мате­матически известная фигура, для него разработан ряд картографических проекций, позволяющих фигуру abed на сфероиде с учетом определенных требований спроек­тировать на плоскость; уменьшив a'b'c'd', получают карту.

Небольшие участки, размер которых позволяет принимать поверхность общей фигуры за плоскость, проек­тируют, отвесными линиями на поверхность геоида. Поскольку в этом случае отвесные линии практически параллельны и пересекают плоскую по­верхность геоида под прямым углом, образуется горизонтальная проекция, или горизонтальное проложение участка местности.

Расстояние по отвесной линии Аа = Н_а называют высотой точки А над уровенной поверхностью. Если поверхность Р совпадает с основной уровенной поверхно­стью, расстояние Н_а называют абсолютной высотой (аб­солютной отметкой, альтитудой). Расстояние по отвесной линии от точки А до любой другой уроненной поверх­ности называют условной высотой.

Разность высот двух точек С'С называют превыше­нием h.

6, Масштабы

Горизонтальные проложения линий местности на чертежах изображают в некотором уменьшении. Это уменьшение или отношение длины отрезка линии на чертеже к длине горизонтального проложения соответствующего отрезка линии местности называют масштабом.

Масштабы, выражаемые числовыми величинами, называют численными; масштабы, изображаемые графиками, называют графическими.

Численный масштаб выражают или дробью, например 1:1000, или именованным соотношением — 1 см на чертеже соответствует 10 м на местности.

Графические масштабы бывают линейные и поперечные. Линейный масштаб, изображаемый на планах и картах, как правило, дополняют численным масштабом. Он служит лишь для грубых измерений, так как доли наименьшего деления левого отрезка—основа­ния - определяют на глаз.

Для повышения точности измерения отрезков линий на чертежах или перенесения длин измеренных отрезков на чертежи применяют поперечный масштаб, который строят в виде графика. Расстояние между вертикальными прямыми графика называют основанием масштаба, по стандарту оно может быть равно 10, 20, 40, 50 мм. Высота графика 20—30 мм. Вертикальные линии масштаба делят на п частей и через их концы проводят прямые горизонтальные линии, параллельные основанию. Крайнее основание делят на m малых частей, через концы которых проводят наклонные прямые — трансверсали. Указанным приемом построения поперечного масштаба получают наименьшее деление масштаба, величина которого

ab = АВ: n

Если основание равно 20 мм, m=n = 10, то

ab = 20:mn = 0,2'мм;

при основании 40 мм ab= 0,4 мм и т. д.

Опытом, установлено, что отрезок линии на бумаге абсолютно точно отложить нельзя, появляются отклоне­ния, среднюю величину которых, близкую к 0,1 мм, и на­зывают графической точностью нанесения отрезка на бумагу. Предельная допустимая ошибка и длине нанесенного отрезка на бумагу не должна превышать 0,2 мм — величины осторожного укола иглы циркуля.

При разных численных масштабах графической точ­ности соответствуют разные длины отрезков местности. Например, при масштабе 1 : 1000 одной десятой милли­метра на плане соответствует 0,1 м на местности, при масштабе 1 : 10 000—1 м.

Эти отрезки показывают, какой наименьшей величи­ны изгибы четких контуров надо измерять, чтобы не до­пускать ошибку при съемках. Поэтому отрезок на мест­ности, соответствующий одной десятой миллиметра на плане и данном масштабе, называют точностью мас­штаба.

7, План, карта, профиль

Планом называют чертеж, на котором в уменьшенном и подобном виде изображена горизонтальная проекция небольшого участка земной поверхности.

Как уже указывалось, при съемках небольших участ­ков за общую фигуру Земли принимают геоид, а его по­верхность считают плоской. Величину участка, изобра­жаемого планом, ограничивают такими размерами, за пределами которых ошибка за общую кривизну Земли начнет оказывать заметное влияние на точность состав­ления плана и вместе с неизбежными ошибками полевых измерений и нанесения точек на бумагу будет выходить за пределы допусков, определяемых инструкциями.

Принято считать, что план можно составлять на тер­риторию, не превышающую площади круга радиусом 10 км.

Если на плане изображена только ситуация, его на­зывают контурным. Если кроме ситуации на план нанесен и рельеф, такой план называют топогра­фическим. Масштаб плана во всех его точках одинаковый.

Картой называют чертеж, на котором по определен­ным математическим правилам с учетом кривизны об­щей фигуры Земли может быть изображена поверхность всей Земли или любой ее части в обобщенном и умень­шенном виде.

Составляемые карты можно различать по содержа­нию: сельскохозяйственные, мелиоративные, экономичес­кие и т. д. – это так называемые специальные карты, на них показывают контуры и специальную нагрузку. Кар­ты, на которых кроме контуров ситуации изображен рельеф земной поверхности называют общегеографическими. Такие карты, соствавляемые в крупных масштабах (от 1:100 000 и , крупнее, т. е. до 1:10 000, 1:5000), называют топографическими , они служат основой для составления всех других карт. Масштаб во всех точках карты различен.

Для обозначения предметов на карте разработаны условные знаки. Употребление одинаковых условных знаков обязательно для всех ведомств.

Профиль— чертеж, на котором изображен верти­кальный разрез поверхности земли по заданному на­правлению. Сам разрез также называют профилем.

8, Организация и виды геодезических работ

Геодезические работы организуют по общему правилу перехода от общего к частному.

Прежде всего создают геодезическое обоснование, или опорную геодезическую сеть, под которой понимают систему обозначенных на местности точек с вычисленными для них координатами.

Опорные сети бывают плановые и высотные. Для точек планового обоснования обязательно более точное определение координат х,у; их высоту определяют не всегда с высокой точностью. Для точек высотного обоснования обязательно более точное определение абсолютных высот; их координаты х,у иногда определяют приблизительно.

По точности опорные сети делят на несколько классов. Государственные геодезические сети состоят из четырех классов: первый класс наиболее точный.

Точки, с которых производят съемку, называют съемочными.

Опираясь на точки съемочного обоснования, проводят съемку, результаты которой служат для составления планов или карт. Различают съемку контурную, или горизонтальную, по данным которой составляют контурные планы, и топографическую, по результатам которой составляют топографические планы и карты.

Каждый из указанных видов работ складывается из полевых измерительных и камеральных вычислительных и составительских работ.

9. Понятие о картографических проекциях

Математически выраженные правила, по которым поверхность Земли проектируют на плоскость, называют картографическими проекциями. Ими устанавливается строгое соблюдение масштабов в каждой точке карты.

По характеру искажений, возникающих при изобра­жении поверхности Земли на плоскости, картографиче­ские проекции делят на равноугольные, равновеликие и произвольные.

К равноугольным, или конформным, проекциям отно­сят такие, при которых бесконечно малые фигуры изоб­ражаются без искажений, т. е. в каждой точке круг изо­бразится кругом

μ_а =m=n,

а масштаб площади всюду различен, т. е. р=mп ≠const.

Ввиду того что при переходе от одной точки к другой масштабы изменяются, для фигур конечных размеров подобие на картах не сохраняется, хотя углы остаются без искажений.

К равновеликим, или эквивалентным, проекциям относят такие, при которых для участков любой величины сохраняется масштаб площади, т. е. в любом месте карты

р = mn = const.

К произвольным относят проекции, при которых ни равноугольность, ни равновеликость не соблюдены.

В зависимости от того, какая поверхность бралась за промежуточную, картографические проекции делят на цилиндрические, конические, перспективные, многогран­ные и др.

Многогранную проекцию применяют при составлении многолистных карт. Картографируемую поверхность разбивают на сфероидические трапеции. Каждую такую трапецию по заранее выработанным правилам проектируют на плоскость; в результате образуется как бы многогранник. При этом переходной поверхностью может быть цилиндр, конус и др.

10. Рельеф , виды рельефа.

Физическая поверхность земли неровная, на ней име­ются возвышения, углубления и сравнительно плоские участки. Совокупность этих неровностей определяет рельеф земной поверхности. Различают рельеф горный, холмистый, равнинный.

Из всего многообразия отдельных форм неровностей земной поверхности выделяют основные формы рельефа: гору, котловину, хребет, лощину, седловину и др.

Гора— куполообразное или конусообразное возвыше­ние с ясно выраженным основанием — подошвой. Котловина — замкнутое чашеобразное углубление. Хребет — вытянутая возвышенность. Линию, идущую вдоль хребта и соединяющую наиболее возвышенные его точки, называют водораздельной линией.

В результате действия текущей воды часто вдоль склонов образуются промоины, которые впоследствии могут превратиться в oвpaги.

Седловина — небольшая площадка, к которой с двух противоположных сторон подходят возвышенности, а в две другие стороны спускаются лощины.

11. Способы Изображение рельефа на планах и картах

Для изображения рельефа местности на топографических картах и планах изображают с помощью надписей высот и горизонталями. На кapтах более мелких масштабов для большей наглядности при изображении рельефа применяют отмывку и штриховку.

Горизонталями называют линии земной поверхности, соединяющие точки с одинаковыми высотами.

Рассечем небольшую часть физической земной по­верхности горизонтальными равноотстоящими одна от другой плоскостями, параллельными уроненной поверхно­сти. Образующиеся в peзультате этого следы сечения на земной поверхности и есть горизонтали. Paccтояния h по высоте между секущими плоскостями или одной горизонтали от другой называют высотой сечения рельефа.

При одинаковой высоте сечения рельефа расстояния на плане между горизонталями больше у по­логого склона и меньше у крутого; эти расстояния назы­вают заложением.

Из определения горизонталей вытекают следующие их свойства:

все точки, лежащие на одной горизонтали, имеют оди­наковую высоту на местности;

горизонтали — непрерывные линии, своим начертанием обозначают формы рельефа местности;

горизонтали не пересекаются между собой; в местах обрыва они на плане сливаются;

на склонах одинаковой крутизны заложения одина­ковы;

по величине заложения можно определять крутизну склона.

Если высота сечения рельефа h, заложение d, то для любого отрезка на поверхности земли можно определить угол его наклона v, или уклон i, т. е.

h/d=tgv=i(3)

12. Способы съемки контуров ситуации (подробностей)

Чтобы элементы ситуации изобразить на плане в их подобном виде, на местности, намечают и снимают ха­рактерные точки на их контурах (границах) — главным образом точки поворота границ.

Способ обхода применяют для съемки вытяну­тых объектов (дорог, каналов) или обособленных эле­ментов ситуации (лес, болото). Криволинейную границу участка разбивают на отрезки 1—2, 2—3 ... (рис. 27,а), которые для данного масштаба съемки можно считать прямыми. Отклонения фактической границы от съемоч­ных линий допускают не более двойной точности мас­штаба съемки. Например, точность масштаба 1:5000 равна 0,1 ммХ5000=0,5 м, следовательно, фактические границы от прямых d₁, d₂ ... могут отклоняться не бо­лее 1 м.

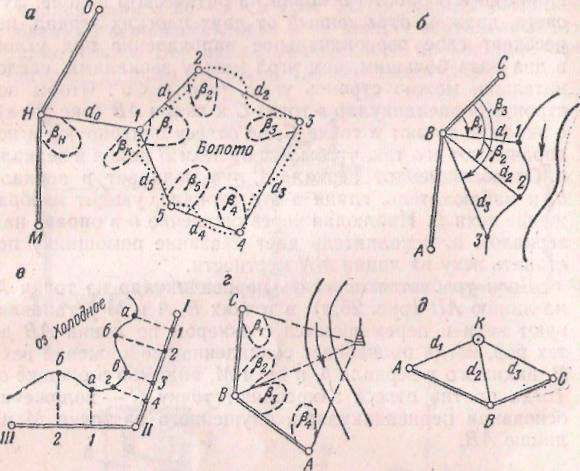
Рис. 27. Способы съемки ситуации:

я —способ обхода; б — полярный способ; в —способ перпендикуляров; г — спо­соб угловых засечек; д — способ линейных засечек

Концы намеченных отрезков закрепляют кольями или столбами и получают полигон 1—2—3 ... Линии этого полигона измеряют лентой или дальномером, а горизонтальные углы р₁, р₂ , … — угломерным ин­струментом. Вместо измерения горизонтальных углов допускают измерение прямых и обратных магнитных азимутов или румбов линий 1—2, 2—3 буссолью.

Полигон обязательно привязывают к линиям съе­мочной сети путем измерения примычных углов β_н и β_к и длины линии d_o.

Способ полярных координат.

Способ перпен­дикуляров. Приме­няют при съемке вытяну­тых объектов, например, каналов, дорог, а также при городских съемках.

Перпендикуля­ры строят длиной до 20 м — на глаз: до 100 м — эке­ром; свыше 100 м — теодолитом.

Способ угловых засечек. Применяют для съемки отдельно стоящих деревьев, столбов, башен, вы­шек и др., не доступных для линейных измерений.

Способ линейных засечек применяют сравнительно редко, главным образом при отсутствии угло­мерных приборов, при коротких базисных линиях. При этом способе как минимум от трех опорных точек, на­пример, А, В, С (рис. 27, д) измеряют расстояния до сни­маемой точки d₁, d₂ и d₃.

6. Способ триангуляции применяют для точного оп­ределения сравнительно небольшого количества контур­ных точек.

Триангуляция состоит из нескольких треугольников, в которых измеряют одну или две стороны и все углы.

8. Съемка контуров способом аэрофотосъемки. В ре­зультате фотографирования местности с самолета кон­туры получают непосредственно на аэрофотоснимке, где они изображаются весьма наглядно. Однако линии на аэрофотоснимке разномасштабные, а потому их исполь­зуют по особым правилам.

Абрис. Грани­цы участка и внутреннюю ситуацию изображают в про­извольном масштабе, на нем записывают результаты измерений углов и длин линий, названия объектов и уро­чищ. Ориентируют абрис по странам света на глаз, для чего при его составлении следует встать лицом к северу.

Все записи и изображения на абрисе должны быть четкими и разборчивыми, для чего пользуются линейкой и угольником. Для участков бо льших размеров абрис составляют по частям на нескольких страницах.