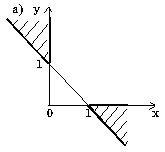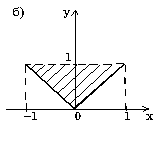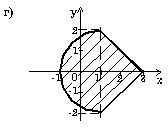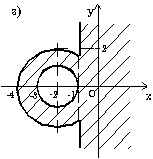- •Лабораторная работа №2. Разветвляющиеся алгоритмы.
- •Лабораторная работа № 3 Организация циклов “пока” и “До”
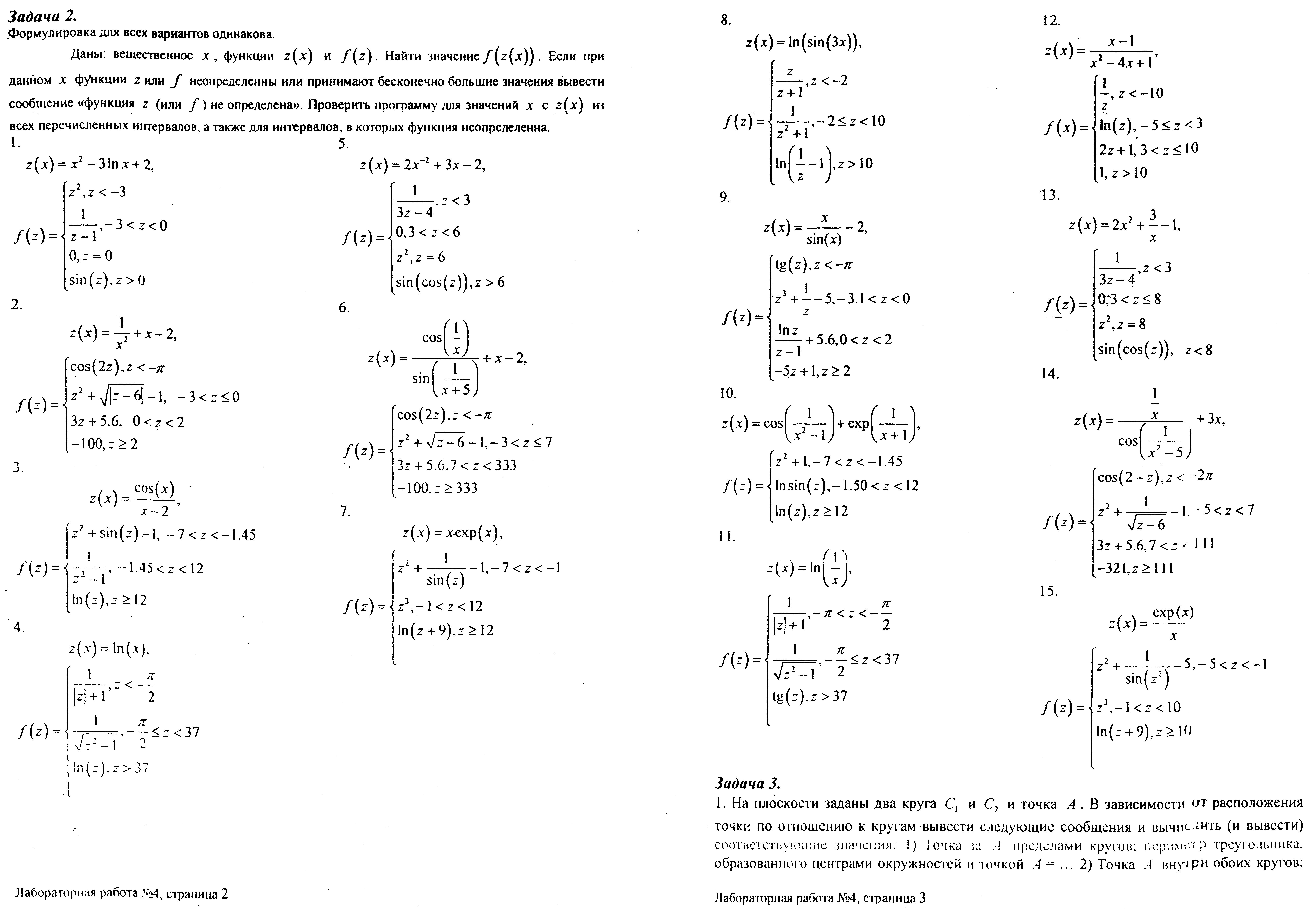
- •Лабораторная работа № 4. Процедуры и функции.
- •А) с использованием процедур б) с использованием функций
- •Лабораторная работа №5. Одномерные массивы
- •Лабораторная работа №6. Двумерные массивы.
- •Лабораторная работа №8. Множества.
- •Лабораторная работа № 9 Комбинированный тип данных (записи)
- •Лабораторная работа №10. Файлы
- •Лабораторная работа №11. Задачи на графические построения.
Лабораторные работы по
ПРЗ на ЭВМ
для факультета физмат
Шагиевой Ф.И.
Линейные алгоритмы.
Разветвляющиеся алгоритмы.
Организация циклов «Пока» и «До»
Процедуры и функции
Одномерные массивы 3 языка
Двумерные массивы 3 языка
Строковый и множественный типы данных 2 язык QB,P
Множества P
Комбинированный тип данных(записи) P
Файлы P
Графика P
Разветвляющиеся алгоритмы. 6
Организация циклов “ПОКА” и “До” 10
Процедуры и функции. 12
Одномерные массивы 14
Строковый и множественный типы данных 20
Комбинированный тип данных (записи) 24
ФАЙЛЫ 28
Выполнить задачи на 3х языках программирования:
Кумир (ШАЯ), FreeBasic, Pascal ABC
Лабораторная работа №1.
Линейные алгоритмы.
Выполнить на трех языках программирования: Паскаль, Бейсик, ШАЯ.
Задание I.
Вычислить выражение:

Задание II.
Составьте программу для вычисления величины работы, совершенной при равномерном подъеме груза массой М кг на высоту H м. Ускорение свободного падения описать как константу G = 9,81.
Составьте программу для вычисления давления столба жидкости плотностью R высотой H на дно сосуда.
Составьте программу для вычисления выталкивающей силы, действующей на тело объемом V, наполовину погруженное в жидкость плотностью R.
Составьте программу для вычисления количества теплоты по формуле Q = cm(t2-t1).
Составьте программу для вычисления количества теплоты, полученной при сгорании М г керосина, если его теплота сгорания q.
Составьте программу для вычисления величины силы тока на участке электрической цепи сопротивлением R Ом при напряжении U В.
Составьте программу для вычисления напряжения на каждом из последовательно соединенных участков электрической цепи сопротивлением R1, R2, R3 Ом если сила тока при напряжении U В составляет 1 А.
Составьте программу для вычисления значения силы тока I на участке, состоящем из двух параллельно соединенных резисторов сопротивлением R1 и R2, если напряжение на концах этого участка равно U.
Задание III.
Расстояние между домами, в которых живут Петя и Коля, 1200 м. Однажды они вышли каждый из своего дома и направились навстречу друг другу. Когда Петя прошел А метров, они встретились. Во сколько раз расстояние, которое прошел Коля больше расстояния, которое прошел Петя?
От станции до озера S км. Туристы, направляясь от станции к озеру, полтора часа шли пешком со скоростью А км, а затем сели на попутную машину, которая ехала со скоростью В км/ч. За какое время туристы добрались до озера?
Из 18 т железной руды выплавляют 10 т железа. Сколько железа выплавят из А т руды?
Чтобы заварить 1,5 л чая, нужно 30 г сухого чая. Чайник вмещает В л. Сколько нужно сухого чая для заварки?
В школьном коридоре длиной 56 м нужно выкрасить пол. Выкрасив часть коридора длиной 22 м, израсходовали А кг краски. Сколько еще нужно краски, докрасить коридор?
Чтобы сварить 4 порции пшенной каши, нужно взять 220 г пшена, 1 л молока и 30 г сахара. Сколько потребуется этих продуктов, чтобы сварить N порций каши?
Универмаг в ноябре продал товаров на А млн. р., что на 15% больше, чем в октябре. На какую сумму были проданы товары в октябре?
Сахарная свекла содержит 14% сахара. С 1 га собирают 30 т сахарной свеклы. сколько гектаров надо засеять сахарной свеклой, чтобы получить В т сахара?
Задание IV.
Даны два числа. Найти среднее арифметическое кубов этих чисел и среднее геометрическое модулей этих чисел.
Вычислить расстояние между двумя точками с данными координатами x1, y1 и x2, y2.
По двум данным катетам найти гипотенузу и площадь прямоугольного треугольника.
Даны числа x и y. Вычислить их сумму, разность и произведение.
Смешано v1 литров воды температуры t1 с v2 литрами воды температуры t2. Вычислить объем и температуру образовавшейся смеси.
Составьте программу для вычисления необходимой массы соли и воды для приготовления раствора массой m г с массовой долей w %.
Автомобиль проехал три участка пути разной длины с разными скоростями. Найти среднюю скорость автомобиля.
Даны катеты прямоугольного треугольника. Найти его гипотенузу и площадь.
Лабораторная работа №2. Разветвляющиеся алгоритмы.
Выполнить на трех языках программирования: Паскаль, Бейсик, ШАЯ.
Задание I.
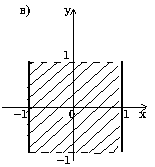
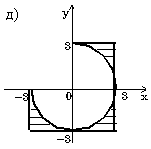
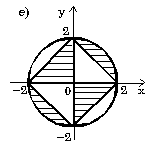
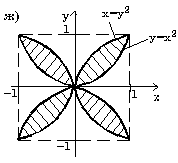
Проверить принадлежит ли заштрихованной области точка с координатами (x, y).
|
|
|
|
|
|
|
|
|
Задание II.
Задание III.
Определите, имеется ли среди заданных целых чисел A, B, C хотя бы одно четное.
Определите, пройдет ли кирпич с ребрами a, b, c в прямоугольное отверстие со сторонами x и y. Просовывать кирпич в отверстие разрешается только так, чтобы каждое из его ребер было параллельно или перпендикулярно каждой из сторон отверстия.
Выберите наибольшее из трех заданных чисел.
Решите квадратное уравнение
 .
.Даны три числа. Выведите те из них, которые принадлежат заданному отрезку [a, b].
Заданы площади круга и квадрата. Определите, поместится ли круг в квадрате.
Заданы площади круга и квадрата. Определите, поместится ли квадрат в круг.
Проверьте, можно ли построить треугольник из отрезков с длинами x, y, z и, если можно, то какой – остроугольный, прямоугольный или тупоугольный.
Задание IV.
Дан номер года. Найти число дней в этом году. Указание. В современном (григорианском) календаре каждый год, номер которого делится на 4, является високосным, за исключением тех, которые делятся на 100 и не делится на 400. Например, 1900 год - не високосный, 2000 год - високосный.
Составьте программу, определяющую, входит ли введенная вами цифра в десятичную запись введенного вами трехзначного числа.
Даны координаты центров двух окружностей (X1,Y1) и (X2,Y2), а также их радиусы R1 и R2 (R1>R2). Определить взаимное расположение окружностей.
На плоскости заданы точки M1(X1,Y1), M2(X2,Y2), N1(X1,Y1), N2(X2,Y2). Проверить, являются ли параллельными прямые M1M2 и N1N2. Если прямые пересекаются, то найти их точку пересечения.
Найти координаты точек пересечения прямой y=kx+b и окружности радиуса R с центром в начале координат. Определить, сколько точек пересечения находится во второй координатной четверти.
Составьте программу, которая по введенному вами k – числу грибов, печатает фразу «Мы нашли в лесу k грибов, причем согласовывает окончание слова «гриб» с числом k.
Даны три действительных числа a, b, c. Определить, являются ли они последовательными членами арифметической последовательности.
Составьте программу, которая для целого числа k (от 1 до 99), введенного вами, напечатает фразу «Мне k лет», при этом в нужных случаях слово «лет» заменяя на слово «год» или «года».
Лабораторная работа № 3 Организация циклов “пока” и “До”
Задание 1.
Используя
два вида операторов цикла составить
программы табулирования функции
![]() на отрезке [a,
b]
с шагом
на отрезке [a,
b]
с шагом
![]() где m
– заданное число.
где m
– заданное число.
Вариант |
Функция |
a |
b |
m |
1 |
xsin(x) |
0 |
3 |
10 |
2 |
cos (1/x) |
/4 |
4/ |
20 |
3 |
sin(x2) |
/6 |
2/3 |
10 |
4 |
cos(x2) |
/3 |
3/2 |
15 |
5 |
sin(x)+tg(x) |
0 |
/4 |
20 |
6 |
cos(x)+ctg(x) |
/4 |
/2 |
10 |
7 |
ctg(x/3)+sin(x) |
/4 |
/2 |
10 |
8 |
x2+sin(x) |
-2 |
2 |
20 |
Задание 2.
Используя операторы цикла с предусловием и постусловием, найти сумму ряда с точностью =10-3 и =10-4, общий член которого an (см.вариант). Определить, сколько членов ряда просуммировано.
Вариант |
an |
Вариант |
an |
1 |
(2n-1)/2n |
5 |
2n/n! |
2 |
n!/(2n)! |
6 |
(-1)n32n/(2n)! |
3 |
3nn!/(3n)! |
7 |
52n+1/(2n+1)! |
4 |
n2/3n |
8 |
(n-3)/(2n+1)! |
Указание: 1. Считать , что точность достигнута, если abs(an)<.
2. Для получения следующего члена ряда использовать рекуррентную формулу, выражающую an+1 через an. Для этого вычислить их отношение.
Например,
![]()
![]() Откуда,
Откуда,
![]() .
.
Задание 3
Задано целое А>25. Найдите наименьшее целое неотрицательное k, при котором 5k > А.
Числа Фибоначчи F определяются по формулам F0=F1=1, Fi=Fi-1+Fi-2 при i= 2, 3, ... Найдите первое из чисел Фибоначчи, которое превосходит заданное число М (М>0).
Дано натуральное число N. Выясните, сколько цифр оно содержит.
Даны два натуральных числа М и N - числитель и знаменатель дроби M/N. Требуется сократить дробь, насколько это возможно.
Дано натуральное число N. Получите его запись в двоичной, восьмеричной и шестнадцатеричной системах счисления.
Заданное натуральное число М представьте в виде суммы квадратов двух неравных натуральных чисел. В случае, если это невозможно, выведите соответствующее сообщение.
Вычислить sinn x
Вычислить S=N+(N-1)+…+3+2+1
Задание 4. (“Для” и “n раз”)
Составить программу вычисления таблицы значений функции одной переменной z=f(x) при х, изменяющемся на отрезке [a, b] с шагом Hx.
Таблицу вывести на экран в прямоугольной форме.
Варианты задания:
вариант |
z |
a |
b |
Hx |
1 2 3 4 5 6 7 8 |
5x+6 6x-5 x*x+1 3x+1 x2+3x x3+5 4x-x2 x/2+5 |
-9 -5 -13 -3 -15 -11 -5 0 |
15 16 3 15 20 10 16 21 |
4 3 2 2 5 3 3 2 |