3.3 Приложения определенного интеграла к вычислению площадей плоских фигур

Найдем площадь S криволинейной трапеции, ограниченной кривой y=f(x), осью Ох и двумя прямыми х = а и х = в, где а≤ х≤ в, f(x)≥0 (рис.5)

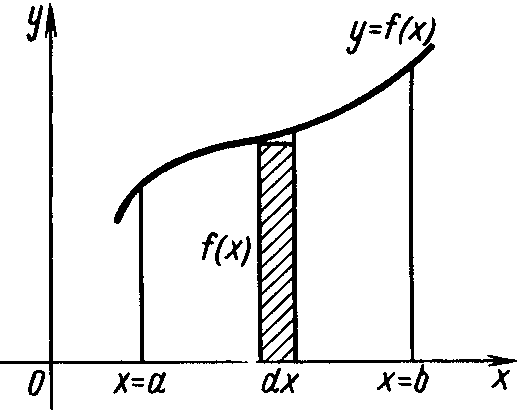
Рисунок 5 - Криволинейная трапеция

Так как дифференциал переменной площади S есть площадь прямоугольника с основанием dx и высотой f(x), т.е. dS=f(x)dx, то, интегрируя это равенство в пределах от а до в, получим

Если криволинейная трапеция прилегает к оси Oy так, что c≤y≤d, x=φ(y)≥0 (рис.6),

Рисунок 6 - Криволинейная трапеция прилегает к оси Oy

то дифференциал переменной площади S равен dS=f(y)dy, откуда

(5)

В том случае, когда криволинейная трапеция, ограниченная кривой y=f(x), осью Ох и прямыми х = а и х = в, лежит под осью Ох (рис.7),

Рисунок 7 - Криволинейная трапеция лежит под осью Ох

площадь находится по формуле

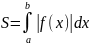(6)

Если фигура, ограниченная кривой y=f(x), осью Ох и прямыми х = а и х = в, расположена по обе стороны от оси Ох (рис.8),

Рисунок 8 - Криволинейная трапеция расположена по обе стороны от оси Ох

то

(7)

Пусть, наконец, фигура ограничена двумя пересекающимися кривыми y=f₁(x) и y=f₂(x) и прямыми х = а и х = в, где a≤x≤b и f₁(x)≤ f₂(x) (рис.9).

Рисунок 9 - Фигура ограничена двумя пересекающимися кривыми y=f₁(x) и y=f₂(x)

Тогда ее площадь находится по формуле

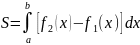(8)

Раздел 4. Основы дискретной математики

4.1 Множества. Операции над множествами. Бинарные

отношения

Множество – совокупность элементов, обладающих каким-то одним общим свойством.

Предметы, составляющие множество, называются его элементами. Говорят, что они принадлежат множеству. Символически это записывается так: а∈А.

Множества будем обозначать загл. буквами (А,В,С), а элементы – маленькими (а,в,с). Запись а∉А означает, что элемент а не принадлежит множеству А.

Пример 1. Пусть А – множество делителей числа 12. Тогда 2 ∈А, а 5 ∉А.

Если каждому элементу множества можно присвоить номер и этот номер не повторяется, то такое множество называется счетным или конечным.

Если такого номера для каждого элемента не существует, то такое множество называется бесконечным.

Бесконечное множество часто называют континуумом (например: совокупность точек на плоскости).

Если можно пересчитать все число элементов в счетном множестве, то эта сумма называется мощностью множества.

2. Множества можно задать следующим образом.

• Перечислением всех входящих в него объектов. - множество десятичных цифр.

• Описанием свойств, которыми должны обладать элементы множества. Например, множество четных чисел, меньших 10, можно задать в след. виде: М= или , причем справа от наклонной черты указано свойство элементов этого множества. Этот способ называется аналитическим.

Любую часть множества А, выбранную по определенному признаку, называют подмножеством, и обычно обозначают буквой со штрихом, т.е. :

, где ⊂ - символ включения.

Множество, не содержащее ни одного элемента, называют пустым и обозначают ∅.

Свойства счетных множеств

1. Всякое подмножество счетного множества конечно или счетно

Подмножеством множества А называется множество А` все элементы которого принадлежат множеству А

Пример:

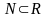
2. Сумма конечного или счетного числа конечных или счетных множеств есть конечное или счетное множество.

3. Множество всех рациональных чисел счетно.

4. Алфавитом называется любое непустое множество.

Элементы множества под названием АЛФАВИТ называют буквами (символами).

Символом в данном алфавите любая конечная последова­тель­ность букв.

Для каждого множества А существуют множества, элементами которого являются только все его подмножества.

Такое подмножество называют семейством множеств А или булеаном. (обозначается В(А))

Основные операции над множествами

1. Включение

Множество А входит (включено) в множество В, или А является подмножеством В.

Если всякий объект, обладающий свойством , также обладает свойством , то говорят, что свойство включает свойство , т.е.

2. Объединение

Сумма множеств А и В есть множество С, включающее в себя все элементы множество А и В.

Объект входит во множество если он входит во множество А или во множество В.

3. Пересечение

Пересечением множество А и В называется новое множество С. Элементы множества С принадлежат множеству А (обладают его свойствами) и множеству В (обладают его свойствами).

4. Разность

Разность множеств А и В есть множество С, элементы которого обладают свойствами множества А и не обладают свойствами множества В или принадлежат множеству А и не принадлежат множеству В.

5. Дополнение

Если имеется некоторое универсальное множество (универсум) U и все рассматриваемые множества есть его подмножества, то дополнением называется такое множество, элементы которого не входят в А, но принадлежат U.

Таблица 4 - Связь между логическими операциями и операциями над множествами.

Отрицание	Дополнение
Конъюнкция	Пересечение
Дизъюнкция	Объединение
Импликация	Разность

Будем называть вектором (кортежем) упорядоченный набор элементов и обозначать его 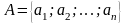, заметим, что в отличие от множества, элементы в векторе могут повторяться. Эти элементы называются координатами или проекциями.

Количество элементов в векторе называется его длиной, если в векторе 2 элемента, то - пара , если n элементов, то - n-ка.