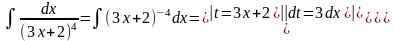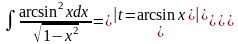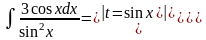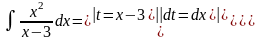- •Братский целлюлозно-бумажный колледж
- •Методические указания к практическим работам
- •Введение
- •Раздел 1 Элементы линейной алгебры
- •1.1 Матрицы и определители. Операции над матрицами. Определители, миноры, алгебраические дополнения. Обратная матрица
- •1.2 Решение систем линейных уравнений
- •Раздел 2. Основы дифференциального исчисления
- •2.1 Понятие производной. Правила и формулы дифференцирования. Производная сложной функции
- •2.2 Применение производной к исследованию функций и построению графиков
- •Раздел 3. Основы интегрального исчисления
- •3.1 Первообразная функции. Неопределенный интеграл и его
- •3.2 Определенный интеграл и его свойства. Формула Ньютона – Лейбница. Вычисление определенных интегралов
- •3.3 Приложения определенного интеграла к вычислению площадей плоских фигур
- •Раздел 4. Основы дискретной математики
- •4.1 Множества. Операции над множествами. Бинарные
- •5. (Диаграммы Эйлера - Венна)
- •Раздел 5. Основы теории вероятностей и математической статистики
- •5.1 Элементы комбинаторики: размещения, перестановки,
- •5.3 События и их виды. Операции над событиями
- •5.5 Вычисление вероятностей простых и сложных событий
- •5.7 Дискретные случайные величины ( дсв). Законы распределения дсв. Числовые характеристики дсв
- •Раздел 6. Основы теории комплексных чисел
- •6.1 Определение комплексного числа в алгебраической форме, действия с комплексными числами
- •6.2 Геометрическая интерпретация комплексных чисел. Решение алгебраических уравнений Геометрическое изображение комплексных чисел
- •Модуль и аргумент комплексного числа
- •Список использованных источников
Раздел 3. Основы интегрального исчисления
3.1 Первообразная функции. Неопределенный интеграл и его
свойства. Основные табличные интегралы. Интегрирование функций
Определение:
Функция
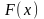 называется
первообразной
для функции
называется
первообразной
для функции
 на
промежутке
на
промежутке
 ,
если в любой точке этого промежутка её
производная равна
:
,
если в любой точке этого промежутка её
производная равна
:

Отыскание первообразной функции по заданной её производной или по дифференциалу есть действие, обратное дифференцированию – интегрирование.
Пример:
Дана функция
.
Её первообразная
 ,
т.к.
,
т.к.
 .
Очевидно, что первообразными будут
также любые функции
.
Очевидно, что первообразными будут
также любые функции
 ,
т.к.
,
т.к.
 и
и

 .
.
Совокупность всех
первообразных для функции
или для дифференциала
 называется неопределенным
интегралом
и обозначается:
называется неопределенным
интегралом
и обозначается:
 ,
(4)
,
(4)
где
-
подынтегральная функция;
-
подынтегральное выражение;
 -
произвольная постоянная.
-
произвольная постоянная.
Основные свойства неопределенного интеграла:
Постоянный множитель выносится за знак интеграла:
 .
.
Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций
 .
.
Для вычисления интегралов используют таблицу интегрирования элементарных функций
1.

2.

3.

4.

5.

6.

7.

8.

9.

10.
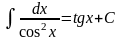
11.

12.

13.

14.

15.

16.

17.

18.

19.

Непосредственное интегрирование
1)
2)

3)

4)
5)

6)

7)

8)
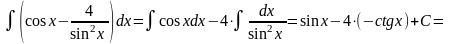

9)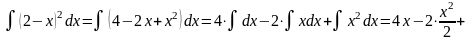

Интегрирование методом замены переменной (методом подстановки)
Найти неопределенные интегралы.






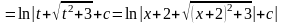

Интегрирование по частям в неопределенном интеграле
Формула интегрирования
по частям имеет вид:

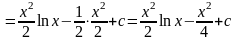










3.2 Определенный интеграл и его свойства. Формула Ньютона – Лейбница. Вычисление определенных интегралов
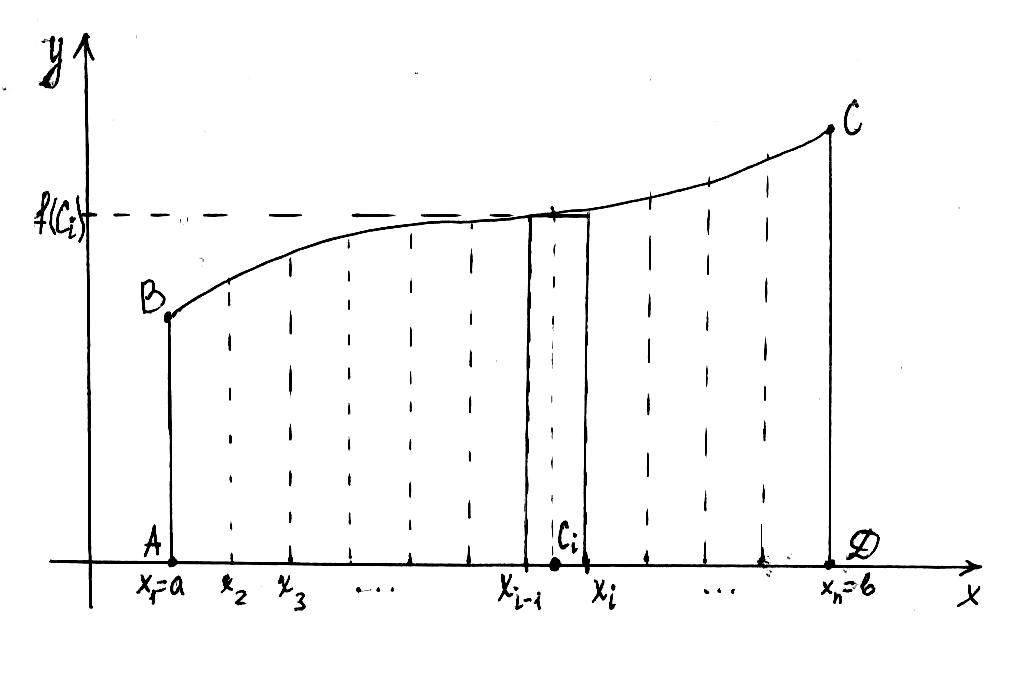
Рисунок 4 - Функция y=f(x), графиком которой является произвольная кривая
Рассмотрим функцию
y=f(x),
графиком которой является произвольная
кривая (рис.3 ). Она определена и непрерывна
на
 .
Разобьем
на n
одинаковых отрезков. Фигуру АВСД назовем
криволинейной трапецией. При указанном
построении трапеция разбилась на
несколько фигур, называемых также
криволинейными трапециями. Представим
их прямоугольниками: возьмем i-
отрезок, тогда длина данного прямоугольника
.
Разобьем
на n
одинаковых отрезков. Фигуру АВСД назовем
криволинейной трапецией. При указанном
построении трапеция разбилась на
несколько фигур, называемых также
криволинейными трапециями. Представим
их прямоугольниками: возьмем i-
отрезок, тогда длина данного прямоугольника
 .
Выберем произвольную точку
.
Выберем произвольную точку
 и вычислим значение функции
и вычислим значение функции
 - ширина прямоугольника. Для вычисления
площади прямоугольника нужно найти
произведение его длины на ширину:
- ширина прямоугольника. Для вычисления
площади прямоугольника нужно найти
произведение его длины на ширину:
 .
Тогда площадь все прямоугольников
криволинейной трапеции равна:
.
Тогда площадь все прямоугольников
криволинейной трапеции равна:

 - интегральная сумма.
- интегральная сумма.
Определение:
Если предел
 существует и не зависит от выбора точек
существует и не зависит от выбора точек
 ,
то функция f(x)
называется интегрируемой на
,
а такой предел называется определенным
интегралом от функции f(x)
на
и обозначается:
,
то функция f(x)
называется интегрируемой на
,
а такой предел называется определенным
интегралом от функции f(x)
на
и обозначается:
 - определенный
интеграл,
где a
и b
– нижний и верхний пределы интегрирования
соответственно.
- определенный
интеграл,
где a
и b
– нижний и верхний пределы интегрирования
соответственно.
Основные свойства определенного интеграла.
Интеграл не зависит от обозначения переменной:



Примеры:
1)

2)

3)
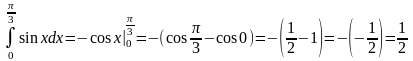
4)


5)
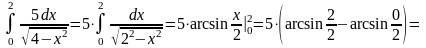

6)