Классификация простых категорических суждений по качеству и количеству

Поскольку каждое суждение одновременно имеет качественную и количественную характеристику, то будет целесообразным объединить два предыдущих разделения суждений по качеству и количеству В результате этого объединения получим такие че отиры типы простых суждений: загальностверджувальне А (SР) (от латинского - утверждать), частковостверджувальне И (SР), загальнозаперечне Е (SР) (от латинского слова - отрицать), частковозапе поперечной О (SР) Единичные по количеству суждения относят соответственно к загальностверджувальних или загальнозаперечних, поскольку в них речь идет не о части предметов данного класса, а об одном предмете, я кий составляет весь данный класс предметеів.

А (SР) - загальностверджувальне, есть общее по количеству и утвердительное по качеству, суждения Например, \"Любое преступление является уголовным поступком\" Его логическая формула: \"Все S есть Р\" кванторного слово \"все\" \"характеризует количество, а утвердительный логическая связка\" есть \"- качество суждениячна зв'язка "є" - якість судження.

I (SР) - частковостверджувальне, т.е. частичное по количеству и утвердительное по качеству суждения Например, \"Некоторые студенты являются отличниками учебы\" Его логическая формула: \"Некоторые S есть Р\" На количество су удження указывает кванторного слово \"некоторые\", а на качество - утвердительная логическая связка \"естьтверджувальна логічна зв'язка "є".

Е (SР)-загальнозаперечне, есть общее по количеству и отрицательное по качеству суждения Например, \"Ни один студент не является профессором\" Его логическая формула: \"Ни одно S не есть Р\" Количество суждение выражается к кванторного слова \"ни\", а качество - отрицательной логической связкой \"не являетсяперечною логічною зв'язкою "не є".

O (SР) - частковозаперечне, т.е. частичное по количеству и отрицательное по качеству суждения Например, \"Некоторые люди не являются студентами\" Его логическая формула: \"Некоторые S не есть Р\" На количество суждения указывает квант торне слово \"некоторые\", а на качество логическая связка \"не является на якість-логічна зв'язка "не є".

Логические формулы простого категорического суждения: \"Все S есть Р\", \"Некоторые S есть Р\", \"Ни одно S не есть Р\", \"Некоторые S не есть Р\" будем называть нормальными формами суждения

Для того, чтобы установить тип (А, Е, И, О) любого простого суждения необходимо:

1 Выяснить его смысл: утвердительное оно или отрицательное; что именно утверждается (отрицается), т.е. является S и Р суждения, о которой часть предметов 8 идет речь в суждении

2 Подать его в нормальной форме, S и Р при этом должны сохранять свои места согласно логического ударения первоначальной формы выражения Например, \"Бывают ошибки, похожие на истину\" 1) Интуит тивно ясно, что это суждение утвердительное; в нем S - \"недостатки\", а Р - \"истины\"; слово \"бывают\" указывает на то, что речь идет о части \"недостатков\" (S) Итак, 2) в нормальной и недостатки походят на истину \"(\" Некоторые S есть Р \") - это суждение I (SР) - частковостверджувальне Второй пример:\" не все одинаково пригодно для всех \"1) интуитивно ясно, что это суждение что-то отрицает,\" одинакового в пригодное \"- значит\" не пригодно \"или\" не пригоден \",\" не все \"- значит часть, то есть\" нечто \"(кстати, профессия, стиль жизни и т.п.); S -\" несколько \", а Р -\" форме оно будет таким \"Кое-что не пригоден для всех людей\" - это суждение O (SР) - частковозаперечн"придатне для всіх людей". Отже, 2) в нормальній формі воно буде таким "Дещо не є придатним для всіх людей" - це судження O(SР) - частковозаперечне.

8 Распределенность терминов в категорических суждениях

Срок (S, Р) считается распределенным, если его объем полностью включается или исключается из объема другого термина Распределенный термин обозначается - S, Р

Срок (S, Р) считается нераспределенной, если его объем частично включается или исключается из объема другого термина Нераспределенная термин обозначается - S-, Р-

зависимости от четырех типов простых категорических суждений существуют такие случаи распределенности терминов

Суждение А (SP)

Его формула: \"Все S есть Р\" Существует два случая распределенности S и Р

1-й случай Например, \"Все студенты-филологи являются студентами\" Отношения между 8 (студенты-филологи) и Р (студенты) представим в виде кругов Эйлера:

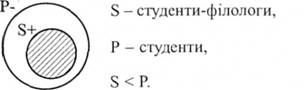
Поскольку \"все студенты - филологи\" включаются в объем предиката, то S будет распределенным В суждении логическое ударение стоит на S, то есть по объему \"студентов\" (Р) исключается та часть объема, которая относится к S Р-, таким образом, будет нераспределеннойм, буде нерозподіленим.

2-й случай Например, \"Все квадраты - прямоугольные ромбы\"

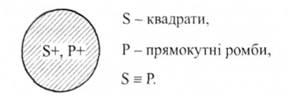
Это выделяя суждения, значит в нем объемы 8 и Р полностью совпадают или включают друг друга, тогда и Б, и Р будут распределенными

Суждение I (SР)

Его формула \"Некоторые S есть Р\" Существует два наиболее распространенных случая распределенности S и Р

1-й случай Например, \"Некоторые студенты являются отличниками учебы\"

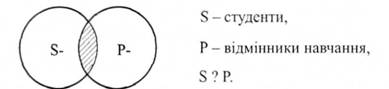
Отношение между объемами S и Р является неопределенным Поскольку S и Р частично включают объемы друг друга, то и S, и Р будут нераспределенными 2-й случай Например, \"Некоторые юристы являются адвокатами\"

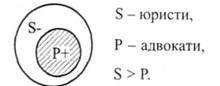
Поскольку все адвокаты (Р) включаются в объем S, то Р - будет распределенным Логическое ударение суждения стоит на Р, т.е. по объему юристов (S), исключается та часть объема, которая относится к Р, тогда и Б будет нераспределеннойм.

Суждение Е (SP)

Его формула \"Ни одно S не есть Р\" Здесь возможен только один случай распределенности S и Р Например, \"Ни кошка не является собакой\"

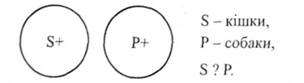
Поскольку и S, и Р полностью исключаются из объемов друг друга, то оба они будут распределены

Суждение O (SР)

Его формула \"Некоторые 8 не есть Р\" Здесь наиболее распространены два случая распределенности терминов

1-й случай Например, \"Некоторые юристы не являются адвокатами\"

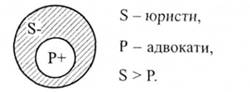
Поскольку речь идет о \"некоторых юристов\", то есть о части S, то субъект будет нераспределенной Предикат же полностью включается в объем субъекта, следовательно он будет распределенным

2-й случай Например, \"Некоторые студенты не являются отличниками учебы\"

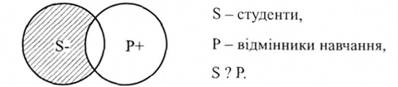
Поскольку S (студенты) частично (некоторые S) включается в объем Р (только частью студентов отличников), то S будет нераспределенной Р - отличники учебы - берется в полном объеме (полностью выключает ться по объему S).

Итак, S всегда распределен в общих суждениях и нераспределенная в частных; Р всегда распределен в отрицательных суждениях, а в утвердительных он будет распределенным при условии, что Р S

Для того, чтобы определить распределенность терминов в данном суждении необходимо:

1 Привести его к нормальной форме

2 Сформулировать обратное суждение, то есть поставить Р на первое место, а S на второе

3 Исходя из выявленного соотношения объемов S и Р, изобразить его кругами Эйлера

4 Проставить распределенность терминов Например, \"Электрон имеет отрицательный заряд\"

1 Нормальный форма: \"Все электроны являются отрицательно заряженными частицами\" - А (S Р)

2 Но А (S Р) имеет два случая соотношение объемов S и Р (S Р, S = Р) при одной и той же логической формуле: \"Все S есть Р\" В первом случае (S Р), обратное - \"Все Р есть S\" В нашем случае правильным обратным суждением будет: \"Все отрицательно заряженные частицы являются электронами\" Итакативно заряджені частки є електронами". Отже:

Утверждение о том, что \"Некоторые отрицательно заряженные частицы являются электронами\" было бы неверным, потому что кроме электрона таких частиц не существует