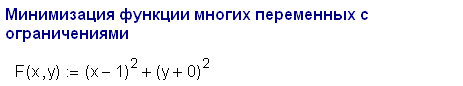2.2 Методы оптимизации

Математический аппарат автоматизированного проектирования связан с решением задач оптимизации. В оптимальном проектировании определяются элементы системы, или параметры, описывающие эти элементы. Эти элементы (или их параметры) фиксированы и поддерживаются в течение времени жизни изделия. Подобная ситуация часто именуется управлением с разомкнутой цепью.

Реальная конструкция это объект, на который наложены ограничения.

Применение ЭВМ при автоматизированном проектировании позволяет перейти от выработки более или менее хороших решений к выработке наилучших – оптимальных решений. Процесс выработки таких решений называется оптимизацией.

Зачастую при проектировании не гарантировано существование номинального проекта, удовлетворяющего заданным ограничениям, и еще меньше – существование оптимального проекта. Если даже оптимальный проект существует, то численные методы его построения зачастую оказываются довольно чувствительны к начальным значениям, и для сходимости итераций требуется искусство вычислителя.

Классическая постановка задачи оптимизации формулируется так. В некотором пространстве S тем или иным способом выделяется некоторое допустимое множество M точек этого пространства, называемое допустимым множеством. Далее фиксируется некоторая вещественная функция f(x), заданная во всех точках x допустимого множества. Она называется целевой функцией. Задача оптимизации состоит в том, чтобы найти точку x₀ в множестве М, для которой функция f(x) принимает максимальное (минимальное) значение. Т. е. для всех .

В такой постановке задача оптимизации может не иметь решения или может оказаться, что экстремум достигается во множестве точек.

В практических оптимизационных задачах приходится иметь дело с двумя основными видами постановок задачи:

1) Задача оптимизации функций. Задача ставится в обычном (евклидовом) пространстве конечной размерности. Точками x допустимого множества будет вещественные числа, а целевой функцией будет обычная вещественная функция от вещественных аргументов.

2) Задача оптимизации функционалов или вариационная задача. В качестве допустимого множества выступает множество M функций вещественных переменных y(x₁, …, x_m), а целевая функция есть функционал F, сопоставляющий каждой функции некоторое вещественное число F(y).

Постановка любой задачи оптимизации начинается с определения набора независимых переменных и обычно включает условия, которые характеризуют их приемлемые значения. Эти условия называют ограничениями задачи. Еще одной обязательной компонентой описания является скалярная мера «качества», именуемая целевой функцией и зависящая каким-то образом от переменных. Решение оптимизационной задачи – это приемлемый набор значений переменных, которому отвечает оптимальное значение целевой функции. Под оптимальностью обычно понимают максимальность или минимальность; например, речь может идти о максимизации прибыли или минимизации массы.

К задачам на поиск оптимума сводятся многие из математических проблем системного анализа, техники. В частности, они возникают при построении математических моделей. Когда для изучения какого-нибудь сложного явления конструируется математическая модель, к оптимизации прибегают для того, чтобы определить такую структуру и такие параметры последней, которые обеспечивали бы наилучшее согласование с реальностью. Другой традиционной областью применения оптимизации являются процедуры принятия решений, так как большинство из них нацелено именно на то, чтобы сделать «оптимальный» выбор. Помимо оптимизационных задач, представляющих самостоятельный интерес, на практике часто возникают задачи, которые «встроены» в некоторые вычислительные процессы, где они играют хотя и существенную, но все же вспомогательную роль. Это настолько типичная ситуация, что при описании процесса в целом далеко не всегда указывают на наличие подобных задач. К примеру, сказав, что процесс предполагает определение точки, в которой какая-то функция достигает своего критического значения, могут и не добавить, что эта точка будет найдена решением оптимизационной задачи.

Лучшие из современных программ поиска экстремума весьма сложны и действуют далеко неочевидным образом. Даже специалистам в области численных методов порой трудно определится с выбором подходящего для данной задачи метода. Поэтому используют классификацию методов по некоторым формальным признакам, позволяющих оценить эффективность метода в зависимости от характеристики задачи, а в случае неудачного решения наметить пути изменения стратегии решения.

Чаще всего используются универсальные методы, дающие приемлемые результаты по точности и экономичности. Но это относится к случаям, когда задача решается что называется «в лоб». Любые отклонения от накатанных путей требуют обычно более тонкого анализа задачи и подбора соответствующего метода.

Для решения разных классов задач оптимизации используют разные алгоритмы решения. Это является обычно соизмерением выгод от эксплуатации выделяемых свойств и затрат на разработку соответствующего математического обеспечения.

Наиболее очевидные различия между задачами связаны с математическими характеристиками их функций. Например, в одном случае целевая функция будет гладкой, а в другом – разрывной; иногда функции задачи просты и свойства их понятны, а иногда явные выражения для функций отсутствуют, и расчет их значений требует решения каких-то достаточно сложных подзадач.

Еще один показатель, который может существенно различаться для разных задач и всегда учитывается при выборе алгоритмов – это доступность производных. В одних задачах аналитические значения первых и вторых производных целевой функции вычисляются легко, а в других вычислению поддаются точные значения лишь самой функции. Когда говорят о доступности производных, то имеют в виду не только возможность построения процедуры расчета их точных значений, но и приемлемую трудоемкость этой процедуры. Последнее означает, что затраты на расчет производных сопоставляются с прочими затратами на реализацию поиска решения задачи.

Наконец, выбор алгоритма может определяться природой задачи и нуждами исследования, в рамках которого она возникла. Эти «внешние» факторы часто диктуют условия, никоим образом не вытекающие из математической постановки задачи. Например, по какой-то причине может оказаться необходимым, чтобы некоторые ограничения были соблюдены с большой точностью на всех итерациях. Суть задачи помимо прочего определяет и точность, с которой ее надо решить. Если, к примеру, результаты решения используются как второстепенные данные для некой внешней итерации, то тратить усилия на достижение максимальной точности бессмысленно. Немаловажно определить какая точность нас интересует: точность нахождения аргумента или близость значений функции к экстремуму.

Приведем примеры алгоритмов поиска оптимального решения.

Алгоритм наискорейшего спуска реализует итерационную процедуру движения к минимуму из произвольно выбранной точки начального приближения в направлении наиболее сильного уменьшения функции, определенном в окрестности текущего значения аргумента минимизируемой функции. Такое направление противоположно направлению, задаваемому вектором градиента минимизируемой функции

. (1)

Общая формула для нахождения значения аргумента X^(k+1) по значению X^(k), найденному на k-м шаге работы алгоритма наискорейшего спуска

, (2)

где – шаг градиентной процедуры – определяет число векторов единичной длины (если >0 – целое) или долей длины вектора (если  дробное), которое укладывается в направлении, противоположном градиенту при совершении (k+1)-го шага;

S^(k) – вектор единичной длины в направлении, противоположном направлению градиента f(X), определенном в точке X^(k) (далее будет использоваться обозначение )

. (3)

Норма вектора градиента равна:

. (4)

Геометрическая интерпретация алгоритма наискорейшего спуска: траектория X^(k) ортогональна линиям равного уровня минимизируемой функции. Последовательность сходится к точке X^*, в которой градиент g(X^*)=0. Важным для обеспечения сходимости метода имеет выбор шага на каждой итерации.

Чаще используются так называемые модифицированные методы Ньютона, различающиеся способами выбора шага, масштабированием, стратегией выбора направления и другими дополнительными свойствами, обеспечивающих устойчивость решения для определенного вида функций.

На базе классического метода Ньютона второго порядка строятся алгоритмы безусловной минимизации первого порядка, в которых не используются точные значения вторых производных. Когда вычисление аналитических значений вторых производных невозможно используются конечно-разностные приближения.

В отличие от упомянутых выше методов, в которых сведения о свойствах функции всегда относятся к одной точке, разработаны квазиньютоновские методы, в которых данные о кривизне функции накапливаются на основе ряда вычислений во время итераций. Далее используют формулы пересчета и условия применения поправок.

Для минимизации гладких функций используются модификации методов без аналитического вычисления производных. Выбор способа конечно-разностной аппроксимации производных зависит во многом от гладкости функции. Всегда одно упрощение влечет за собой дополнительные вычислительные затраты. К тому же вопрос об ошибках приближения производных остается открытым.

Среди задач поиска безусловного минимума особое место занимают задачи минимизации функции вида

. (7)

Задачи рассматриваемого типа возникают, например, при настройке математических моделей на реальные данные.

Для согласования модели с реальностью необходимо подобрать параметр X, при котором разности близки к нулю.

Одним из способов формализации данной задачи – рассмотрение ее как задачи поиска минимума суммы квадратов от f_i(X). Для решение используют методы, разработанные специально для задач о наименьших квадратов и обладающие особенностями по сравнению с общими методами минимизации. Например, методы Гаусса-Ньютона, Левенберга-Марквардта.

Решение задачи оптимизации в пакете Mathcad

Простейшими задачами оптимизации являются задачи на поиск экстремумов (минимумов и максимумов) функции одной переменной F(x). Если непрерывная функция F(x) имеет всего один экстремум, то задача его поиска оказывается достаточно простой – поскольку в точке экстремума производная F'(x)=0, то поиск экстремума сводится к решению указанного уравнения.

Однако если экстремумов несколько, то решение задачи резко усложняется. Самый высокий пик функции в этом случае именуют глобальным максимумом, а самый глубокий минимум – глобальным минимумом. Другие экстремумы называют локальными. Поиск глобальных экстремумов встречается только в высококлассных и сложных системах компьютерной математики (СКМ), тогда как поиск локальных экстремумов вблизи заданной точки или в заданной окрестности изменения аргумента F(x), есть практически во всех системах. В серьезных СКМ возможен ввод ограничивающих условий и при решении задач оптимизации нелинейных целевых функций. Более того, их встроенные или библиотечные функции оптимизации, как правило, решают как задачи оптимизации нелинейных функций, так и задачи линейного программирования.

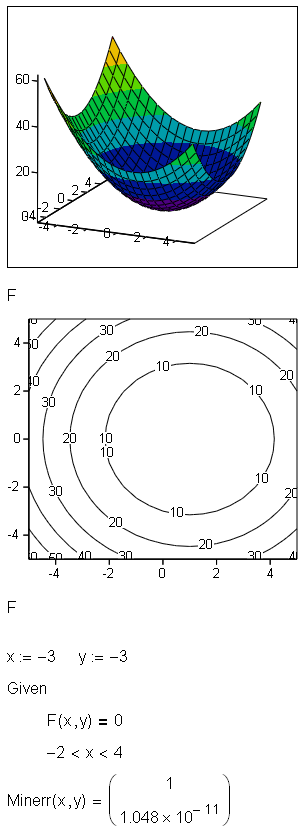
В практике расчетов основной интерес представляет оптимизация функций многих (N) переменных F(x₁, x₂,... , x_N). Такая функция представляет собой (N+1)-мерную поверхность. Большое число задач в науке и в технике сводится к решению задачи на поиск максимума или минимума функции многих переменных – проектных параметров, обычно называемой целевой функцией.

Обычно в СКМ реализуются несколько методов поиска экстремумов, и они применяются в зависимости от особенностей анализируемой функции и успеха применения некоторых начальных методов.

Ниже приведен пример решения задачи в пакете Mathcad.