2 Решение задач математического моделирования
2.1 Аппроксимация данных методом наименьших квадратов
Детерминированная функциональная зависимость Y=fun(X) встречается на практике редко, так как при измерениях величин Х и Y всегда имеются ошибки и влияние случайных, не учитываемых факторов. Причем каждая из величин Х и Y может зависеть как от одних и тех же, так и от различных случайных факторов.
В общем случае можно считать, что Y зависит от Х случайным образом и эту зависимость можно определить с помощью известных из теории вероятности характеристик многих случайных величин, таких как совместное распределение вероятности, условная плотность распределения, коэффициенты корреляции, моменты и пр.
На практике встречается много частных постановок задач установления статистической связи. Так, часто встречается вид функциональной связи (линейная, квадратичная и пр.), и требуется определить только числовые значения параметров этой зависимости по полученным в результате эксперимента значениям Х и Y. Иногда при этом путем последовательных проб подбирается и наилучший вид детерминированной функциональной зависимости (линейная или квадратичная) – это задача аппроксимации расчетной неизвестной нелинейной функции аналитическим выражением.
Наиболее распространенным и эффективным способом решения этой задачи является метод наименьших квадратов.
Допустим, что имеется совокупность двух случайных величин Х и Y и известен вид функциональной зависимости между ними F(x). Требуется провести через эти точки кривую наилучшим образом. Понятие «лучшее» математически может быть выражено различным способом. Проводить непосредственно через точки неправильно, так как очевидно, что разброс вызван ошибками измерений. Например, можно потребовать, чтобы сумма абсолютных значений расстояний точек от кривой была минимальна или максимальное отклонение было минимальным и пр. Но наиболее распространенным критерием оптимальности является минимум суммы квадратов отклонений
![]() .
.
Критерий минимума суммы квадратов часто применяется по трем соображениям. Во-первых, при этом большое количество задач оказывается возможным решить аналитически. Во-вторых, при квадратичной зависимости получается, что ущерб (сожаление) при малых значениях ошибок мал, а с их увеличением резко возрастает. Это обстоятельство правильно отражает практическую ситуацию, так как малые ошибки менее опасны, чем большие. И, наконец, при этом критерии удовлетворяется критерий максимума правдоподобия для случая, когда отклонения подчиняются нормальному закону распределения.
При полиномиальной регрессии степень аппроксимирующего полинома должна быть меньше количества исходных точек. Не рекомендуется делать степень выше 4 – 6, поскольку погрешности реализации регрессии сильно возрастают.
Выбор вида аппроксимирующей функции и метода решения зависит от физической сущности задачи, особенностей искомой функции, программного обеспечения и самого исследователя.
Для поиска минимума средних квадратических отклонений и определения коэффициентов аппроксимирующей функции используются методы минимизации.
Справочный материал
В пакете Mathcad имеются следующие встроенные функции:
regress(X, Y, k) – вычисление вектора коэффициентов для полиномиальной регрессии;
interp(S, X, Y, t) – вычисление интерполяции;
linfit (X, Y, F) – вычисление вектора коэффициентов регрессии в виде линейной комбинации функций;
где X, Y – векторы исходных данных;
t – аргумент аппроксимирующей функции;
S – вектор коэффициентов полинома;
F(t) – пользовательская функция.
Порядок выполнения работы
Получить свои варианты заданий.
Провести в системе MATHCAD расчет для различных аппроксимирующих функций.
Построить график полученной функции и исходных точек.
Оценить степень приближения.
Сделать выводы о характере и причинах расхождения графических зависимостей.
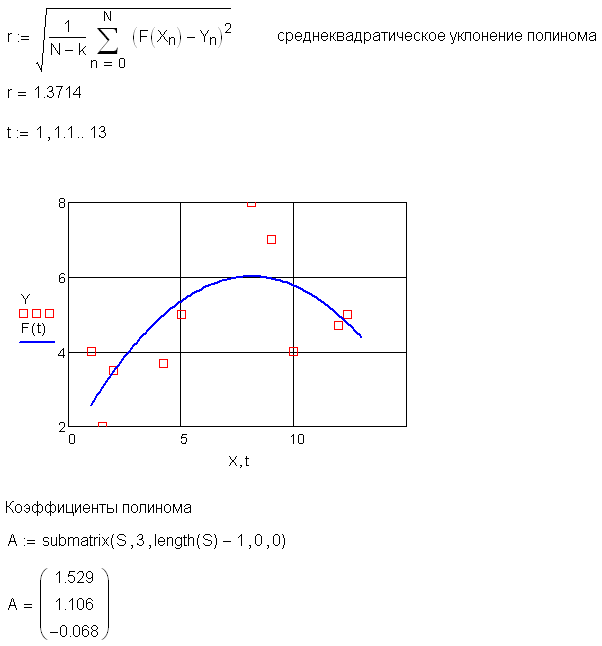
Ниже приведен пример решения задачи в пакете Mathcad.