2) Тригонометрические фу́нкции — математические функции от угла. Они безусловно важны при изучении геометрии, а также при исследованиипериодических процессов. Обычно тригонометрические функции определяют как отношения сторон прямоугольного треугольника или длиныопределённых отрезков в единичной окружности. Более современные определения выражают тригонометрические функции через суммы рядовили как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на произвольныевещественные числа и даже на комплексные числа.

В настоящее время выделяют шесть основных тригонометрических функций, указанных ниже вместе с уравнениями, связывающими их друг с другом. Для последних четырёх функций, эти соотношения часто называютопределениями этих функций, однако можно определять эти функции геометрически или как-нибудь по-другому. Кроме того, существуют другие функции, такие как   и  , но они в настоящее время редко используются (см. Редко используемые тригонометрические функции). С тригонометрическими функциями тесно связаны обратные им функции (см. Обратные тригонометрические функции)

Функция	Обозначение	Соотношение
Си́нус
Ко́синус
Та́нгенс	или
Кота́нгенс	или
Се́канс
Косе́канс	или
Основные тригонометрические функции

3)

Формула	Допустимые значения аргумента	Номер
		(1)
		(2)
		(3)
		(4)

4) Формулы сложения аргументов

sin(α + β) = sinα cosβ + cosα sinβ cos(α + β) = cosα cosβ - sinα sinβ

tg(α + β)	=	tgα + tgβ
		1 - tgα tgβ

ctg(α + β)	=	ctgα ctgβ - 1
		ctgα + ctgβ

sin(α - β) = sinα cosβ - cosα sinβ cos(α - β) = cosα cosβ + sinα sinβ

tg(α - β)	=	tgα - tgβ
		1 + tgα tgβ

ctg(α - β)	=	ctgα ctgβ + 1
		ctgα - ctgβ

5)

Формулы для двойных углов

Для любого угла α справедливы равенства:

sin 2α = 2sinα cosα

cos 2α = cos2α – sin2α = 2 cos2α – 1 = 1 – 2sin2α

Для любого угла α такого, что α ≠ π/2 + πk, α ≠ π/4 + πn/2 (k, n принадлежат множеству Z), справедливо:

tg 2α = 2 tgα/(1 – tg2α)

Для любого угла α такого, что α ≠ πk/2 (k принадлежит множеству Z), справедливо:

сtg 2α = (ctg2α – 1)/(2ctgα)

Формулы для половиннных углов

Для любого угла α справедливы равенства:

cos2α/2 = (1 + cos α)/2

sin2α/2 = (1 – cos α)/2

Для любого угла α такого, что α ≠ π + 2πk (k принадлежит множеству Z), справедливо:

tg2α/2 = (1 – cosα)/(1 + cosα)

ctg2α/2 = (1 + cosα)/(1 – cosα)

tgα/2 = sin α/(1 + cosα)

cos α = (1 – tg2α/2)/(1 + tg2α/2)

sin α = (2 tgα/2)/(1 + tg2α/2)

Для любого угла α такого, что α ≠ πk (k принадлежит множеству Z), справедливо:

tgα/2 = (1 – cosα)/(sin α)

ctgα = (1 – tg2α/2)/(2 tgα/2)

Для любого угла α такого, что α ≠ π + 2πk и α ≠ π/2 + πn (k, n принадлежат множеству Z), справедливо:

tg α = (2 tg α/2)/(1 – tg2α/2)

6)Формулы приведения

В таблице даны формулы приведения для тригонометрических функций.

Функция (угол в º)	90º - α	90º + α	180º - α	180º + α	270º - α	270º + α	360º - α	360º + α
sin	cos α	cos α	sin α	-sin α	-cos α	-cos α	-sin α	sin α
cos	sin α	-sin α	-cos α	-cos α	-sin α	sin α	cos α	cos α
tg	ctg α	-ctg α	-tg α	tg α	ctg α	-ctg α	-tg α	tg α
ctg	tg α	-tg α	-ctg α	ctg α	tg α	-tg α	-ctg α	ctg α
Функция (угол в рад.)	π/2 – α	π/2 + α	π – α	π + α	3π/2 – α	3π/2 + α	2π – α	2π + α

7)

Четность тригонометрических функций. Углы φ и —φ образуются при повороте луча в двух взаимно противоположных   направлениях   (по  часовой  стрелке и  против часовой стрелки).
Поэтому конечные стороны OA1 и ОА2 этих углов симметричны относительно оси абсцисс. Координаты векторов единичной длины OA1 = (х1 , у1) и ОА2 = (х2, y2) удовлетворяют соотношениям:                 х2 = х1    y2 = —у1               Поэтому cos(—φ) = cosφ, sin (— φ) = —sin φ, Следовательно, синус является нечетной, а косинус — четной функцией угла.
Далее имеем:
Поэтому   тангенс   и  котангенс   являются   нечетными функциями угла.

8)Обра́тныетригонометри́ческиефу́нкции — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

• аркси́нус (обозначение: arcsin)

• аркко́синус (обозначение: arccos)

• аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)

• арккота́нгенс (обозначение: arcctg; в иностранной литературе arccotan)

• арксе́канс (обозначение: arcsec)

• арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin⁻¹ для арксинуса и т.п.; это считается неоправданным, так как возможна путаница с возведением функции в степень −1.

9)Свойства функции arcsin

 (функция является нечётной).  при  .

 при 

 при 

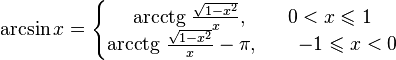
Свойства функции arccos[

•  (функция центрально-симметрична относительно точки  ), является индифферентной.

•  при 

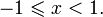
•  при 

• 

• 

• 

• 

• 

Свойства функции arctg

• 

• , при x > 0.

Свойства функции arcctg

•  (график функции центрально-симметричен относительно точки 

•  при любых 

• 

11)

12)Степенью  числа a > 0 с рациональным показателем является степень, показатель которой представим в виде  обыкновенной несократимой дроби x = m/n, где m целое, а n натуральное число, причём n > 1 (x - показатель степени).

13) Степень с действительным показателем

Пусть дано положительное число   и произвольное действительное число  . Число  называется степенью, число   — основанием степени, число   — показателем степени.

По определению полагают:

• .

• .

• ,  .

Если   и   — положительные числа,   и   — любые действительные числа, то справедливы следующие свойства:

• .

• .

• .

• .

• .

• .

14)Логари́фм числа   по основанию   (от греч. λόγος — «слово», «отношение» и ἀριθμός — «число»^[1]) определяется^[2] какпоказатель степени, в которую надо возвести основание  , чтобы получить число  . Обозначение:  , произносится: "логарифм   по основанию  ".