23 Дисперсия альтернативного признака.

Дисперсия имеет большое значение в экономическом анализе. В математической статистике важную роль для характеристики качества статистических оценок играет их дисперсия. разложение дисперсии на соответствующие элементы, позволяет оценить влияние различных факторов, обуславливающих вариацию признака; использование дисперсии для построения показателей тесноты корреляционной связи при оценке результатов выборочных наблюдений. Альтернативными называются 2 взаимоисключающих друг друга признака. То признаки, которыми каждая отдельная единица совокупности либо обладает, либо не обладает. Наличие альтернативного признака принято обозначать через единицу, а отсутствие через 0. Долю единиц обладающих данным признаком обозначают через p (п), а долю единиц на обладающих данным признаком обозначают через q. При этом p+q=1.

Дисперсия альтернативного признака определяется по формуле:

Альтернат.признак-приним.одно из2-х взаимоисключ.друг друга значений. σ² = p*q,где p+q=1 q=1-p ,следовательно

σ² =p*(1-p) . p-доля ед-ц, облад-х интересующим нас св-вом кач-ва.. q-доля ед-ц не облад.этими св-ми кач-ва. Мах.неоднородность совок. альтер.-вальирующему признаку будет в том случае, если доля облад-х интерс.-х признаков, и доля необлад.им будут равны.

24 Виды дисперсии и правило их сложения.

. Вар-ция, обусл. влиянием ф-ра, положен. в осн. группировки - межгруп. вар-цией и х-зуется межгруп. дисп. (d²).

Межгруп. дисп. явл. мерой колеблемости частных средних 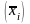около общей средней :

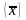, где f – кол-во ед-ц сов-ти в каждой i-й группе.

Вар-цию, обусл. влиянием прочих ф-ров, х-зует в каждой группе внутригруп. дисп. :

.

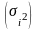Ср. из внутригруп., или частных дисп-й опред. по ф-ле ср. арифм. взв. дисп-й групп:

.

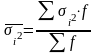Общая дисп. призн. = сумме межгруп. и ср. арифм. внутригруп. дисп-й:

.

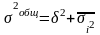Отнош. межгруп. дисп. к общей дает коэф. детермин. (h²). Данный коэф. х-ет, какая доля всей в-ции призн. обусл. признаком, положен. в осн. группировки:

.

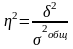Корень квадратный из коэф. детерминации дает эмпирич. корреляционное отнош, кот. хар-ет тесноту связи между группировочным и результативным признаками:

.

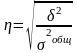Этот показатель изменяется от 0 до 1

24.Виды дисперсии и правило их сложения.

Дисперсия: σ² = (x-x)²/n - для не сгруппир. данных; σ² = (x-x)²f/f - для сгруппир. данных. Сущ. правило: σ²_об = ² + σ²_i;² – межгрупп. дисп. (х-ет вар-ю пр-нака сов-ти под влиянием фактора, полож. в основание группировки);σ²_i– ср-яя из групповых дисп-я (показ. вар-ю пр-наков сов-ти под влиянием всех прочих ф-ров, кроме ф-ра, положенного в основание группировки); σ²_об – общая дисп., показ. вар-ю пр-нака в сов-ти под влиянием всех возможных ф-ров. ² = ²/σ²_об; ² – коэфф. детерминации, показ. долю вар-ии пр-наков в сов-ти, сформир-ся под влиянием ф-ра полож. в основание группир.. ² =  - это эмпирическое корреляционное отношение, кот. х-ет (измеряет) тесноту связи между ф-рами Х и результативными пр-наками. Если эмпир. корел. отнош. находится: 0,1 – 0,3 - связь слабая; 0,3 – 0,5 – умер.; 0,5 – 0,7 – заметная; 0,7 – 0,9 – тесная; 0,9 – 0,99 - очень тесная или близкая к функциональной.