Пример 1

Лестница длиной L приставлена под углом к гладкой вертикальной стене, на верхнем конце имеются ролики. Лестница весит P. На расстоянии l от ее верхнего конца подвешен груз W. Найдите:

1. силу давления роликов на стену

2. горизонтальную и вертикальную составляющие силы, с которой лестница давит на землю.

19

Работой A, совершаемой постоянной силой   называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус углаα между векторами силы   и перемещения   (рис. 1.18.1): 

A = Fs cos α.

Работа является скалярной величиной. Она может быть как положительной (0° ≤ α < 90°), так и отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж).

Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.

Рисунок 1.18.1. Работа силы  :

Если проекция   силы   на направление перемещения   не остается постоянной, работу следует вычислять для малых перемещений Δs_i и суммировать результаты: 

21 Общее уравнение динамики   – при движении системы с идеальными связями в каждый данный момент времен сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю. Уравнение использует принцип возможных перемещений и принцип Даламбера и позволяет составить дифференциальные уравнения движения любой механической системы. Дает общий метод решения задач динамики. Последовательность составления: а) к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силы и моменты пар сил инерции; б) сообщают системе возможные перемещения; в) составляют уравнения принципа возможных перемещений, считая систему находящейся в равновесии.

22

23Возможные (виртуальные) перемещения системы (ds, dj) – любая совокупность бесконечно малых перемещений точек системы, допускаемых в данный момент наложенными на систему связями. Возможные перемещения рассматривают как величины первого порядка малости, пренебрегая при этом величинами высших порядков малости. Т.е. криволинейные перемещения точек заменяют прямолинейными отрезками, отложенными по касательным к их траекториям.

25В аналитической механике наряду с понятием о силе как векторной величине, характеризующей воздействие на данное тело со стороны других материальных тел, используют понятие об обобщенной силе. Для определения обобщенной силы рассмотрим возможную работу сил, приложенных к точкам системы,

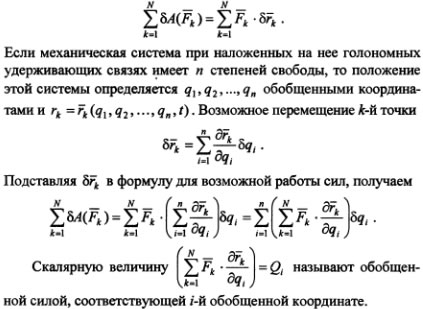
Таким образом, обобщенной силой, соответствующей i-й обобщенной координате, называется величина, равная коэффициенту при вариации данной обобщенной координаты в выражении возможной работы сил, действующих на механическую систему.

В общем случае обобщенная сила является функцией обобщенных координат, скоростей точек системы и времени. Из определения следует, что обобщенная сила — скалярная величина, которая зависит от выбранных для данной механической системы обобщенных координат. Это значит, что при изменении набора обобщенных координат, определяющих положение данной системы, изменятся и обобщенные силы. Так, для диска радиусом r и массой m, который катится без скольжения по наклонной плоскости (рис. 18.8), за обобщенные координаты можно принять либо s — координата центра масс диска, либо "фи" — угол поворота диска. Если пренебречь сопротивлением качению, то в пер-

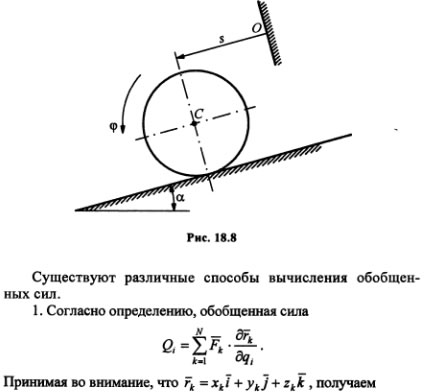
2. Обобщенные силы для механических систем с n > 1 целесообразно вычислять последовательно, учитывая, что обобщенные координаты, а значит, и их вариации независимы между собой. Системе всегда можно сообщить такое возможное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не варьируются. В этом случае:

27

Уравнения Лагранжа второго рода – это дифференциальные уравнения движения механической системы в обобщенных координатах. Как и раньше, считаем, что связи, наложенные на систему, − голономные, стационарные и идеальные. Для получения уравнений движения воспользуемся общим уравнением динамики:   .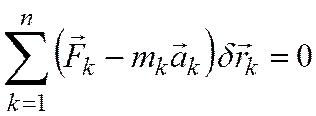

Для системы со стационарными связями виртуальное перемещение  -й точки  выражается, как было показано раньше, через обобщенные координаты соотношением   . 

Подстановка его в общее уравнение динамики дает:

.

 

Перегруппируем слагаемые, меняя порядок суммирования,

 

.

 

Так как связи голономные, то вариации обобщенных координат   независимы. Следовательно, коэффициенты при вариациях обобщенных координат равны нулю.

То есть 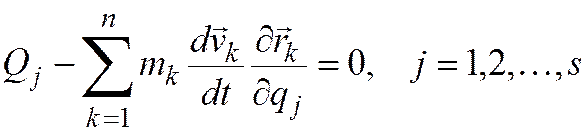 .  (21.1)  Так как    ,  то с учетом тождеств  Лагранжа имеем:   . (21.2)

 

 

Подставляя  соотношение (21.2) в равенство (21.1), внося   под знаки производных и меняя порядок суммирования и дифференцирования, получаем 

    или  

.

 

Полученная система дифференциальных уравнений называется уравнениями движения механической системы в обобщенных координатах  (уравнения Лагранжа второго рода).  Разность полной производной по времени от частной производной от кинетической энергии по обобщенной скорости и частной производной от кинетической энергии по обобщенной координате равна обобщенной силе.

Если связи, наложенные на систему, неидеальные, то при составлении уравнений движения следует реакции неидеальных связей отнести к активным силам. Уравнения Лагранжа имеют место и для нестационарных связей.

28

Для консервативной механической системы обобщенные силы определяются через потенциальную энергию системы соотношениями:  .

Тогда уравнения Лагранжа перепишутся в виде   .

 

Введем функцию Лагранжа   соотношением:  .  Учитывая, что потенциальная энергия есть функция только обобщенных координат   , имеем    .

 

Если в функцию Лагранжа не входят явно   обобщенных координат  , то возможно частичное интегрирование дифференциальных уравнений движения механической системы. Соответствующие обобщенные координаты называются циклическими. Для них   .

 

Тогда   откуда находим    общих интегралов системы дифференциальных уравнений движения механической системы   .