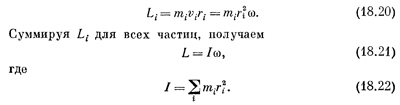1. Механическая система обладает определённым числом 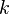  степеней свободы, а её состояние описывается с помощью обобщённых координат 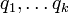  и соответствующих им обобщённых импульсов  . Задача механики состоит в изучении свойств механических систем, и, в частности, в выяснении их эволюции во времени.

Являясь одним из классов физических систем, механические системы по характеру взаимодействия с окружением разделяются на изолированные (замкнутые), закрытые и открытые, по принципу изменения свойств во времени — на статические и динамические.

Наиболее важными механическими системами являются:

• материальная точка

• неголономная система

• гармонический осциллятор

• математический маятник

• физический маятник

• крутильный маятник

• абсолютно твёрдое тело

• деформируемое тело

• абсолютно упругое тело

• сплошная среда

Рассмотрим пример интегрирования системы для простейшего случая, когда .

Пусть груз массой на пружине с жесткостью совершает колебания в вертикальном направлении под действием вынуждающей силы, проекция которой на ось :

Определить, при каких условиях эти колебания можно погасить за счет крепления к первому грузу второго с массой через пружину с жесткостью .

Учитываем силы, действующие на обе массы за счет удлинения пружин, отсчитываемого от положения статического равновесия каждого груза.

Тогда первый груз движется под действием силы упругости пружины с коэффициентом жесткости , пружины с коэффициентом жесткости , расположенной между телами, и вынуждающей силы. Дифференциальное уравнение движения первого груза в проекции на ось имеет вид:

Второй груз движется только под действием пружины с коэффициентом жесткости , и дифференциальное уравнение движения его будет иметь вид:

Решать эту систему уравнений нужно совместно. При этом нас интересует случай гашения колебаний первого груза, т. е. условия, когда . При выполнении этого условия уравнения движения принимают вид:

Из первого уравнения выражаем , дважды дифференцируем и подставляем во второе. После сокращения получим:

Это и есть условие гашения колебаний - его можно выполнить, подбирая либо массу, либо жесткость пружины, либо то и другое. При этом слишком малое значение массы (из требования минимума дополнительного веса) может привести к малому , а это даст очень большую амплитуду колебаний дополнительной массы.

Решение такого рода задач при количестве масс , как отмечено выше, возможно только в некоторых исключительных случаях. Поэтому далее рассматриваем движения системы как некоторого целого образования, так что определим закон движения центра масс системы.

Возьмем за основу систему уравнений (1) и почленно сложим ее левые и правые части - получим уравнение (2).

Формула радиуса-вектора центра масс имеет вид:

Беря вторую производную от обеих частей этого равенства, получим в уравнении (2):

Запишем теорему о движении центра масс системы:

Проектируя это уравнение на оси системы координат, получим:

2. Аксиомы динамики Законы динамики обобщают результаты многочисленных опы­тов и наблюдений. Законы динамики, которые принято рассматри­вать как аксиомы, были сформулированы Ньютоном, но первый и , четвертый законы были известны Галилею. Механику, основанную на этих законах, называют классической механикой. Первая аксиома (принцип инерции) Всякая изолированная материальная точка находится в стоянии покоя или равномерного и прямолинейного движения, приложенные силы не выведут ее изэтого состояния. Это состояние называют состоянием инерции. Вывести из этого состояния, т.е. сообщить ей некоторое ускорение, внешняя сила. Всякое тело (точка) обладает инертностью. Мерой инертности является масса тела. Массой называют количество вещества в объеме тела, в классической механике ее считают величиной постоянной. Единица измерения массы — килограмм (кг). Вторая аксиома (второй закон Ньютона — основной закон динамики) Зависимость между силой, действующей на материальную точку, и сообщаемым ею ускорением следующая: F = та, где т — масса точки, кг; а — ускорение точки, м/с². Ускорение, сообщенное материальной точке силой, nponoрционально величине силы и совпадает с направлением силы. Основной закон динамики в дифференциальной форме: На все тепа на Земле действует сила тяжести, она телу ускорение свободного падения, направленное к центру Земли: G = mg, где g = 9,81 м/с², ускорение свободного падения.  Третья аксиома (третий закон Ньютона) Силы взаимодействия двух тел равны по величине и направлены по одной прямой в разные стороны (рис. 13.1): При взаимодействии ускорения обратно пропорциональны мас­сам. Четвертая аксиома (закон независимости действия сип) Каждая сила системы сил действует так, как она действовала бы одна. Ускорение, сообщаемое точке системой сил, равно геометриче­ской сумме ускорений, сообщенных точке каждой силой в отдельно­сти.

В основе динамики лежат законы, установленные путем обобщения результатов целого ряда опытов и наблюдений над движением тел и проверенные обширной общественно-исторической практикой человечества. Систематически эти законы были впервые изложены И. Ньютоном.  

Первый закон (закон инерции), открытый Галилеем, гласит: изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямо­линейного движения до тех пор, пока приложенные силы не за­ставят ее изменить это состояние. Движение, совершаемое точ­кой при отсутствии сил, называется движением по инерции.

Закон инерции отражает одно из основных свойств материи - пребывать неизменно в движении и устанавливает для материальных тел эквивалентность состояний покоя и движения по инерции. Из него следует, что если F=0, то точка покоится или движется с постоян­ной по модулю и направлению скоростью  (   =const); ускорение точки при этом равно нулю:   = 0); если же движение точки не является равномерным и прямолинейным, то на точку действует сила.

Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной системой отсчета (иногда ее условно называют неподвижной). По данным опыта для нашей Сол­нечной системы инерциальной является система отсчета, начало кото­рой находится в центре Солнца, а оси направлены на так называемые неподвижные звезды. При решении большинства технических задач инерциальной, с достаточной для практики точностью, можно считать систему отсчета, жестко связанную с Землей.

Второй закон (основной закон динамики)  гласит: произведение массы точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы.

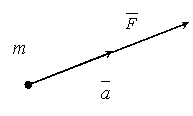
Математически этот закон выражается векторным равенством    .

При этом между модулями ускорения и силы имеет место зависимость   ma = F.       

Второй закон динамики, как и первый, имеет место только по отношению к инерциальной системе отсчета. Из этого закона непо­средственно видно, что мерой инертности материальной точки является ее масса, так как две разные точки при действии одной и той же силы получают одинаковые ускорения только тогда, когда будут равны их массы; если же массы будут разные, то точка, масса кото­рой больше (т. е. более инертная), получит меньшее ускорение, и наоборот.

Если на точку действует одновременно несколько сил, то они, как известно, будут эквивалентны одной силе, т.е. равнодействую­щей  , равной геометрической сумме этих сил. Уравнение, выражаю­щее основной закон динамики, принимает в этом случае вид

 или  .

Третий закон (закон равенства действия и противодействия) устанавливает характер механического взаимодействия между мате­риальными телами. Для двух материальных точек он гласит: две ма­териальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.         

 

Заметим, что силы взаимодействия между свободными материаль­ными точками (или телами), как приложенные к разным объектам, не образуют уравновешенной системы.

Проведём небольшой эксперимент. Попробуем перемещать тяжёлое тело по некоторой криволинейной траектории. Сразу обнаружим, что тело сопротивляется изменению направления движения, изменению скорости. Возникает сила со стороны тела, противодействующая силе  , той, которую мы прикладываем к нему.

Эту силу, с которой материальная точка сопротивляется изменению своего движения, будем называть силой инерции этой точки -  . По третьему закону она равна и противоположна действующей на точку силе  ,  . Но на основании второй аксиомы  . Поэтому  .

Итак, сила инерции материальной точки по величине равна произведению её массы на ускорение

.

И направлена эта сила инерции в сторону противоположную вектору ускорения.

Например, при движении точки по кривой линии ускорение  . Поэтому сила инерции

.

То есть её можно находить как сумму двух сил: нормальной силы инерции и касательной силы инерции.

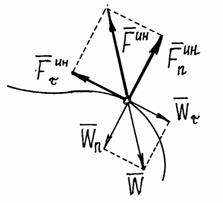
Рис.1

 

Причём

   

Необходимо заметить, что сила инерции материальной точки, как сила противодействия, приложена не к точке, а к тому телу, которое изменяет её движение. Это очень важно помнить.

Третий закон динамики, как устанавливающий характер взаимодей­ствия материальных частиц, играет большую роль в динамике системы.

Четвертый закон (закон независимого действия сил). При одновременном действии на материальную точку нескольких сил ускорение точки относительно инерционной системы отсчета от действия каждой отдельной силы не зависит от наличия  других, приложенных к точке, сил и полное ускорение равно векторной сумме ускорений от действия отдельных сил.

;      

Важную роль в развитии естествознания сыграл принцип относительности для механического движения, впервые установленный Г. Галилеем и окончательно сформулированный в механике И. Ньютоном. Для его понимания потребуется ввести понятие системы отсчета, или координат. Как известно, положение движущегося тела в каждый момент времени определяется по отношению к некоторому другому телу, которое называется системой отсчета и с которым может быть жестко связана система координат. Таким образом, механическое движение тогда относительно, и его описание зависит от того, по отношения к какой системе координат оно рассматривается. Среди систем отсчета особо выделяются инерциальные системы, которые находятся друг относительно друга либо в покое, либо равномерном и прямолинейном движении. Смысл принципа относительности Галилея заключается в том, что во всех инерциальных системах отсчета законы классической механики имеют одинаковую математическую форму записи. По существу, это означает, что из совокупности инерциальных систем невозможно выделить какую-либо одну преимущественную систему. Например, на судне, движущемся равномерно, тело, выпущенное из рук, падает вертикально вниз независимо от того, стоит судно или движется; вода, налитая в сосуд, на движущемся судне, как и в покое, имеет горизонтальную поверхность; на движущемся корабле при выстреле пуля летит столько же времени от носа к корме, сколько от корме к носу, и т.д. Для описания механических движений в разных инерциальных системах координат обычно пользуются так называемыми преобразованиями Галилея, которые выражают связь координат материальной точки в условно движущейся (х’, у’, z’) со скоростью V в момент времени t и условно неподвижной (x,y,z) системах координат Очевидно, что координаты точки А в движущейся системе (х’, у’, z’) связаны с координатами этой же точки в неподвижной системе (х,y,z) следующими соотношениями х’ = x-Vt; у’ = у, z’ = z. В классической механике, например, закон сложения скоростей выглядит следующим образом. Пусть материальная точка А движется в системе координат х’, у’, z’ со скоростью U, а сама система координат (х’, у’, z’) движется со скоростью V относительно системы координат (х, у, z). Тогда в системе координат (x,y,z) точка А будет двигаться со скорость W = U + V . Действительно, по определению скорость U = х = х ±Vt (преобразование Галилея). Из преобразований Галилея следует, что при переходе от одной инерциальной системы к другой такие величины, как координаты тела, скорость, импульс, кинетическая энергия, изменяются. А такие величины, как время, масса, ускорение, сила, и, следовательно, все законы Ньютона, при подобных преобразованиях остаются неизменными, т.е. инвариантными. Это и отражено в механическом: принципе относительности Галилея. 4 Из теоремы об изменении количества движения системы следует, что в отсутствие внешних сил (замкнутая система), а также при равенстве суммы всех внешних сил нулю выполняется   и  . Иначе говоря, справедливо соотношение

Таким образом, следует вывод:

Если сумма всех внешних сил, действующих на систему, равна нулю, то количество движения (импульс) системы есть величина постоянная.

Данное утверждение составляет содержание закона сохранения количества движения системы^[2][3].

Возможны случаи, когда сумма внешних сил нулю не равна, но равна нулю её проекция на какое-либо направление. Тогда равно нулю и изменение проекции количества движения системы на это направление, т. е., как говорят, сохраняется количество движения в этом направлении.

Количеством движения системы будем называть векторную величину  , равную геомет­рической сумме (главному вектору) количеств движения всех точек системы (рис.44):

Из чертежа видно, что независимо от величин скоростей точек системы (если только эти скорости не параллельны) вектор   может принимать любые значения и даже оказаться равным нулю, когда многоугольник, построенный из векторов  , замкнется. Следова­тельно, по величине   нель­зя полностью судить о ха­рактере движения системы.                                                                

Рис.44

 

Найдем формулу, с по­мощью которой значительно легче вычислять величину  , а также уяснить ее смысл.

Из равенства   следует, что 

Беря от обеих частей производную по времени, получим

 или   

Отсюда находим, что 

т.е. количество движения системы равно произведению массы всей системы на скорость ее центра масс. Этим результатом особенно удобно пользоваться при вычислении количеств движения твердых тел.

Из формулы видно, что если тело (или система) движется так, что центр масс остается неподвижным, то количество движения тела равно нулю. Например, количество движения тела, вращающегося вокруг неподвижной оси, проходящей через его центр масс, будет равно нулю.

Если же движение тела является сложным, то величина   не будет характеризовать вращательную часть движения вокруг центра масс. Например, для катящегося колеса   независимо от того, как вращается колесо вокруг его центра масс С.

Таким образом, количество движения характеризует только поступательное движение системы. При сложном же движении величина   характеризует только поступательную часть движения системы вместе с центром масс.

5. Из теоремы об изменении количества движения системы можно получить следую­щие важные следствия:

1) Пусть сумма всех внешних сил, действующих на систему, равна нулю:

Тогда из уравнения   следует, что при этом  . Таким образом, если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянен по модулю и направлению.

2) Пусть внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например Оx) равна нулю:

Тогда из уравнения   следует, что при этом  . Таким образом, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция количества движения системы на эту ось есть величина постоянная.

Эти результаты и выражают закон сохранения количества движения системы. Из них следует, что внутренние силы изменить суммарное количество движения системы не могут. Рассмотрим неко­торые примеры:

а) Явление отдачи или отката. Если рассматривать винтовку и пулю как одну систему, то давление пороховых газов при выстреле будет силой внутренней. Эта сила не может изменить суммарное количество движения системы. Но так как пороховые газы, действуя на пулю, сообщают ей некоторое количество движения, направленное вперед, то они одновременно должны сообщить винтовке такое же количество движения в обратном направлении. Это вызовет движение винтовки назад, т.е. так называемую отдачу. Аналогичное явление получается при стрельбе из орудия (откат).

б) Работа   гребного   винта   (пропеллера). Винт сообщает некоторой массе воздуха (или воды) движение вдоль оси винта, отбрасывая эту массу назад. Если рассматривать отбрасываемую массу и самолет (или судно) как одну систему, то силы взаимодействия винта и среды как внутренние не могут изменить суммарное коли­чество движения этой системы. Поэтому при отбрасывании массы воздуха (воды) назад самолет (или судно) получает соответствующую скорость движения вперед, такую, что общее количество движения рассматриваемой системы останется равным нулю, так как оно было нулем до начала движения.

Аналогичный эффект достигается действием весел или гребных колес.

в) Реактивное движение. В реактивном снаряде (ракете) газообразные продукты горения топлива с большой скоростью выбрасываются из отверстия в хвостовой части ракеты (из сопла реактивного двигателя). Действующие при этом силы давления бу­дут силами внутренними, и они не могут изменить суммарное коли­чество движения системы ракета - продукты горения топлива. Но так как вырывающиеся газы имеют известное количество движения, на­правленное назад, то ракета получает при этом соответствующую скорость движения вперед.

Особенно важным частным случаем этой теоремы является закон сохранения момента количества движения, который гласит: если на систему частиц не действуют никакие внешние моменты сил, то ее момент количества движения остается постоянным.

Рассмотрим один очень важный частный случай набора частиц, когда они образуют твердое тело, т. е. объект, который всегда имеет определенную форму и геометрический размер и может только крутиться вокруг какой-то оси. Любая часть такого объекта в любой момент времени расположена одинаковым образом относительно других его частей. Попытаемся теперь найти полный момент количества движения твердого тела. Если масса i-й частицы его равна m_i, а положение ее (x_i, y_i), то задача сводится к определению момента количества движения этой частицы, поскольку полный момент количества движения равен сумме моментов количества движения всех таких частиц, образующих тело. Для движущейся по окружности точки момент количества движения равен, конечно, произведению ее массы на скорость и на расстояние до оси вращения, а скорость в свою очередь равна угловой скорости, умноженной на расстояние до оси:

6

7 Вращательное движение (тоже самое, что и вращение тела с неподвижной осью) — вид механического движения, при котором все точки тела (мы рассматриваем абсолютно твердое тело) описывают окружности, расположенные в параллельных плоскостях.

Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами.

Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси: 

де:

m_i — масса i-й точки,

r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.

Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело

Теорема Штейнера: момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_Cотносительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния dмежду осями:

где:

J_C — известный момент инерции относительно оси, проходящей через центр масс тела;

J — искомый момент инерции относительно параллельной оси;

m — масса тела;

d — расстояние между указанными осями.

Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.

Равноускоренное вращение — вращение с постоянным ускорением.

8 Механическое движение – это изменение положения тела в пространстве относительно других тел.

Например, автомобиль движется по дороге. В автомобиле находятся люди. Люди движутся вместе с автомобилем по дороге. То есть люди перемещаются в пространстве относительно дороги. Но относительно самого автомобиля люди не движутся. В этом проявляется относительность механического движения. Далее кратко рассмотрим основные виды механического движения.

Поступательное движение – это движение тела, при котором все его точки движутся одинаково.

Например, всё тот же автомобиль совершает по дороге поступательное движение. Точнее, поступательное движение совершает только кузов автомобиля, в то время как его колёса совершают вращательное движение.

Вращательное движение – это движение тела вокруг некоторой оси. При таком движении все точки тела совершают движение по окружностям, центром которых является эта ось.

Упоминавшиеся нами колёса совершают вращательное движение вокруг своих осей, и в то же время колёса совершают поступательное движение вместе с кузовом автомобиля. То есть относительно оси колесо совершает вращательное движение, а относительно дороги – поступательное.

Колебательное движение – это периодическое движение, которое совершается поочерёдно в двух противоположных направлениях.

Например, колебательное движение совершает маятник в часах.

Поступательное и вращательное движения – самые простые виды механического движения

Относительность механического движения

Все тела во Вселенной движутся, поэтому не существует тел, которые находятся в абсолютном покое. По той же причине определить движется тело или нет, можно только относительно какого-либо другого тела.

Например, автомобиль движется по дороге. Дорога находится на планете Земля. Дорога неподвижна. Поэтому можно измерить скорость автомобиля относительно неподвижной дороги. Но дорога неподвижна относительно Земли. Однако сама Земля вращается вокруг Солнца. Следовательно, дорога вместе с автомобилем также вращается вокруг Солнца. Следовательно, автомобиль совершает не только поступательное движение, но и вращательное (относительно Солнца). А вот относительно Земли автомобиль совершает только поступательное движение. В этом проявляется относительность механического движения.

Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.

Материальная точка

Во многих случаях размером тела можно пренебречь, так как размеры этого тела малы по сравнению с расстоянием, которое походит это тело, или по сравнению с расстоянием между этим телом и другими телами. Такое тело для упрощения расчетов условно можно считать материальной точкой, имеющей массу этого тела.

Материальная точка – это тело, размерами которого в данных условиях можно пренебречь.

Многократно упоминавшийся нами автомобиль можно принять за материальную точку относительно Земли. Но если человек перемещается внутри этого автомобиля, то пренебрегать размерами автомобиля уже нельзя.

Как правило, решая задачи по физике, рассматривают движение тела как движение материальной точки, и оперируют такими понятиями, как скорость материальной точки, ускорение материальной точки, импульс материальной точки, инерция материальной точки и т.п.

Система отсчёта

Материальная точка движется относительно других тел. Тело, по отношению к которому рассматривается данное механическое движение, называется телом отсчёта. Тело отсчётавыбирают произвольно в зависимости от решаемых задач.

С телом отсчёта связывается система координат, которая представляет из себя точку отсчёта (начало координат). Система координат имеет 1, 2 или 3 оси в зависимости от условий движения. Положение точки на линии (1 ось), плоскости (2 оси) или в пространстве (3 оси) определяют соответственно одной, двумя или тремя координатами. Для определения положения тела в пространстве в любой момент времени также необходимо задать начало отсчёта времени.Система отсчёта – это система координат, тело отсчета, с которым связана система координат, и прибор для измерения времени. Относительно системы отсчёта и рассматривается движение тела. У одного и того же тела относительно разных тел отсчёта в разных системах координат могут быть совершенно различные координаты.

Траектория движения также зависит от выбора системы отсчёта.

Виды систем отсчёта могут быть различными, например, неподвижная система отсчёта, подвижная система отсчёта, инерциальная система отсчёта, неинерциальная система отсчёта.

9 Инерциальная система отсчёта – такая, собственное движение которой не может быть обнаружено никаким механическим опытом. Мысленный эксперимент: «точка, одинокая во всём мире» (изолированная) либо покоится, либо движется прямолинейно и равномерно.

Все системы отсчёта движущиеся относительно исходной прямолинейно, равномерно будут инерциальными. Это позволяет ввести единую декартовую систему координат. Такое пространство называется евклидовым.

Условное соглашение – берут правую систему координат (рис. 1).

 

Время – в классической (нерелятивистской) механике абсолютно, единое для всех систем отсчёта то есть начальный момент – произволен. В отличие релятивистской механики, где применяется принцип относительности. 

Состояние движения системы в момент времени t определяется координатами и скоростями точек в этот момент.

Реальные тела взаимодействуют при этом возникают силы, которые меняют состояние движения системы. Это и есть суть теоретической механики.

Как изучается теоретическая механика?

1. Учение о равновесии совокупности тел некоторой системы отсчёта – раздел статика.

2. Раздел кинематика: часть механики, в которой изучаются зависимости между величинами, характеризующими состояние движения систем, но не рассматриваются причины, вызывающие изменение состояния движения.

После этого рассмотрим влияние сил.

3. Раздел динамика: часть механики, в которой рассматривается влияние сил на состояние движения систем материальных объектов.

Принципы построения основного курса – динамики:

1) в основе – система аксиом (на основе опыта, наблюдений);

2) далее – законы внутренней логики (относительная независимость теории).

Постоянно – безжалостный контроль практики. Признак точной науки – наличие внутренней логики (без неё - набор не связанных рецептов)!

Статикой называется та часть механики, где изучаются условия, которым должны удовлетворять силы, действующие на систему материальных точек, для того чтобы система находилась в равновесии, и условия эквивалентности систем сил.

Будут рассмотрены задачи о равновесии в элементарной статике с применением исключительно геометрических методов, основанных на свойствах векторов. Такой подход применяется в геометрической статике (в отличие от аналитической статики, которая здесь не рассматривается).

Положения различных материальных тел будем относить к системе координат, которую примем за неподвижную.

10

11Положение тела, совершающего плоскопараллельное движение, определяется в любой момент времени положением полюса и углом поворота вокруг полюса (см. § 52). Задачи динамики будут решаться проще всего, если за полюс принять центр масс С тела (рис. 327) и определять положение тела координатами   и углом 

На рис. 327 изображено сечение тела плоскостью, параллельной плоскости движения и проходящей через центр масс С. Пусть на тело действуют внешние силы   лежащие в плоскости этого сечения. Тогда уравнения движения точки С найдем по теореме о движении центра масс

а вращательное движение вокруг центра С будет определяться уравнением (66), так как теорема, из которой получено это уравнение, справедлива и для движения системы вокруг центра масс. В результате, проектируя обе части равенства (70) на координатные оси, получим:

или

Уравнения (71) представляют собой дифференциальные уравнения плоскопараллельного движения твердого тела. С их помощью можно по заданным силам определить закон движения тела или, зная закон движения тела, найти главный вектор и главный момент действующих сил.

При несвободном движении, когда траектория центра масс известна, уравнения движения точки С удобнее составлять в проекциях на касательную   и главную нормаль   к этой траектории. Тогда вместо системы (71) получим:

где   — радиус кривизны траектории центра масс.

Рис. 327

Заметим, что если движение является несвободным, то в правые части уравнений (71) или (72) войдут еще неизвестные реакции связей. Для их определения надо будет составить дополнительные уравнения, отражающие те условия, которые налагаются на движение тела связями (см. задачу 151 и др.). Часто уравнения несвободного движения будут составляться проще с помощью теоремы об изменении кинетической энергии, которой можно воспользоваться вместо одного из уравнений (71) или (72).

Задача 151. Сплошной однородный круговой цилиндр скатывается по наклонной плоскости с углом наклона а (рис. 328). Определить ускорение центра цилиндра и наименьший коэффициент трения   цилиндра о плоскость, при котором возможно качение без скольжения, в двух случаях: 1) пренебрегая сопротивлением качению; 2 учитывая сопротивление качению (коэффициент трения качения k и радиус цилиндра R известны).

Решение. 1. Изображаем действующие на цилиндр силы; силу тяжести   наименьшую силу трения F, при которой возможно качение без скольжения, реакцию N плоскости, приложенную, когда сопротивление качению не учитывается, в точке касания.

12 Пусть точки системы переместились так, что их радиусы-векторы в инерциальной системе отсчета получили приращении . Найдем, как при этом изменилась кинетическая энергия системы . Так как:

то для дифференциала кинетической энергии имеем такое выражение:

Принимая во внимание дифференциальные уравнения (1), перепишем последнее равенство в виде:

Таким образом:

(14)

Последнее равенство выражает теорему об изменении кинетической энергии системы: дифференциал кинетической энергии системы равен элементарной работе всех сил системы.

Подчеркнем, что в отличие от двух рассмотренных выше основных теорем динамики, в теореме об изменении кинетической энергии речь идет о всех силах системы: как внешних, так и внутренних. Тот факт, что силы, с которыми взаимодействуют две точки системы, равны по величине и противоположно направлены, не приводит к равенству нулю работы внутренних сил системы, так как при подсчете работы важны и перемещения точек, а они у двух взаимодействующих точек не обязательно одинаковы. Для твердого тела работа внутренних сил равна нулю, поэтому для него равенство (14) принимает более простой вид

(15)

Проинтегрировав обе части равенства (14) от до , получим интегральную форму теоремы об изменении кинетической энергии

(16)

т. е. приращение кинетической энергии системы за конечное время равно работе всех сил системы, за то же время.

Пусть все силы системы (внешние и внутренние) потенциальны и их потенциал не зависит явно от времени. В этом случае элементарная работа сил системы будет полным дифференциалом

(17)

Из (17) и (14) следует, что тогда .

Сумма кинетической и потенциальной энергий называется полной механической энергией системы. Из последнего равенства следует, что

(18)

т. е. если все силы системы, потенциальны и потенциал не зависит от времени, то при движении, системы ее полная механическая энергия постоянна. Это - закон сохранения механической энергии. Равенство (18) называется интегралом энергии.

Следует иметь в виду, что для справедливости закона сохранения механической энергии требование о том, чтобы все силы системы были потенциальными, не обязательно. Достаточно потребовать, чтобы потенциальными были силы, работа которых на действительном перемещении системы отлична от нуля. Например, работа реакций стационарных идеальных связей равна нулю, и если остальные силы системы потенциальны и потенциал не зависит явно от времени, то для такой системы справедлив закон сохранения механической энергии.

13 Теорема Кенига: Кинетическая энергия системы материальных точек равна сумме кинетической энергии всей массы системы, мысленно сосредоточенной в ее центре масс и движущейся вместе с ним, и кинетической энергии той же системы в ее относительном движении по отношению к поступательно движущейся системе координат с началом в центре масс.