§4.Транспортная задача

В практических приложениях линейного программирования наиболее часто встречается транспортная задача. Это классическая задача линейного программирования о рационализации поставок важнейших видов сельскохозяйственной и промышленной продукции, оптимального планирования грузопотоков, работы различных видов транспорта и др.

Основные понятия. Математическая модель транспортной задачи

Пусть в пунктах производства имеется некоторый однородный груз в количестве соответственно. Этот груз необходимо доставить в пунктов соответственно в количествах . Стоимость перевозки единицы груза из пункта в пункт равна . Требуется спланировать перевозки, чтобы максимально удовлетворить потребности всех потребителей и чтобы суммарные затраты на транспортировку груза были минимальными. Данные транспортной задачи обычно записываются в распределительной таблице.

Если суммарный запас груза равен суммарным потребностям в нем, т.е. , то транспортная задача называется закрытой.

Математическая модель задачи

Целевая функция

.

Система ограничений состоит из двух частей: это ограничение

по ресурсам (поставкам) и по потребностям

Система ограничений закрытой транспортной задачи каноническая, она всегда совместна и состоит из уравнений с переменными.

Свойства системных ограничений

1. Все коэффициенты при переменных равны 1.

2. Каждая переменная входит только в два уравнения.

3. Система ограничений симметрична относительно переменных .

Таким образом, математическая модель транспортной задачи:

Транспортная задача, как любая задача линейного программирования, может быть решена симплекс – методом. Однако такое решение очень громоздко. С учетом особенностей транспортной задачи разработаны более простые методы решения, в которых сохраняются общие приемы метода последовательного улучшения базисного решения (опорного плана):

1) определение исходного базисного решения;

2) оценка этого решения;

3) переход к другому решению путем замещения одной базисной переменной на свободную переменную.

Определение исходного решения может быть осуществлено двумя методами:

метод «северо-западного угла» и метод «наименьшей стоимости».

Методы определения исходного базисного решения

I. Метод «северо-западного угла»

Распределение поставок начинают от первого поставщика к первому потребителю . Если , то весь груз от поставляют , а затем от второго поставщика доставляют недостающий груз потребителю . Оставшийся груз от поставляют второму потребителю и т.д. Если , то полностью удовлетворяют потребности первого потребителя . Оставшийся груз поставляют второму потребителю , стараясь полностью удовлетворить его потребности. В противном случае недостающий груз поставляют от второго поставщика и т.д. Распределение груза производится до тех пор, пока не будет вывезен весь груз, а все потребители не будут полностью удовлетворены. Величину поставки от - ого поставщика к - му потребителю записывают в нижнем правом углу соответствующей клетки. Заполненные клетки в распределительной таблице соответствуют базисным переменным, а свободные клетки – свободным переменным, они перечеркиваются. Заполненных клеток в опорном решении должно быть , так как в системе ограничений такое количество линейно независимых уравнений. Если получим заполненных клеток меньше, чем , то решение будет вырожденным. Чтобы этого не было, искусственно загружают одну (недостающую) клетку нулевым грузом.

Определение. Циклом в матрице (таблице) будем называть ломаную с вершинами в клетках и звеньями, лежащими вдоль строк и столбцов матрицы, удовлетворяющей условиям:

1. ломаная должна быть связной, то есть из любой её вершины можно попасть в любую другую вершину по звеньям ломаной;

2. в каждой вершине ломаной встречаются два звена, одно из которых располагается по строке, другое – по столбцу.

Пример 1.

	50	40	60	70
60	3 50	1 10	4	2
70	5	2 30	3 40	1
90	2	4	5 20	3 70

Опорный план:

.

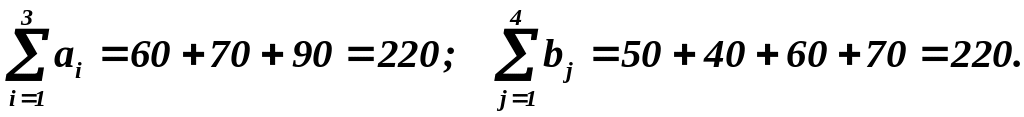Следовательно, закрытая модель транспортной задачи.

Заполненных клеток в данном случае , т.е. решение не вырожденное. Стоимость перевозок при этом плане